토목 공학에서는 점차적으로 다양한 완화 곡선을 사용하여 접선과 원형 원곡선 간 및 곡면이 서로 다른 곡면이 있는 두 원형 원곡선 간의 곡면과 편경사를 점차로 도입하고 있습니다.
다른 접선 및 원곡선에 대한 관계에서 각 완화곡선은 진입 원곡선 또는 진출 원곡선입니다.
완화곡선 설계 및 설정에 가장 일반적으로 사용되는 두 매개변수는 L(완화곡선 길이) 및 R(원형 원곡선의 반지름)입니다.
다음 그림은 완화곡선의 다양한 매개변수를 보여 줍니다.
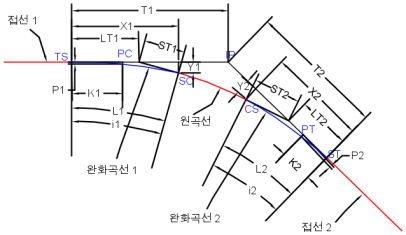
| 완화곡선 매개변수 | 설명 |
| i1 | 완화곡선 L1의 중심 각도(완화곡선 각도)입니다. |
| i2 | 완화곡선 L2의 중심 각도(완화곡선 각도)입니다. |
| T1 | IP에서 TS까지의 총 접선 거리입니다. |
| T2 | IP에서 ST까지의 총 접선 거리입니다. |
| X1 | TS에서 SC의 접선 거리입니다. |
| X2 | ST에서 CS의 접선 거리입니다. |
| Y1 | TS에서 SC의 접선 간격띄우기 거리입니다. |
| Y2 | ST에서 CS의 접선 간격띄우기 거리입니다. |
| P1 | 이동된 PC를 향해 안쪽으로 초기 접선 간격띄우기 |
| P2 | 이동된 PT를 향해 바깥쪽으로 초기 접선 간격띄우기 |
| K1 | TS를 참조한 이동된 PC의 횡좌표입니다. |
| K2 | ST를 참조한 이동된 PT의 횡좌표입니다. |
| LT1 | 긴 접선 완화곡선 입력입니다. |
| LT2 | 긴 접선 완화곡선 출력입니다. |
| ST1 | 짧은 접선 완화곡선 입력입니다. |
| ST2 | 짧은 접선 완화곡선 출력입니다. |
| 기타 완화곡선 매개변수 | |
| A1 | A 값은 완화곡선 길이의 제곱근에 반지름을 곱한 값과 같습니다. 완화곡선의 평평도 측정. |
| A2 | A 값은 완화곡선 길이의 제곱근에 반지름을 곱한 값과 같습니다. 완화곡선의 평평도 측정. |
공식
복합 완화곡선
복합 완화곡선은 반지름이 서로 다른 두 원형 원곡선 간의 변환을 제공합니다. 단순 완화곡선과 마찬가지로, 복합 완화곡선은 곡면 함수의 연속성을 허용하며 편경사에서 평활화 변환을 사용할 수 있습니다.
클로소이드 완화곡선
AutoCAD Civil 3D는 여러 완화곡선 유형을 지원하지만, 가장 일반적으로 사용되는 완화곡선 유형은 클로소이드 완화곡선입니다. 클로소이드 완화곡선은 고속도로와 철도 선로 설계 모두에 사용되는 표준 측면입니다.
스위스 수학자 Leonard Euler가 처음으로 조사한 클로소이드 곡면 함수는 완화곡선이 접선과 만나는 위치에서 곡면이 길이 함수로서 0(영)이 되도록 선택한 선형 함수입니다. 그런 다음 곡면은 완화곡선과 원곡선이 만나는 점에서 인접한 원곡선과 같아질 때까지 선형으로 증가합니다.
접선과 원곡선이 곡면 점(PC)에서 연속성을 제공하는 것처럼 그러한 선형은 위치 함수와 첫 번째 도함수(로컬 방위각)의 연속성을 제공합니다. 그러나 단순 원곡선과는 다르게 고속에서 점점 더 중요해지고 있는 두 번째 도함수(로컬 곡면)의 연속성도 유지합니다.
공식
클로소이드 완화곡선은 다음과 같이 설명될 수 있습니다. 
완화곡선의 평평도: 
완화곡선에 대응되는 총 각도: 
접선-완화곡선 점에서 완화곡선-원곡선 점의 접선 거리:
접선 -완화곡선 점에서 완화곡선-원곡선 점의 접선 간격띄우기 거리:
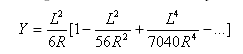
Bloss 완화곡선
클로소이드를 사용하는 대신 5번째 각도의 포물선이 있는 Bloss 완화곡선을 변환으로 사용할 수 있습니다. 이 완화곡선은 클로스이드에 비해 이동 P가 작기 때문에 더 긴 변환과 완화곡선 확장(K)을 갖는다는 이점이 있습니다. 이 요인은 난간 설계에서 중요합니다.
공식
Bloss 완화곡선은 다음과 같이 설명될 수 있습니다.
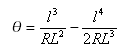
기타 주요 표현식:
접선-완화곡선 점에서 완화곡선-원곡선 점의 접선 거리:
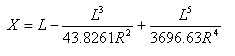
접선 -완화곡선 점에서 완화곡선-원곡선 점의 접선 간격띄우기 거리:
사인 원곡선
이러한 원곡선은 곡면의 일정한 방위각을 나타내며 0도에서 90도 사이의 접선 편각 변환에 적용할 수 있습니다. 그러나 사인 원곡선은 완화곡선보다 경사가 급해 평면으로 만들어 측량하기 어렵기 때문에 광범위하게 사용되지는 않습니다.
공식
사인 원곡선은 다음과 같이 설명될 수 있습니다.
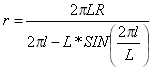
여기서 r는 지정된 점에서 곡면의 반지름입니다.
사인 반파장 감소 접선 원곡선
이 계산식은 일본에서 철도를 설계하는 데 일반적으로 사용됩니다. 이 원곡선은 차체 역학과 관련하여 낮은 편각에 대한 곡면 변경에서 효과적인 변환이 필요한 상황에 유용합니다.
공식
사인 반파장 감소 접선 원곡선은 다음과 같이 설명될 수 있습니다.
및 x가 원곡선의 시작 위치에서 임의의 점까지의 거리가 확장된 처음 접선을 따라 측정됩니다. X는 완화 곡선 끝의 전체 X를 나타냅니다.
기타 주요 표현식:
접선-완화곡선 점에서 완화곡선-원곡선 점의 접선 거리:
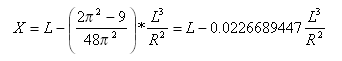
접선 -완화곡선 점에서 완화곡선-원곡선 점의 접선 간격띄우기 거리:
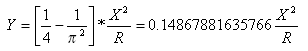
3차 포물선
3차 포물선은 철도 및 고속도로 설계 시 널리 사용되는 3차 포물선보다 느리게 수렴됩니다.
공식
3차 포물선의 최소 반지름
3차 포물선의 모든 점에서 반지름:
3차 포물선에서 최소 r를 얻을 수 있는 식:
따라서 
입니다.
3차 포물선 반지름은 24도, 5분, 41초에 무한대에서 으로 줄어들고 그 이후 다시 증가합니다. 이 때 편각이 24도보다 큰 경우 3차 포물선은 사용할 수 없습니다.
입방(JP)
이 변환은 일본의 요구사항에 맞게 개발되었습니다. 작은 편각 또는 큰 반지름을 수용해야 하는 경우 사용할 수 있도록 몇 개의 클로소이드 근사값이 개발되었습니다. 이러한 근사값 중 하나로 일본에서 설계에 사용되는 입방(JP)이 있습니다.
공식
입방(JP)은 다음과 같이 설명할 수 있습니다.
여기서 X는 접선-완화곡선 점에서 완화곡선-원곡선 점의 접선 거리입니다.
또한 이 공식은 다음과 같이 표현될 수 있습니다.
여기서 
은 완화곡선의 중심 각도입니다(그림의 i1 및 i2).
기타 주요 표현식:
접선-완화곡선 점에서 완화곡선-원곡선 점의 접선 거리:
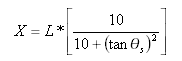
접선 -완화곡선 점에서 완화곡선-원곡선 점의 접선 간격띄우기 거리:
NSW 3차 포물선
이것은 뉴사우스웨일스(호주) 표준의 요구사항을 충족하도록 수정된 3차 포물선의 유형입니다.
공식
NSW 3차 포물선을 다음과 같이 표현할 수 있습니다.
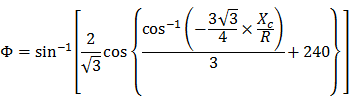
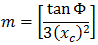
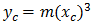
여기서 각 항목은 다음과 같습니다.
Φ = R의 최종 반지름 선과 초기 접선의 수직선 간의 각도
R = 원곡선 반지름
Xc = 지정된 완화곡선의 전체 X
4차(Schramm) 포물선
4차(Schramm) 포물선에는 수직 가속도의 낮은 값이 포함되어 있습니다. 이러한 포물선에는 원곡선 길이 함수에 따라 반지름이 변하는 두 개의 2도 포물선이 포함되어 있습니다.
간단한 원곡선 공식
첫 번째 포물선의 곡면:
의 경우 
두 번째 포물선의 곡면:
의 경우 
이러한 원곡선은 완화곡선의 사용자 정의 길이(L)에 의해 지정됩니다.
복합 원곡선 공식
첫 번째 포물선의 곡면:
의 경우 
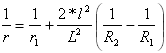
두 번째 포물선의 곡면:
의 경우 