智能粘合是一种即使网格不匹配也会连接相邻部件上的节点的方法。智能粘合适用于线性分析和热分析,可在“常规接触设置”对话框的“智能粘合”选项卡内启用它。要访问此对话框,请双击浏览器中的“常规接触设置”标题(树视图),或在该标题上单击鼠标右键,然后选择“编辑设置”。可使用以下智能粘合选项:
- 禁用智能粘合
- 粗粘合到细网格
- 细粘合到粗网格
以下部分为选择合适的“智能粘合”选项提供指导。
智能粘合旨在连接不重合的节点。需要容差来控制连接节点之间的相隔距离。启用智能粘合后,可通过双击浏览器中的“粘合”或“焊接”接触对标题(或在该标题上单击鼠标右键)并选择“编辑设置”,来访问容差。可以从默认接触标题或明确定义的接触对访问智能粘合容差选项。
智能粘合公差类型:有两个选项可用于智能粘合容差类型,如下所示:
- 网格大小的分数:使用“值”字段中的输入乘以网格大小以创建尺寸。在一个表面的此距离内的另一个表面上的节点将被粘合。(网格大小基于节点位置的平均单元大小。)
- 绝对大小:使用“值”字段中的尺寸将节点匹配到相连表面。
软件将根据相对网格尺寸和指定的“智能粘合”模式来确定将哪些表面节点粘合到相邻表面。此过程不依赖于浏览器中显示的接触条目顺序。但是,相应容差值可能会受“智能粘合”模式影响。细网格上的节点与粗网格上最近节点之间的距离可能明显不同于粗网格上的节点与细网格上最近节点之间的距离。希望随着“智能粘合”模式之间的差异的进一步说明,此概念能变得更清晰。
“智能粘合”选项适用于“粘合”接触和“焊接”接触。使用原生 Simulation Mechanical (SimMech) 求解器时,其他接触类型(“自由”除外)都需要节点匹配。有关其他信息,请参见接触类型页面。
- Autodesk Simulation Mechanical 中称为粘合接触的定义等同于 Nastran 中的焊接接触。使用 Nastran 求解器时,将沿焊接接触的整个接触表面进行粘合。此行为不同于使用 SimMech 求解器时的焊接接触,在这种情况下,仅粘合接触表面的周界(模拟围绕部件接触面周界的焊道效果)。
- 如果同一网格将用于其他分析但另一个分析不支持智能粘合(例如使用焊接接触时的非线性分析),请不要使用智能粘合。此外,如果接触类型将更改为不支持智能粘合的类型(例如从粘合接触更改为表面接触),则应为这两个分析匹配网格。
智能粘合功能
智能粘合将载荷从一个部件上的节点传输到另一个部件上的相邻节点,方法是通过使用方程将部件的自由度(对于应力分析为位移,对于热传递为温度)关联到一起。该关联可通过使用与多点约束 (MPC) 相同的方法完成。在应力分析中,将为块体和二维单元连接平动。对于板对板单元,将连接平动和转动。有关示例,请参见图 1。
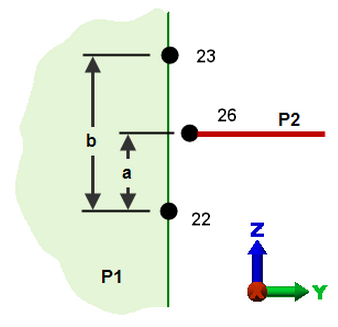
请考虑部件 A/表面 C 和部件 B/表面 D 之间的接触对。由于表面 D 上的节点可能会连接到表面 D 区域外的表面 B 上的节点,因此智能粘合可在比实际接触区域更大的区域上将载荷从部件 C 分配到部件 A。当然,载荷的扩散度数取决于网格大小。请参见图 1(a)。
|
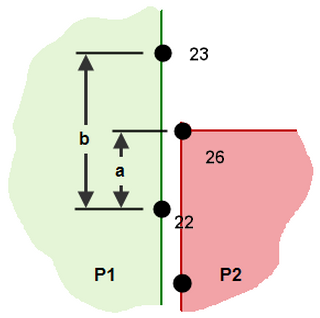
TX26 = TX22 + (a/b)(TX23-TX22) TY26 = TY22 + (a/b)(TY23-TY22) TZ26 = TZ22 + (a/b)(TZ23-TZ22) T 为指定节点处的 X、Y 或 Z 方向的平动。 |
|
(a) 实体 (P1) 对实体 (P2) 连接,采用智能粘合,应力分析。 由于部件 2 在节点 22 和 23 处连接到部件 1,将在大于部件 1 和 2 之间接触面的区域上传递载荷。此近似值更精确,因为部件 1 上的网格尺寸减小。 |
|
|
TY26 = TY22 + (a/b)(TY23-TY22) TZ26 = TZ22 + (a/b)(TZ23-TZ22) RX26= 0 R 为指定节点处的 X、Y 或 Z 方向的转动。 |
|
(b) 板 (P2) 对实体 (P1) 连接,采用智能粘合,应力分析。 (为了简单明了,考虑使用二维视图) |
|

|
T26 = T22 + (a/b)(T23-T22) T 为指定节点处的温度。 |
| (c) 实体对实体连接,采用智能粘合,热传递分析。 | |
| 图 1:智能粘合示例 | |
有关中节点的提示
使用智能粘合将部件 A(需要更精确结果的部件)上的中节点与部件 B(无中节点,无需高精度的部件)上的角节点连接。
|
|
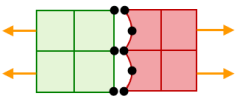
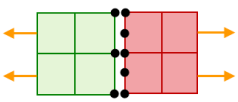
| 未使用智能粘合的情况下,右侧部件中的中节点能够脱离左侧部件的面。(为清晰起见,仅显示了接触面上的节点。) | 使用智能念合,中节点被粘合到左侧部件的面上。因此,中节点无法脱离。(为清晰起见,显示的部件具有微小的间隙。) |
| 图 2:粘合中节点 | |
有关旧版模型的说明
在引入智能粘合之前创建的模型可能依赖不匹配的网格创建自由表面,即使接触类型设置为粘合。如果重新分析此类模型,则不得启用智能粘合;否则,此类表面此时将相当于已粘合。请参见图 3。(默认情况下,将为旧版模型禁用智能粘合。)
|
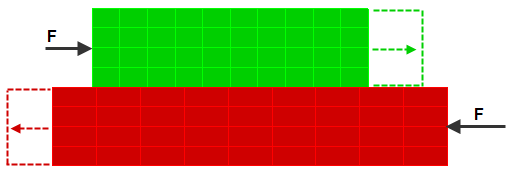
(a) 在智能粘合之前,由于节点不匹配,部件未粘合。(实际上,任何类型的接触都不起作用,因为节点不匹配。)切向力 F 使部件能够分离。 |
|
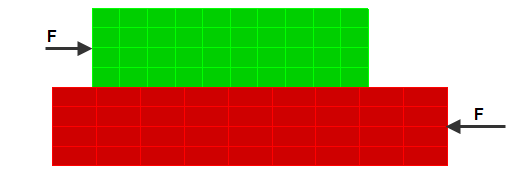
(b) 如果在具有智能粘合功能的软件中打开相同模型,且如果接触类型为粘合并启用智能粘合,则即使节点不匹配也将粘合部件。因此,部件不会分离。避免出现此问题,禁用“启用智能粘合/焊接接触”选项,或将相应表面的接触类型设置为“自由/无接触”。 |
| 图 3:具有不匹配网格的自由接触(旧版模型) |
点焊是其中某些节点不匹配且您不想粘合这些节点的全等表面的示例。
选择最佳智能粘合选项
上述讨论(图 1)暗示部件 2 上的节点连接到部件 1 上的节点。您不具有此级别的控制。不过,您可以指定具有粗网格的表面上的节点是否连接到细网格一侧,反之亦然。除用户指定的“智能粘合”选项外,软件会决定哪个表面为细网格,哪个为粗网格。请注意,需考虑接触表面上的所有单元;一部分接触表面的网格大小不是粗细的决定因素。仅使用相对于相对表面上节点处于指定容差范围(见上文)内的节点。接触区域外的节点不用于确定粗细。例如,如果在部件 1 和 4 之间定义一个显式接触对,将计数部件 1 和 4 之间接触的所有节点,不论接触是在一个面还是在多个面。具有较少接触节点的部件成为粗网格。(“默认”接触设置也是如此;两个部件之间的所有接触节点均用于确定网格为细还是粗。)对于定义部件/表面和部件/表面之间的接触的接触对,使用在指定表面上接触的节点确定网格是细还是粗。
选择所使用的智能粘合类型(“粗粘合到细网格”或“细粘合到粗网格”)时,考虑两个部件之间应该发生的情况很有帮助。如图 4 至 7 中所示。
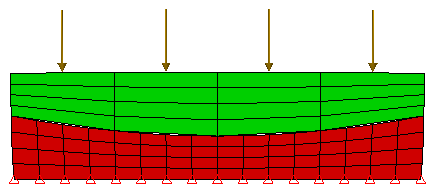
对于接触面遇到纯压缩的应力分析,接触面上的所有节点均应发生相同的量变形。因此,选择“细粘合到粗网格”将提供更精确的结果。请参见图 4。
|
(a) 模型。简单的压缩模型。 |
|
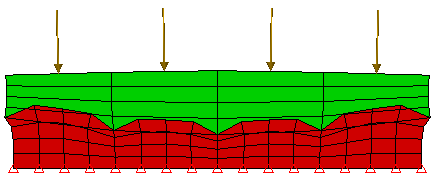
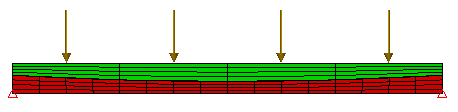
(b) 不正确。当使用“粗粘合到细网格”智能粘合时,仅强制粗网格上的节点遵循细网格的位移。因此,细网格上的内部节点可自由独立移动。如该放大的位移图中所示,细网格位移错误。 |
|
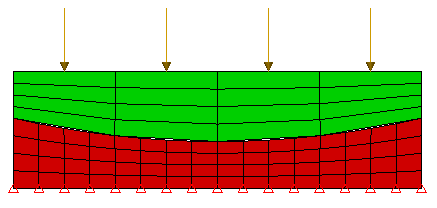
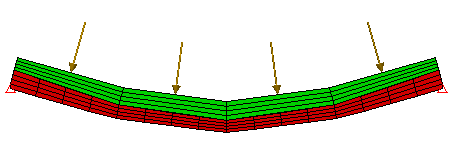
(c) 正确。当使用“细粘合到粗网格”智能粘合时,将强制细网格上的节点遵循粗网格的位移。这两个网格均根据需要变形(尽管强制细网格在粗单元节点之间的节点上线性位移。这可能会导致某些误差)。此处显示了 (b) 中使用的相同的放大位移比例。 |
| 图 4:纯压缩下的应力分析 |
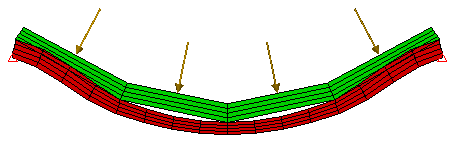
对于接触面遇到弯曲的应力分析,必须允许更精细网格表面上的节点独立于较粗网格上的节点移动;即,两组节点应位移以便创建相同的曲率半径。因此,选择“粗粘合到细网格”将提供更精确的结果。请参见图 5。
|
(a) 模型。简单的弯曲模型。 |
|
(b) 不正确。当使用“细粘合到粗网格”智能粘合时,将强制细网格上的节点遵循粗网格的位移。通过强制细网格弯曲成粗网格产生的相同曲率,位移结果会不太精确。由于底部部件中的每组 4 个单元扭结或斜率突然改变,应力结果尤其会表现出较高的应力。此处显示了 (c) 中使用的相同的放大位移比例,因此此变形明显更小。 |
|
(c) 正确。当使用“粗粘合到细网格”智能粘合时,仅强制粗网格上的节点遵循细网格的位移。因此,细网格上的内部节点可自由独立移动。尽管由于底部部件从顶部部件分离(此处进行了很大程度地放大以更好地显示形状)而使底部部件的位移可能看起来不正确,但两个部件遵循适当曲率的情况表明这些结果更加精确。 |
| 图 5:纯弯曲下的应力分析 |
在热传递分析中,热量应持续从细网格流入粗网格。因此,选择“细粘合到粗网格”将提供更精确的结果。请参见图 6。类似的原理适用于静电分析。
|
(a) 模型。一个简单的两部分模型,底部表面暴露于热环境,顶部表面暴露于冷环境。因为这两个部件具有几乎相同的宽度,此二维模型表示一维热传递。 |
|
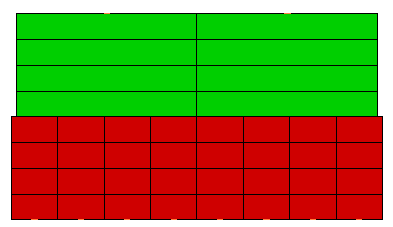
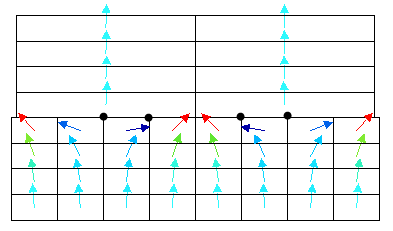
(b) 不正确。当使用“粗粘合到细网格”智能粘合时,仅强制粗网格上的节点遵循细网格的温度。因此,细网格上的内部节点(显示为圆点)未连接至顶部部件。这些会对热流形成堵塞(如每个单元中间的箭头所示)。热流必须从堵塞的节点侧面流至顶部部件;这会形成不太精确的温度曲线。 |
|
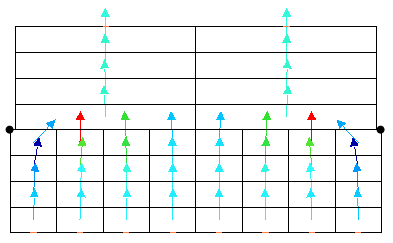
(c) 正确。当使用“细粘合到粗网格”智能粘合时,将强制细网格上的节点遵循粗网格的温度。因此,只有两个外部节点(显示为圆点)未连接至顶部部件。在热流量堵塞降低的情况下,热流量矢量更接近平行(因为它们应用于一维热传递)。因此,会提供更精确的温度曲线。 |
|
图 6:热传递分析 |
选择智能粘合类型的另一个考虑因素是所选表面上需要存在与相对的表面实际相匹配的节点。请参见图 7。
|
“粗粘合到细网格”智能粘合与“细粘合到粗网格”智能粘合。如果通过选择“粗粘合到细网格”仅将粗(底部,红色)部件上的节点粘合到细(顶部,绿色)部件上,则将仅粘合一个节点(右侧的节点)。由于粗网格上的节点不会接触到另一个部件,因此不会粘合其他节点。如果这是应力分析,则顶部部件可能不具备静态稳定性。要使此示例获得预期效果,更好的选择是“细粘合到粗网格”智能粘合。由于顶部部件上的所有节点都接触底部部件,因此它们将全部将粘合到底部部件上的节点上。 |
| 图 7:粘合显著不同的网格尺寸 |
请记住,智能粘合近似于在两个部件的边界传递载荷。在应力分析中,会保持位移的连续性。其他量(如力、应力、位移的导数)不是连续的。因此,进行智能粘合的边界处的结果可能不精确,具体取决于相对网格密度。然而,相对于智能粘合产生的效果(若有),远离边界的结果应该是精确的。如果部件间的边界处需要精确的结果,则不应使用智能粘合;而是应匹配网格。
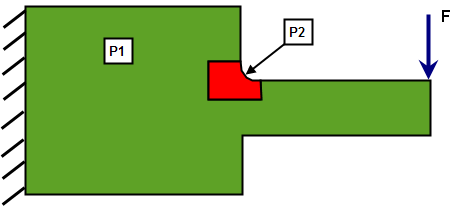
智能粘合的一个优点是执行假设分析并更改一个部件上的网格,而无需对整个模型重新执行网格划分。智能粘合将保持接触面处的连接,即使网格可能未对齐。请参见图 8。
|
|
图 8:智能粘合的使用示例。 通过更改部件 2 [P2] 上的网格可以执行网格敏感度分析,而无需对整个模型重新执行网格划分。部件 2 的几何体也可更改,如比较倒角与较大半径圆角与较小半径圆角。 |
多点约束求解方法
默认情况下,智能粘合使用压缩方法对分析求解。如果发现分析未收敛或未按预期执行,则可尝试使用不同的求解方法(请参见多点约束)。依次单击“设置” “约束”
“约束” “多点约束”,并从可用“求解方法”选项中选择。
“多点约束”,并从可用“求解方法”选项中选择。
如果使用“罚函数方法”,则解的精确度将由“罚函数乘子”字段控制。将刚度应用于 MPC 方程,并将此刚度添加到法向刚度矩阵中。罚函数求解期间会将罚函数乘子乘以模型中的最大对角线刚度。乘子为 0 表示部件未连接,乘子无限大表示部件之间完美粘合。遗憾的是,无限刚度在数值求解中不可接受,也不是必需的。建议使用 104 到 106 之间的值。但是,某些分析可能会产生最大至最小刚度警告(“最大/最小刚度”)或在罚函数乘子过大时无法找到求解。
为判断求解的精度,总结文件包括一个带满意度因子的行。值 100% 表示 MPC 方程(如图 1 中)完全令人满意。任何小于 100% 的值都表示部件存在某些分离。低于特定百分比的值不表示求解就是错误的。根据经验来判断满意度何时表示不可接受的结果。
- 您在“定义多点约束”对话框中选择的求解方法将成为含 MPC 的所有特征将使用的方法。这些特征包括但不限于:循环对称、无摩擦约束、智能粘合和用户定义的 MPC。例如,如果要使用“罚函数方法”对涉及智能粘合或其他 MPC 相关特征的所有分析求解,则可在“定义多点约束”对话框中选择“罚函数方法”,来替代默认的压缩方法。
- 智能粘合适用于块体、二维、膜和板单元之间的接触。涉及其他单元类型的粘合接触需要节点匹配,且不受智能粘合设置的影响。