1D-Toleranzstapelanalyse
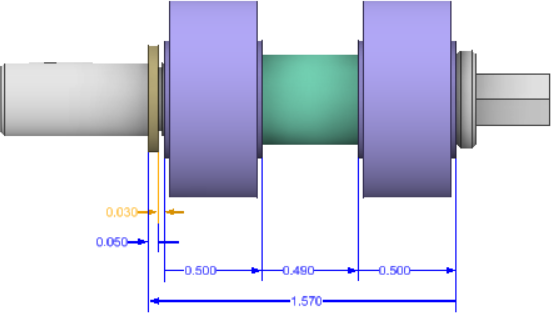
- Gleichzeitige Verwaltung aller Produktanforderungen
- Verwendung gemeinsamer Bemaßungen und Toleranzen für jedes Bauteil, das in mehreren Stapeln enthalten ist
- Präzise Berechnung der Effekte geometrischer Toleranzen
- Automatische Berücksichtigung der Effekte der Zwischenräume um Schrauben und Stifte, was zu einer Baugruppenverschiebung und Abweichung bei der Platzierung eines Bauteils relativ zu einem anderen führt
- Präzise Berechnung der statistischen Ergebnisse
Inventor Tolerance Analysis ersetzt die Tabellenmethode, indem diese und viele andere gängige Toleranzstapelaufgaben automatisiert werden.
Grundlagen der Toleranzstapelanalyse
Die folgenden Informationen erläutern, warum die Toleranzanalyse wichtig ist, es werden die Unterschiede zwischen 1D-, 2D- und 3D-Analyseproblemen sowie die verschiedenen Arten von Toleranzanalysen dargestellt. Wenn Sie mit der Ausführung von Toleranzstapeln vertraut sind, können Sie diesen Abschnitt überspringen und direkt mit dem Definieren und Bearbeiten von Toleranzstapeln fortfahren.
Wenn Sie ein Bauteil in einem CAD-System entwerfen, ist dies eine perfekte Entsprechung des Bauteils. In der Realität entstehen bei der Herstellung eines Bauteils jedoch geringe Unterschiede bei den einzelnen Bauteilen. Der Zweck der Toleranzauslegung liegt darin, die zulässige Abweichung bei jedem Bauteil zu berücksichtigen, um zu ermitteln, ob die technischen Anforderungen erfüllt werden, wenn die Bauteile zusammengebaut werden.
Um zu bestimmen, wie viel Toleranz zulässig ist, müssen Sie die Kumulation bzw. den Stapel der Abweichungen bei den einzelnen Bemaßungen berücksichtigen. Maßabweichungen in den Bauteilen führen zusammengenommen zu Abweichungen bei wichtigen Abständen, in der Regel zwischen zwei unterschiedlichen Bauteilen einer Baugruppe. Für jeden wichtigen Abstand müssen Sie ermitteln, welcher Wertebereich zulässig ist, sodass das System weiterhin wie gewünscht funktioniert.
Die Toleranzstapelanalysis bietet eine Möglichkeit zur Veranschaulichung der Beziehung zwischen Maßabweichungen und funktionalen Anforderungen.
Inventor Tolerance Analysis kann eindimensionale (1D) Stapelprobleme lösen, jedoch keine 2D- oder 3D-Stapelprobleme. In vielen Fällen können 2D- oder 3D-Einflüsse auf den definierten Stapel erkannt werden, und es wird eine Warnmeldung ausgegeben. Im folgenden Abschnitt werden die Unterschiede zwischen 1D-, 2D- und 3D-Stapeln erläutert, damit Sie verstehen können, warum die Meldung angezeigt wird.
Bei einem 1D-Toleranzstapel wirken der analysierte Abstand und alle Bemaßungen, die zur Abstandsabweichung beitragen, in derselben linearen Richtung. Lineare Abweichungen von Flächen auf beiden Seiten der Stapelrichtung werden berücksichtigt; Winkelabweichungen der Flächen relativ zueinander werden nicht berücksichtigt. Manchmal werden die Effekte von Winkelabweichungen übergangen und die Analyse wird als 1D-Analyse betrachtet. Wenn jedoch erhebliche Unterschiede in der Größe der Flächen im Stapel vorhanden sind, kann eine Winkelabweichung auf kleineren Flächen größere Auswirkungen auf die Kanten der größeren Flächen haben. Wenn größere Flächen der Ausrichtung der kleineren Flächen folgen, ist deren Bewegung in der Richtung der Analyse größer, als die einfache Translation der Flächen es zulassen würde. Sie werden von Tolerance Analysis gewarnt, wenn dieses Szenario (und Szenarien mit ähnlichen Effekten) erkannt wird.
Bei einem 1D-Problem beträgt die Empfindlichkeit des gesamten Stapelabstands für die einzelnen einbezogenen Bemaßungen normalerweise entweder 1.0 oder -1.0 für Standardbemaßungen. Die Empfindlichkeit für Größenbemaßungen, beispielsweise Durchmesser oder Breite, kann 0.5 oder -0.5 betragen.
Bei einem 2D-Toleranzstapel können der analysierte Abstand und alle Bemaßungen, die zur Abweichung von diesem Abstand beitragen, in einer einzelnen Ebene dargestellt werden. Ein 3D-Toleranzstapel kann einbezogene Bemaßungen in allen Richtungen umfassen. Beide beinhalten in der Regel komplexe trigonometrische Berechnungen zur Ermittlung der Empfindlichkeit der Messung für jede Bemaßung in der Baugruppe.
Toleranzanalysetypen
Inventor Tolerance Analysis unterstützt die Worst-Case-, die allgemeine statistische und die RSS-Analysemethode (Root Sum of Squares, Quadratmittel). RSS ist eine spezielle Form der statistischen Analysemethode und wird nach dem Abschnitt Statistisch beschrieben.
Die Worst-Case-Toleranzanalyse ist die herkömmliche Art der Toleranzstapelberechnung. Die einzelnen Variablen werden alle entweder am maximalen oder am minimalen Grenzwert platziert, um den Stapelabstand so groß oder so klein wie möglich zu machen.
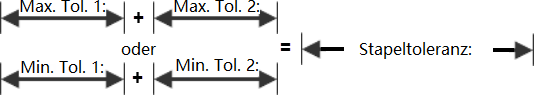
Bei der Worst-Case-Methode wird die Verteilung der einzelnen Variablen nicht berücksichtigt. Es wird stattdessen davon ausgegangen, dass alle Bauteile am äußersten Grenzwert des Akzeptanzbereichs produziert wurden, wenn sie zusammengebaut werden Bei dieser Methode werden die absoluten oberen und unteren Grenzwerte des Stapelabstands, die erreicht werden können, prognostiziert.
Eine Entwicklung auf Basis der Worst-Case-Toleranzanforderungen bedeutet, dass alle hergestellten Bauteile bis zu den äußersten Grenzwerten, jedoch nicht darüber hinaus, zusammengebaut werden können und ordnungsgemäß funktionieren. Der große Nachteil bei der Worst-Case-Methode besteht darin, dass sie häufig sehr strikte Toleranzen für einzelne Komponenten erfordert. Dies kann zu kostspieligen Produktions- und Prüfprozessen und hohen Ausschussraten führen.
Die Zuweisung von Toleranzen, die die Anforderungen der Worst-Case-Analysemethode erfüllen, wird häufig für wichtige mechanische Schnittstellen und Schnittstellen für Ersatzteile angewendet. Wenn die Worst-Case-Toleranzmethode nicht aufgrund des Vertrags erforderlich ist, kann eine ordnungsgemäß angewendete statistische Toleranzmethode zulässige Baugruppenergebnisse mit erhöhten Komponententoleranzen und geringeren Herstellungskosten sicherstellen.
Die statistische Analysemethode nutzt die Prinzipien der Statistik, um die Komponententoleranzen zu lockern, ohne Kompromisse bei der Qualität einzugehen. Bei jeder einbezogenen Bemaßung wird von einer statistischen Verteilung ausgegangen. Diese Verteilungen werden kombiniert, um die Verteilung des Stapelabstands der Baugruppe zu prognostizieren. Bei der statistischen Analyse wird eine Verteilung des Stapelabstands anstatt der äußersten Grenzwerte wie bei der Worst-Case-Methode prognostiziert. Statistische Analyse bietet mehr Flexibilität bei der Planung auf jeder Qualitätsstufe und nicht nur bei 100 %. Statistische Analyse unterscheidet sich von der RSS-Methode, da hier nicht davon ausgegangen wird, dass die Qualitätsstufe der Baugruppe gleich der Qualitätsstufe des Bauteils sein muss.
Die Standardabweichung, die für die Normalverteilung jeder Bemaßung berechnet wird, wird anhand der folgenden Cp-Formel berechnet:

Lösung für Standardabweichungsergebnisse:
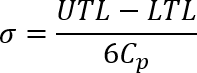
Die häufigste Annahme bei Cp=1.0 hat ihren Ursprung in der Annahme eines Fertigungsprozesses, bei dem die definierten Toleranzen bei +/- 3 Standardabweichungen vom Mittelpunkt der Toleranzzone platziert werden, was als Mittelwert betrachtet wird, sodass die Wahrscheinlichkeit, dass ein Bauteil die erforderlichen Toleranzen erfüllt, bei 99,7 % liegt. Für alle statistischen Analysen geht Tolerance Analysis davon aus, dass sich die Fertigung auf den Mittelpunkt des Toleranzbereichs konzentriert, daher wird als Mittelwert der Mittelpunkt des Toleranzbereichs angenommen.
Bei der RSS-Analyse (Root Sum of Squares, Quadratmittel) werden die Prinzipien der oben erläuterten allgemeinen statistischen Analysemethode genutzt, allerdings werden einige vereinfachende Annahmen angewendet, um Berechnungen mit Toleranzen anstelle von Standardabweichungen zu ermöglichen. Eine der wichtigsten Annahmen besteht darin, dass die Verhältnisse der einzelnen Toleranzen zu den zugehörigen Standardabweichungen an den Bemaßungen und das Stapelergebnis identisch sind. Bei der RSS-Analyse geht Tolerance Analysis von einem Cp-Wert von 1.0 für alle Bemaßungen sowie für die resultierenden Stapelgrenzwerte aus.