Informationen zu Übergangsbogendefinitionen

In seiner Beziehung zu anderen Tangenten und Bogen ist jeder Übergangsbogen entweder ein Inwärtsbogen oder ein Auswärtsbogen.

Die zwei von Ingenieuren beim Entwurf eines Übergangsbogens am häufigsten verwendeten Parameter sind L (Übergangsbogenlänge) und R (Radius des Kreisbogens).

Die folgende Abbildung zeigt die verschiedenen Parameter eines Übergangsbogens:

Übergangsbogenparameter	Beschreibung
i1	Der zentrale Winkel des Übergangsbogens L1, der dem Übergangsbogenwinkel entspricht.
i2	Der zentrale Winkel des Übergangsbogens L2, der dem Übergangsbogenwinkel entspricht.
T1	Die tangentiale Gesamtentfernung zwischen PI und TS.
T2	Die tangentiale Gesamtentfernung zwischen PI und ST.
X1	Die tangentiale Entfernung bei SC von TS.
X2	Die tangentiale Entfernung bei CS von ST.
Y1	Die tangentiale Versatzentfernung bei SC von TS.
Y2	Die tangentiale Versatzentfernung bei CS von ST.
P1	Der Versatz der Anfangstangente in den PC des versetzten Bogens.
P2	Der Versatz der Anfangstangente aus dem PT des versetzten Bogens.
K1	Die Abszisse des versetzten PC bezogen auf den TS.
K2	Die Abszisse des versetzten PT bezogen auf den ST.
LT1	Der lange tangentiale Übergangsbogen vorne.
LT2	Der lange tangentiale Übergangsbogen hinten.
ST1	Der kurze tangentiale Übergangsbogen vorne.
ST2	Der kurze tangentiale Übergangsbogen hinten.
	Sonstige Übergangsbogenparameter
A1	Der Wert A entspricht der Quadratwurzel aus der Übergangsbogenlänge multipliziert mit dem Radius. Dient zur Messung der Flachheit des Übergangsbogens.
A2	Der Wert A entspricht der Quadratwurzel aus der Übergangsbogenlänge multipliziert mit dem Radius. Dient zur Messung der Flachheit des Übergangsbogens.

Formel

Zusammengesetzter Übergangsbogen

Zusammengesetzte Übergangsbogen ermöglichen einen Übergang zwischen zwei Kreisbogen mit unterschiedlichen Radien. Ebenso wie beim einfachen Übergangsbogen wird dadurch die Kontinuität der Krümmungsfunktion gewährleistet und die Möglichkeit gegeben, einen Übergang in eine Querneigung einzufügen.

Klothoide-Übergangsbogen

Autodesk Civil 3D unterstützt verschiedene Arten von Übergangsbogen. Die Klothoide ist jedoch die am häufigsten verwendete Art des Übergangsbogens. Der Cornu-Übergangsbogen wird weltweit in der Spurkonstruktion von Straßen und Eisenbahnschienen verwendet.

Der Schweizer Mathematiker Leonard Euler fand als Erster heraus, dass die Krümmungsfunktion der Klothoide eine lineare Funktion ist, bei der die Krümmung als Funktion der Länge, an der der Übergangsbogen die Tangente berührt, dem Wert null (0) entspricht. Danach steigt die Krümmung linear an, bis sie am Berührungspunkt von Übergangsbogen und Bogen mit dem Krümmungsgrad des angrenzenden Bogens übereinstimmt.

Eine derartige Achse gewährleistet die Kontinuität der Positionsfunktion und deren erster Ableitung (lokaler Azimut), ebenso wie bei einer Tangente und einem Bogen am Kurvenpunkt (Pc). Im Gegensatz zum einfachen Bogen wird jedoch auch die Kontinuität der zweiten Ableitung (lokale Krümmung) gewährleistet, was besonders bei hohen Geschwindigkeiten von Bedeutung ist.

Formel

Klothoide können folgendermaßen ausgedrückt werden:

Ebenheit des Übergangsbogens:

Gesamtwinkel von Übergangsbogen:

Tangentenabstand am Punkt Übergangsbogen-Bogen zum Punkt Tangente-Übergangsbogen:

Tangentenversatzabstand am Punkt Übergangsbogen-Bogen vom Punkt Tangente-Übergangsbogen:

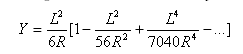
Blossbogen-Übergangsbogen

Anstelle der Klothoide kann die Bloss-Spirale mit der Parabel fünften Grades als Übergang verwendet werden. Dieser Übergangsbogen hat gegenüber der Klothoide den Vorteil, dass der Versatz P kleiner und der Übergang daher länger sowie die Spiralverlängerung (K) größer ist. Dies ist ein wichtiger Faktor bei der Konstruktion von Eisenbahnschienen.

Formel

Blossbogen-Übergangsbogen können folgendermaßen ausgedrückt werden:

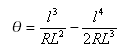
Andere wichtige Ausdrücke:

Tangentenabstand am Punkt Übergangsbogen-Bogen vom Punkt Tangente-Übergangsbogen:

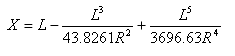
Tangentenversatzabstand am Punkt Übergangsbogen-Bogen zum Punkt Tangente-Übergangsbogen:

Sinusoide

Diese Bogen stellen einen konsistenten Krümmungsverlauf dar und können Übergänge zwischen 0 und 90 Grad an Tangentenabschrägungen aufweisen. Sinusoide werden jedoch nicht häufig verwendet, weil ihr Verlauf steiler als der von Übergangsbogen ist. Dies erschwert das Tabellarisieren und Abstecken.

Formel

Sinusoide können wie folgt ausgedrückt werden:

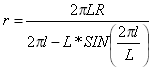
wobei r der Radius der Krümmung an einem beliebigen Punkt ist.

Gedämpfte sinusförmige Halbwellen-Tangente

Diese Art der Gleichung wird für gewöhnlich in Japan beim Entwurf von Eisenbahnschienen verwendet. Dieser Bogen wird in Situationen verwendet, in denen Sie einen effizienten Übergang für die Änderung der Krümmung für niedrige Abschrägungswinkel (im Bezug auf die Fahrzeugdynamik) benötigen.

Formel

Gedämpfte sinusförmige Halbwellen-Tangentenbogen können folgendermaßen ausgedrückt werden:

wobei gilt und x die Entfernung vom Anfangspunkt zu einem beliebigen Punkt des Bogens ist. X wird entlang der Anfangstangente (Tangentenlänge zwischen Tangentenschnittpunkten) gemessen und entspricht dem X-Gesamtwert am Ende des Übergangsbogens.

Andere wichtige Ausdrücke:

Tangentenabstand am Punkt Übergangsbogen-Bogen vom Punkt Tangente-Übergangsbogen:

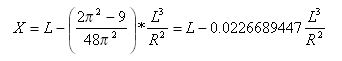
Tangentenversatzabstand am Punkt Übergangsbogen-Bogen zum Punkt Tangente-Übergangsbogen:

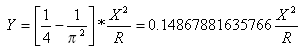
Kubische Parabeln

Kubische Parabeln konvergieren weniger schnell als kubische Parabeln (Japan). Dies führt dazu, dass sie häufig bei der Konstruktion von Bahnstrecken und Straßen eingesetzt werden.

Formel

Mindestradius von kubischen Parabeln

Der Radius beträgt für jeden Punkt einer kubischen Parabel:

Eine kubische Parabel erreicht den Mindestwert für r bei:

Also gilt:

Der Radius einer kubischen Parabel verringert sich von unendlich bis auf bei 24 Grad, 5 Minuten, 41 Sekunden und vergrößert sich von diesem Punkt aus wieder. Aus diesem Grund sind kubische Parabeln für Abschrägungen von mehr als 24 Grad ungeeignet.

Kubische Parabel (Japan)

Dieser Übergang wurde für japanische Anforderungen entwickelt. Die entwickelten Näherungspunkte der Klothoide können in Situationen verwendet werden, in denen Sie einen kleinen Abschrägungswinkel oder einen großen Radius unterbringen müssen. Eine dieser für den Entwurf in Japan verwendeten Näherungen wird Kubische Parabel (Japan) genannt.

Formel

Kubische Parabeln (Japan) können ausgedrückt werden als:

Wobei X = Tangentenabstand am Punkt Übergangsbogen-Bogen zum Punkt Tangente-Übergangsbogen

Diese Formel kann auch ausgedrückt werden als:

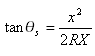
Wobei der zentrale Winkel des Übergangsbogens ist (abgebildet als i1 und i2)

Andere wichtige Ausdrücke:

Tangentenabstand am Punkt Übergangsbogen-Bogen vom Punkt Tangente-Übergangsbogen:

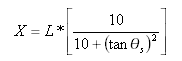
Tangentenversatzabstand am Punkt Übergangsbogen-Bogen zum Punkt Tangente-Übergangsbogen:

NSW Kubische Parabel

Dies ist ein Typ einer modifizierten kubischen Parabel zur Erfüllung der Anforderungen der Normen von New South Wales (Australien).

Formel

NSW Kubische Parabel kann wie folgt ausgedrückt werden:

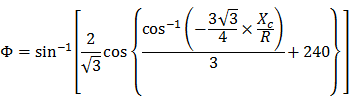
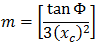
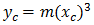
Dabei gilt:

Φ = Winkel zwischen abschließender radialer Linie bei R und senkrechter Linie zur Anfangstangente

R = Radius von Bogen

X_c = Gesamt X des gegebenen Übergangsbogens

Schrammbogen

Schrammbogen verfügen über niedrige Werte in Bezug auf die vertikale Beschleunigung. Sie enthalten zwei Parabeln zweiten Grades, deren Radii als Funktion der Bogenlänge variieren.

Einfache Bogenformel

Krümmung der ersten Parabel:

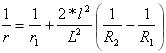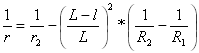für