A continuación se muestran las características de los modos de análisis de estructuras modal, sísmico y sísmico (pseudomodal).
Modo modal
Este enfoque permite el análisis modal de la estructura, que establece los primeros valores n y vectores propios de la estructura.
Los métodos de análisis disponibles son: iteración en el subespacio, método Lanczos y método de reducción de la base.
Las iteraciones se completarán si se cumple la siguiente condición:
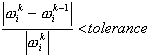
donde i = 1,2,...,n se refiere a los modos de vibración y k es el número de iteraciones.
El límite superior es el valor del periodo (pulsación, frecuencia) que describe que en el rango (0, límite superior) se definirán los siguientes valores y vectores propios.
Es posible realizar una verificación de Sturm, que permite buscar las pulsaciones omitidas.
Modo sísmico
Para los análisis sísmicos y espectrales de la estructura no es esencial que los valores y los vectores propios estén ordenados. Es importante que solo se tengan en cuenta los valores y los vectores propios caracterizados por un elevado coeficiente de participación de masas (que tiene un efecto importante en la respuesta sísmica).
En este modo, se definen los valores n y los vectores propios de la estructura. Los valores definidos no se colocan en orden y es posible que se omitan algunos valores y vectores.
Métodos de análisis disponibles: método Lanczos.
Método de convergencia:

donde:
Φ i : vector propio i-th
Límite superior donde se ignoran los límites.
La verificación de Sturm no se realiza en este modo de análisis de estructuras.
Modo sísmico (pseudomodal)
Este modo se utiliza únicamente para los análisis espectrales y sísmicos. Debe emplearse en los métodos de análisis clásicos basados en los resultados de la descomposición modal con tiempos de análisis de estructura muy largos. Este método consiste en presentar el vector de solución X como una superposición de determinados vectores base que no son la aproximación exacta del modo Φ i .
Métodos de análisis disponibles: método Lanczos.
La verificación de Sturm no se realiza en este modo de análisis de estructuras.
Cuando se selecciona un método de Lanczos en un programa, este cambia el método de cálculo a un método de iteración en el subespacio. Para utilizar el método de Lanczos en los cálculos, las estructuras disyuntas deben estar conectadas de forma que no se modifique el modelo de la estructura (por ejemplo, se debe añadir una barra entre los apoyos).