Uma análise não linear consiste na aplicação incremental de cargas. Durante os cálculos, as cargas não são consideradas em um momento específico, mas são gradualmente aumentadas e soluções para estados de equilíbrio sucessivos são executadas.
O comportamento não linear de uma estrutura pode ser causado por um único elemento de estrutura (não linearidade estrutural ou de material) ou por uma relação de deformação de força não linear em toda a estrutura (não linearidade geométrica).
Os seguintes elementos não lineares podem causar uma não linearidade estrutural:
- Elementos de compressão/tensão
- Elementos de cabo
- Restrições não lineares (ou seja, restrições ou suportes unilaterais, liberações, nós compatíveis com o parâmetro rígido atribuído)
- Plasticidade do material
- Articulações não lineares
Opções de não linearidade geométrica
As opções de não linearidade geométrica levam em consideração os efeitos reais de ordem mais alta e, com frequência, melhoram a convergência do processo de cálculo para uma estrutura, incluindo elementos não lineares.
- Análise P-delta
- Essa análise considera os efeitos de segunda ordem, como alterar a rigidez do elemento sob a influência do estado de tensão no elemento. Também considera a geração de momentos resultantes da ação de forças verticais nos nós deslocados horizontalmente.
- Análise de grandes deslocamentos
- Essa análise considera efeitos de terceira ordem, como a rigidez lateral adicional e tensões resultantes de deformação ou rotação. Esse efeito considera forças adicionais que surgem em uma estrutura deformada, como uma viga com suportes fixos em ambas as extremidades, carregada por uma carga vertical, forças longitudinais que surgem e a deflexão diminui.
Esses parâmetros de análise podem melhorar a convergência do processo de cálculo porque consideram os efeitos reais de ordem mais alta. Isso é especialmente útil ao trabalhar com uma estrutura que inclui elementos não lineares.
É possível usar dois métodos para resolver um sistema de equações não lineares: o método Incremental e o método Comprimento do arco.
Método incremental
Se uma estrutura incluir elementos não lineares (como cabos, suportes unilaterais e plasticidade do material), os cálculos que aplicam o método incremental serão executados.
Com o método incremental, o vetor de carga à direita é dividido em incrementos iguais. Um incremento de carga consecutivo é aplicado à estrutura quando o estado de equilíbrio para o incremento anterior é alcançado. A norma de forças desequilibradas é especificada para cada etapa, permitindo o monitoramento das relações de força-deformação da estrutura.
A figura a seguir mostra um exemplo de um processo não linear usando o processo incremental. Os valores usados para os cálculos não lineares são exibidos.
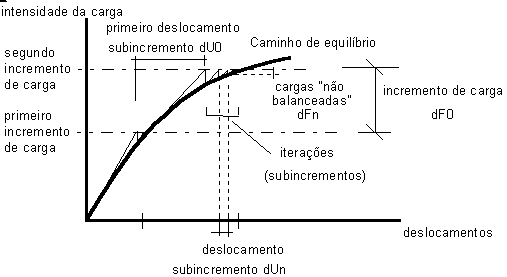
O incremento de carga é usado ao dividir uma carga em segmentos menores. Para estruturas complexas onde o impacto de efeitos não lineares é considerável, é possível que os cálculos não convirjam se a análise para o valor de uma carga for aplicada em uma etapa. O número de incrementos de carga influencia o número de iterações de cálculo. Quanto maior o número de incrementos, maior a probabilidade de os cálculos atingirem o ponto de convergência.
Método de comprimento de arco
O método de comprimento do arco de condução de deslocamento deve ser aplicado quando os algoritmos incrementais de resolução de equações por condução de força não são convergentes.
O método de comprimento de arco é aplicado durante a análise de sobreposição não linear. É altamente recomendado quando os atributos de estrutura não linear são definidos em um modelo de estrutura (consulte o apêndice).
Processo de análise
- O método de tensão inicial.
- O método Newton-Raphson modificado.
- O método completo de Newton-Raphson.
Em geral, o método de tensão inicial é o mais rápido e o método completo de Newton-Raphson é o mais lento. No entanto, a probabilidade de convergência é maior com o método completo de Newton-Raphson do que com o método de tensão inicial.
A tabela a seguir mostra como configurar as opções de atualização da matriz para usar o algoritmo adequado.
| Algoritmo | Atualização da matriz após cada subdivisão | Atualização da matriz após cada iteração |
|---|---|---|
| Tensão inicial | Off | Desativado |
| Newton-Raphson modificado | Ativar | Desativado |
| Newton-Raphson completo | Ativar | Ativar |
O algoritmo do procedimento Broyden-Fletcher-Goldforb-Shanno (BFGS) modifica a matriz de rigidez durante os cálculos. Em alguns casos, o uso do algoritmo de pesquisa de linha pode melhorar a convergência do método.
Quando o estado de equilíbrio é alcançado, o processo de iteração para e a convergência do processo é verificada. Os incrementos de deslocamento Desfazer e as forças desequilibradas Fn são essencialmente zero ou suficientemente pequenos em comparação com os parâmetros de tolerância para ambos os valores. O processo de iteração será interrompido se ocorrer divergência. A falta de convergência pode ser interpretada como o efeito numérico de sobrecargas de estrutura ou como resultado de uma instabilidade de processo numérico, como quando a carga é dividida em um pequeno número de intervalos. Em tais casos, o número de incrementos de carga pode ser aumentado, o que normalmente ajuda o processo a convergir.
Consulte também:
Elementos de barra na análise não linear disponíveis no Robot