In einem linearen Materialmodell muss das Verhältnis zwischen Spannung und Dehnung linear sein, mit einer Steigung E für Elastizitätsmodul (Hookesches Gesetz):

Material-Nichtlinearität ist relevant, wenn die Reaktion bei den Betriebslasten an einem Material über den Teil der Spannungs-/Dehnungskurve hinausgeht, der noch als annähernd linear angesehen werden kann. Viele Materialien haben Kurven, die bei großer Dehnung geringfügig von der Linearität abweichen, sodass ein nichtlineares Materialmodell angesichts all der anderen Unsicherheiten im Modell kaum sinnvoll wäre. Andererseits weichen viele Kurven fast sofort von der Linearität ab, sodass mit einer linearen Annäherung nur sehr grobe Trendstudien durchgeführt werden können.
Die Proportionalitätskonstante bei einem linearen Materialmodell ist das Elastizitätsmodul. Dies ist die Steigung des linearen Teils der Spannungs-/Dehnungskurve (siehe Abbildung unten). Bei sehr nichtlinearen Materialien kann dieses Modul nur bei sehr geringen Dehnungen angewendet werden.
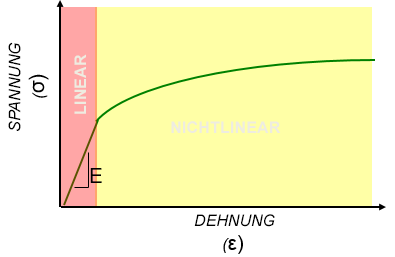
Nichtlineare Materialmodelle für gängige Konstruktionsmaterialien werden definiert, indem man deren Spannungs-/Dehnungskurven angibt. Die meisten Spannungs-/Dehnungskurven repräsentieren nur die Zugreaktion. Wenn ein Material bei Zug und Druck die gleiche Reaktion aufweist, nennt man es symmetrisch. Gusseisen, ist ein gutes Beispiel für asymmetrischen Spannungs-/Dehnungsverhalten, da es bei Druck stärker ist als bei Zug.
Arten von nichtlinearen Materialien
Es gibt verschiedene Arten von nichtlinearem Materialverhalten, das bei einer Strukturanalyse vorkommen kann:
- Nichtlinear elastisch
- Bilinear elastisch-plastisch
- Multilinear plastisch
- Hyperelastisch
- Viskoelastisch
Vereinfachte Modelle der Spannungs-/Dehnungskurven sind nachfolgend dargestellt:
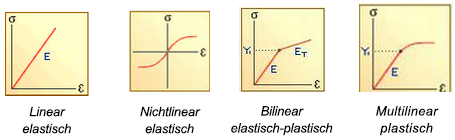
Ein nichtlineares Materialmodell kann als nichtlinear elastisch definiert werden, wenn das Formteil nach Entfernung der Last in den Nullzustand zurückgeht, oder als elastisch-plastisch, wenn sich nach Erreichen der Streckgrenze eine dauerhafte Dehnung aufzubauen beginnt.
Darüber hinaus kann eine elastisch-plastische Spannungs-/Dehnungskurve als bilinear eingegeben werden, wenn nur ein Elastizitätsmodul und ein Plastizitäts- oder Verfestigungsmodul eingegeben werden. Sie kann auch als multilineare Spannungs-Spannungs-Kurve definiert werden, wenn die echte Nichtlinearität des plastische Bereichs mit einer Reihe von Punkten erfasst werden kann.
Inventor Nastran ermöglicht die Definition von zwei weiteren nichtlinearen Materialmodellen: hyperelastisch für Gummi und andere Elastomere und viskoelastisch für zeitabhängige Reaktionen wie Kriechen. Jedes dieser nichtlinearen Materialmodelle erfordert detailliertere Kenntnisse dieser Phänomene, da ihr Verhalten etwas anders ist als bei gewöhnlichen Strukturmaterialien.
Spannungs-/Dehnungskurven
Wie in der folgenden Abbildung zu sehen, sind Nylon, Aluminium und Gusseisen Materialien, bei denen 75 % des Arbeitsbereichs nichtlineare sind. Hier benötigt man ein FEM-Programm wie Inventor Nastran, um die Strukturreaktion auf Betriebslasten zu berechnen.

Spannungs-/Dehnungskurven für Metalle werden in der Regel in Zug- oder Druckprüfungen gemessen. Der Zugtest für Metalle ist ASTM E8. Er gestattet mehrere Dehnungsgeschwindigkeiten und Materialtemperaturen. Die folgenden Diagramme zeigen Spannungs-/Dehnungskurven für Stahl 4340 und Aluminium 2024. Wie Sie sehen, weisen die Stahlkurven zeigen eine einheitliche Steigung bzw. ein einheitliches Elastizitätsmodul bis zur Streckgrenze auf. Die Aluminiumkurve zeigt bei der Untersuchung unterschiedlicher Materialausrichtungen eine Schwankung in der der Spannungs-/Dehnungsreaktion. Die Kurve zeigt auch, dass 2024-T3 asymmetrisch ist, da sich die Zug- und Druckspannungsreaktionen unterscheiden.
Beide Kurven wurden dem Mil Handbook 5H entnommen, das öffentlich zugänglich ist und viele hilfreiche Materialreferenzdaten enthält.

Die untenstehenden Kurven für Noryl, ein PPO von GE Plastics, wurden mit ASTM D638 gemessen, dem Standard-Zugtest für Kunststoffe. Die linke Kurve zeigt, wie sich die Spannungs-/Dehnungsbeziehung bei Kunststoffen mit der Spritzrichtung ändern kann. Die rechte Kurve zeigt, wie dasselbe Material bei unterschiedlichen Dehnungs- oder Belastungswerten und Temperaturen auch unterschiedliche Spannungs-/Dehnungsreaktionen aufweisen kann.

An diesen kurzen Beispielen sehen Sie, wie schnell eine nichtlineare Materialuntersuchung kann sehr komplex werden kann. Daher empfehlen wir Ihnen, die geeignetsten Spannungs-/Dehnungsdaten für das verwendete Material zu besorgen oder darüber nachzudenken, ob die Nichtlinearität des Materials bei den Dehnungsgraden, mit denen Sie arbeiten, überhaupt ein Problem darstellt. Dieser Grad kann mit einer anfänglichen linearen Materialanalyse ermittelt werden. Wenn Sie entscheiden, dass Sie ein nichtlineares Materialmodell benötigen, sollten Sie die Kurve suchen, die Ihre erwartete Umgebung am besten darstellt. Dann bündeln sie die Ergebnisse gegebenenfalls mit 2–3 unterschiedlichen Kurven, um zu sehen, wie empfindlich die relevante Antwort auf diese Nichtlinearität reagiert. Wenn es eine Abweichung gibt und Sie sich nicht entscheiden können, welches Materialmodell besten zutrifft, treffen Sie eine konservative Wahl oder sichern Sie Ihre Analyse mit Testdaten ab.
Bei der Nachbearbeitung der Ergebnisse eines nichtlinearen Materialmodells ist es wichtig, dass Sie verstehen, wie das Material auf Elementbasis versagt. Innerhalb eines jeden Elements gibt es Gaußschen Punkte, an denen die Spannungen bzw. Dehnungen berechnet werden. Für ein nichtlineares Material, sucht Nastran in einer Tabelle nach der Spannungs-/Dehnungskurve für die Spannung an jedem Gaußschen Punkt und meldet dann einen Durchschnitt aller Gaußschen Punkte (d. h. die Mittelspannung) und extrapoliert die Werte der Gaußschen Punkt an den Ecken.
Wenn ein Element einer reinen Axiallast ausgesetzt ist, versagen alle Gaußschen Punkte gleichzeitig, sodass die Spannung in der Mitte genau der eingegebenen Spannungs-/Dehnungskurve entspricht. Bei einer Biegung versagen zuerst die äußeren und dann die inneren Gaußschen Punkte. Dies bedeutet, dass die durchschnittliche Mittelspannung während abrupter Steigungsänderungen auf de Eingabekurve möglicherweise nicht der eingegebenen Spannungs-/Dehnungskurve entspricht. Das liegt daran, dass einige der Gaußschen Punkte an einem Punkt auf der Kurve liegen und die restlichen an einem anderen Punkt. Wenn zwischen der eingegebenen Spannungs-/Dehnungskurve und den ausgegebenen Spannungsergebnissen ein großer Unterschied besteht, ist ein verfeinertes Netz zu empfehlen.
Die beiden folgenden Abbildungen unten zeigen die Spannungs-/Dehnungskurven für zwei unterschiedlichen Netzdichten. Wie Sie sehen, folgt ein feineres Netz genauer der eingegebenen Spannungs-/Dehnungskurve.

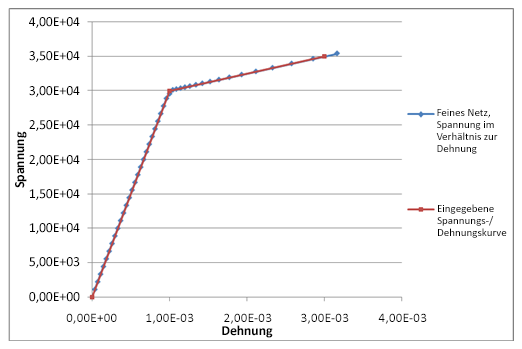
Es ist auch unbedingt zu beachten, dass Spannung an den Ecken anhand der Gaußschen Punkte extrapoliert wird und die Werte daher oft die Spannungswerte der Spannungs-/Dehnungskurve übersteigen können. Wenn zwischen den Spannungswerten in der Mitte und an den Ecken ein großer Unterschied besteht, empfiehlt es sich, das Netz zu verfeinern, um eine genauere Darstellung des auftretenden Versagens zu erhalten.
Anmerkung: NLMATSFACT in Autodesk Inventor Nastran ist eine Stabilisierungsmethode, die bei nichtlinearen Materialanalysen verwendet wird, wenn im Material abrupte Änderungen der Steifheit auftreten. Damit wird gesteuert, wie der Solver während der Iterationen der Spannungs-/Dehnungskurve folgt. Dieser Parameter kann im Dialogfeld Parameter unter "nichtlinear Lösungsparameter eingestellt werden (aktivieren Sie zuerst das Kontrollkästchen "Erweiterte Einstellungen"). Die vorgabemäßige Einstellung AUTO verkleinert automatisch den Skalierfaktor, wenn eine Abweichung auftritt. Bei einem kleinen Wert (z. B. 0,01) ist NLMATSFACT stabiler, erfordert jedoch mehr Iterationen pro Inkrement.
Richtlinien
Die folgenden Richtlinien sollten Sie beim Erstellen eines Modells für eine nichtlineare Finite-Element-Analyse mit nichtlinearen Materialien beachten:
- Beim Ausführen einer Analyse mit großer Dehnung empfiehlt sich die Verwendung eines nichtlinearen elastischen Materials.
- Prüfen Sie, dass die Steigung der Spannungs-/Dehnungskurve (im linearen Bereich) dem Elastizitätsmodul des Materials entspricht.
- Spannungs-/Dehnungsdaten sollten aus einer echten Spannungs-/Dehnungskurve entnommen werden, nicht aus einer technischen Spannungs-/Dehnungskurve. Eine echte Spannungs-/Dehnungskurve berücksichtigt die Verengung oder Verringerung des Querschnittsbereichs während eines normalen Zugspannungstests. Wenn die Steigung der Spannungs-/Dehnungskurve sehr "flach" (oder negativ) ist, erhalten Sie während der Analyse möglicherweise einen nicht positiven definitiven Fehler. Wenn möglich, entfernen Sie den ebenen Bereich der Spannungs-/Dehnungskurve, und führen Sie die Analyse erneut aus. Wenn Sie eine Spannungs-/Dehnungskurve mit flacher oder negativer Steigung verwenden müssen, können Sie versuchen, durch die Einstellung SOLUTIONERROR=AN und FACTDIAG=0 eine Lösung zu erzwingen. Versuchen Sie außerdem, NLMATSFACT auf 0,1-0,5 zu setzen. Diese Parameter können im Dialogfeld „Parameter“ unter „Lösungs-Parameter“ eingestellt werden (aktivieren zuerst das Kontrollkästchen „Erweiterte Einstellungen“).
- Bei Verwendung eines nichtlinearen plastischen Materials ist anstelle der bilinearen Methode eine Spannungs-/Dehnungskurve zu empfehlen. Mit der bilinearen Methode wird eine Spannungs-/Dehnungskurve mit zwei unterschiedlichen Steigungen erstellt. Diese abrupte Änderung des Elastizitätsmoduls erschwert das Konvergieren zu einer Lösung.
|
Vorheriges Thema: Kugelaufprall – Übung |
Nächstes Thema: Biegetestvorrichtung – Übung |