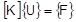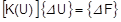Teil 14: Nichtlineare statische Analyse

Es gibt viele Arten von Verhalten, die man als nichtlinear bezeichnen kann. Zu den Beispielen für nichtlineares Verhalten zählen Verschiebungen, die zu einer Änderung der Lastverteilung oder -größe führen, Materialien, die unter Belastung ihre Eigenschaften ändern, oder Lücken, die sich öffnen oder schließen. Das Ausmaß der Nichtlinearität kann gering oder beträchtlich sein.

Linear und nichtlinear im Vergleich

Die Abgrenzung zwischen linear und nichtlinear ist bestenfalls eine Grauzone. Bei der Finite-Elemente-Methode bestimmt üblicherweise ein Satz von Kriterien, ob nichtlineare Effekte für ein bestimmtes Modell wichtig sind. Wenn eines dieser Kriterien zutrifft, ist eine nichtlineare Analyse erforderlich, um reale Verhaltensweisen exakt simulieren zu können. Diese Kriterien gelten zwar immer noch, aber durch neue Möglichkeiten wie z. B. lineare Kontakte und neue Materialien wie Verbundwerkstoffe ist es noch schwieriger geworden, das Erfordernis einer vollständigen linearen Analyse genau abzugrenzen.

Bei einer linearen statischen Analyse gehen wir von folgenden Annahmen aus:

Die meisten Aufgabenstellungen können in der Regel als linear angesehen werden, da die Belastung im linear elastischen Bereich mit geringer Abweichung erfolgt. Bei Aufgabenstellungen dieser Art hat die geringe Nichtlinearität keine Auswirkungen auf die Ergebnisse, und der Unterschied zwischen einer linearen und einer nichtlinearen Lösung ist zu vernachlässigen.

Viele praktische Aufgabenstellungen können zwar durch eine lineare Analyse gelöst werden, aber einige oder alle inhärenten Annahmen treffen möglicherweise nicht zu:

Somit kann ein nichtlinearer Effekt in drei Hauptkategorien eingeteilt werden:

Beachten Sie, dass bei vielen Aufgabenstellungen all diese nichtlinearen Effekte zusammen auftreten können.

Die entsprechenden FEM-Gleichungen lauten wie folgt:

Lineare Analyse

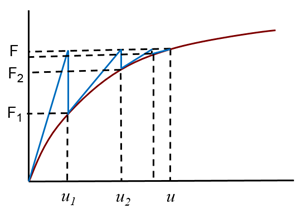
Nichtlineare Analyse

Die Differenz (F – Fi) wird Restkraft genannt.

Der Vorgang wird wiederholt, bis F = Fi ist.

Dabei gilt:

Die globale tangentiale Steifigkeitsmatrix 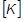ist eine Funktion der globalen Verschiebungen 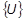, da es sich um eine nichtlineare Aufgabenstellung handelt.

Der aktuelle globale Verschiebungsvektor 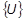ist die Summe der vorhergehenden .

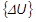Geometrische Nichtlinearität

Die geometrische Nichtlinearität wird relevant, wenn ein oder mehre Bauteile sich verformen, sodass die Annahmen nicht mehr gelten. Die großen Verschiebungseffekte setzen sich aus verschiedenen nichtlinearen Eigenschaften zusammen, beispielsweise:

In den folgenden Abschnitten finden Sie eine Einführung und genauere Beschreibung dieser Eigenschaften.

Große Abweichungen

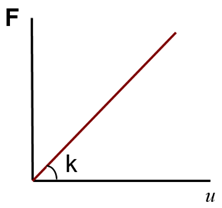
Mit großen Abweichungen sind Bewegungen oder Drehungen eines Bauteils gemeint. Wenn Sie beispielsweise erwarten, dass ein Teil sich um 45 Grad dreht oder abweicht, ist eine nichtlineare Analyse erforderlich. Eigentlich führt jede Drehung um mehr als 10 Grad bei einer linearen Analyse zu einem immer größer werdenden Fehler. Dies liegt daran, dass die lineare Analyse von der Theorie der kleinen Verschiebung ausgeht, bei der sin(θ) ≈ (θ).

Spannungsversteifung

Der Effekt der Spannungsversteifung (manchmal auch geometrische Versteifung genannt) ist am deutlichsten bei dünnen Strukturen, wo die Biegesteifheit im Vergleich zur axialen Steifigkeit sehr klein ist. Stellen Sie sich beispielsweise ein vorversteiftes Fell einer Trommel vor, das einer gleichmäßigen Drucklast ausgesetzt ist. Die Struktur ist rundum am Rand befestigt. Diese dünnwandige Struktur durchläuft eine beträchtliche Spannungsversteifung, während das Teil von der Reaktion auf die Last bei Biegung zur Reaktion auf die Last in der Ebene übergeht.

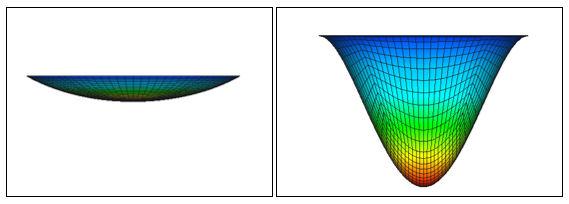
Die folgenden Abbildungen zeigen zwei Ergebnisse des vorversteiften Trommelfells. Die erste Abbildung zeigt eine tatsächliche Abweichung bei Aktivierung von großen Verschiebungseffekten (maximale Abweichung 0,8 Zoll). In der zweiten Abbildung ist die Verformung mit großen Verschiebungen deaktiviert. Beachten Sie, dass die Verformung in der zweiten Abbildung herunterskaliert wurde, da die maximale Abweichung mehr als 5.000 Zoll beträgt.

Ein weiteres Beispiel für Spannungsversteifung ist die Änderung der Tonhöhe einer Gitarrensaite, wenn diese gespannt wird. Das Elastizitätsmodul des Materials der Gitarrensaite ändert sich unter Spannung nicht, aber das System versteift sich dennoch.

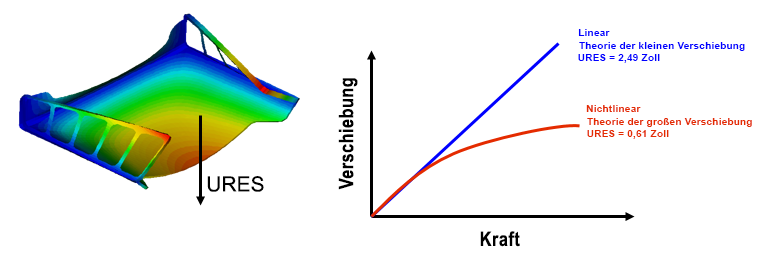
Dünne Platten unter Belastung außerhalb der Ebene mit drei oder vier fixierten Seiten sind ebenfalls häufige Beispiele für Spannungsversteifung. Bei der unten abgebildeten Briefablage prognostiziert ein lineares Modell eine proportionale Reaktion, wenn die verteilte Last auf der Oberfläche des Teils erhöht wird, während das nichtlineare Modell anzeigt, dass die Verschiebung aufgrund des Spannungsversteifungseffekts mit zunehmender Spannung abnimmt.

Anmerkung:

  • Spannungsversteifungseffekte sind auf Zugspannungen zurückzuführen, die aufgrund größerer Verschiebungen entstehen, nicht auf die Verschiebungen selbst. Weder die tatsächliche Verschiebung im Modell noch die Größe der Zugspannung ist ein klarer Hinweis auf den Grad der Nichtlinearität. Eine ähnliche Spannung bei einer Geometrie oder Lastrichtung kann zu erheblich geringerer Spannungsversteifung führen als bei einer anderen.
  • Die beste Möglichkeit, um zu ermitteln, ob große Verschiebungseffekte auftreten, ist ein Vergleich mit den Ergebnissen kleiner Verschiebungen. Führen Sie die Aufgabenstellung also zuerst als lineare Analyse und anschließend als nichtlineare Analyse unter Berücksichtigung von Spannungsversteifung oder großen Verschiebungseffekten durch.
  • Oft können vereinfachte Modelle verwendet werden, um die Bedeutung der Verschiebungseffekte zu bestimmen.
  • Wenn sich die Ergebnisse kleiner und großer Verschiebungen NUR hinsichtlich der Größe unterscheiden, sind die Trends aus dem Einsatz von Methoden für kleine Verschiebungen gültig.

Brechen und Knicken

Zu anderen häufigen geometrisch nichtlinearen Situationen gehören Bruch- und Knickprobleme, häufig auch bistabile oder multistabile Systeme genannt. Bei vielen Bruchproblemen ist das Verhalten nahezu linear bis zu dem Punkt, an dem eine kleine zusätzliche Last eine große Abweichung erzeugt, wenn eine sekundäre stabile Position erreicht ist. Die Erfassung dieses Bruch- oder Bifurkationspunkts ist eine sehr schwierige numerische Aufgabe. Sobald ein Benutzer festgestellt hat, dass ein Problem mit Bruch oder Knickung vorliegt, kann der Konstrukteur das Wissen, dass die FEM-Solver beim Versuch der Modellierung des Bruchs möglicherweise versagen, zu seinem Vorteil nutzen. Anhand des Solverversagens selbst kann er bestimmen, bei welcher Last eine Knickung wahrscheinlich auftritt.

Starke Dehnung

Der Effekt einer starken Dehnung ist fast immer mit einem nichtlinearen Materialmodell verbunden, da dies eine plastische Bruttoverformung beinhaltet. Kaltstauchung, das Zusammendrücken von Gummidichtungen und Metallumformung sind gute Beispiele für eine starke Dehnungsreaktion.

Material-Nichtlinearität

Zwischen der linearen und nichtlinearen Materialreaktion kann ein erheblicher Unterschied bestehen. Weitere Informationen hierzu finden Sie unter dem Thema Nichtlineare Materialien. Bei jedem Material außer Stahl versteht man die Nichtlinearität der Aufgabenstellung am besten, indem man die Spannungs-/Dehnungskurven prüft. (Auch wenn Sie mit einem linearen Materialmodell arbeiten, ist es für die Interpretation der Ergebnisse wichtig, die Nichtlinearität zu kennen.)

Vereinfachte Modelle der Spannungs-/Dehnungskurven sind nachfolgend dargestellt:

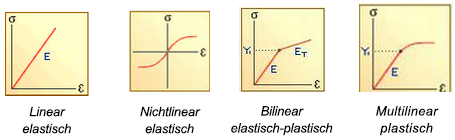
Ein lineares Modell kann fundierte Daten für viele Materialien liefern:

Eine lineare Analyse kann lediglich den Beginn des Versagens prognostizieren. Wenn die Grenzwerte überschritten werden, nimmt die Korrelation mit der Komplexität des Spannungszustands ab.

Eine nichtlineare Plastizitätsanalyse kann lediglich den Beginn einer Fraktur prognostizieren. Die nichtlinearen Materialeffekte können wichtig sein, wenn Sie wissen möchten, was nach dem anfänglichen Materialversagen geschieht.

Alternativ können nichtmetallische Materialien wie Gummi und Kunststoff auch bei geringen Dehnungswerten eine sehr nichtlineare Spannungs-/Dehnungskurve aufweisen. Daher ist ein genaues Bild der Materialsteifheit über den gesamten Dehnungsbereich hinweg wichtig für eine genaue Prognose der Steifigkeit des gesamten Modells.

Bei spröden Materialien wie z. B. Gusseisen treten vor dem Versagen geringe unelastische Verformungen auf. Daher stellt eine lineare Analyse bei dieser Art von Materialien in der Regel kein Problem dar.

Die meisten Materialien und sogar Metalle haben jedoch ein gewisses Maß an Duktilität. Aufgrund dieser Duktilität können Hotspots lokal versagen, wodurch sich die Spannungen im Vergleich zur Prognose einer linearen Analyse verringern.

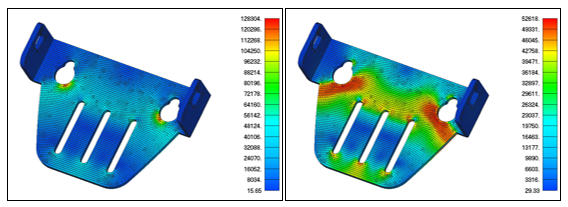
Die Metallhalterung aus der folgende Abbildung zeigt die höchst unterschiedliche Spannungsverteilung zwischen linearen und nichtlinearen Materialien. Das Metall hat eine Streckgrenze von 50 ksi. Das linke Bild enthält die Ergebnisse einer linearen Materialanalyse und zeigt Spitzenspannungen deutlich über der Streckgrenze. Die nichtlineare Materialanalyse auf der rechten Seite weist aufgrund der Spannungsumverteilung eine ganz andere Kontur auf. Bei der nichtlinearen Materialanalyse lag die größte plastische Dehnung bei 1 %.

Randbedingungs-Nichtlinearität

Ein Modell weist eine Randbedingungs-Nichtlinearität auf, wenn die Lasten, Abhängigkeiten oder Lastpfade sich während der Lösung ändern. Wenn die Ausrichtung, Verteilung oder Größe der angewendeten Lasten bzw. des Lastpfads sich mit zunehmender Belastung erhöht, ist möglicherweise ein nichtlineares Modell erforderlich. Die häufigsten Randbedingungs-Nichtlinearitäten sind:

In den folgenden Abschnitten finden Sie eine Einführung und genauere Beschreibung dieser Eigenschaften.

Kontakt

Kontaktbedingungen modellieren die Interaktion zweier separater Bauteile oder unterschiedlicher Flächen eines Bauteils. Randbedingungen wie Flächenkontakt werden im Allgemeinen als nichtlinear angesehen. In letzter Zeit hat sich jedoch ein Trend entwickelt, der bei einigen FEM-Anwendungen die Ausführung einer Kontaktanalyse in einer linearen Lösung erlaubt. Bei der Entscheidung zwischen linearer und nichtlinearer Kontaktanalyse stellt man sich am besten diese Fragen:

  • Gibt es im Modell große Bewegungen oder nichtlineare Effekte, wie oben erwähnt?
  • Gibt es im Modell ein beträchtliches Gleiten zwischen Körpern? Ist die Kontaktlösung pfadabhängig (z. B. bei einem Schnappverschluss)?
  • Werden im Modell detaillierte Kontaktspannungen benötigt?

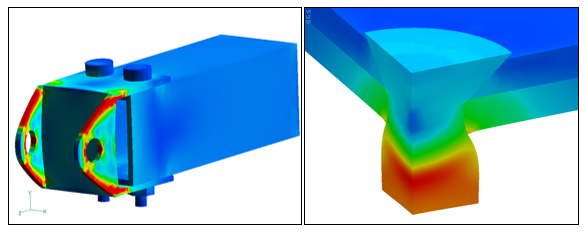
Wenn die Antwort auf eine dieser drei Fragen ja lautet, ist in der Regel die Durchführung einer nichtlinearen Lösung zu empfehlen, um das bestmögliche Ergebnis zu erzielen. Die beiden folgenden Modelle zeigen zwei Beispiele zur Verwendung von linearen und nichtlinearen Lösungen. Das Modell der Anhängerkupplung auf der linken Abbildung besteht zwar aus sechs Teilen in einer Baugruppe, kann aber als lineare Kontaktlösung ausgeführt werden, da sich zunächst alle Bauteile berühren und die Verschiebungen klein sind. Das Nietenmodell auf der rechten Seite hingegen erfordert wegen der großen Verschiebungen und der Notwendigkeit eines nichtlinearen plastischen Materialmodells eine nichtlineare Lösung.

Weitere Informationen zur Kontaktmodellierung finden Sie im Benutzerhandbuch unter dem Thema Oberflächenkontakte

Nachlaufende Kräfte

Dieser nichtlineare Effekt bedeutet einfach, dass sich die Richtung der Kräfte mit den Verformungen bzw. der Bewegung des Bauteils ändert. Drucklasten sind ein perfektes Beispiel für nachlaufende Kräfte, da sie immer lotrecht zur Fläche wirken. Wenn ein Bauteil sich verformt, passen die nachlaufenden Kräfte die Richtung der Lasten an, um sicherzustellen, dass sie weiterhin lotrecht zur Fläche sind.

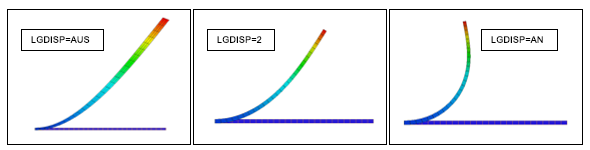
Der unten abgebildete Auslegerbalken hat an der Spitze eine Drucklast von 100 psi. Es werden drei Analysen mit unterschiedlich großen Verschiebungen durchgeführt (unter Verwendung des Parameters LGDISP in Inventor Nastran).

Die Ergebnisse der drei Durchläufe sind unten abgebildet. Das erste Bild zeigt das unrealistische "Wachstum", das auftritt, wenn große Verschiebungseffekte deaktiviert sind (LGDISP=AUS). Das zweite Bild zeigt die Ergebnisse, wenn große Verschiebungen aktiviert, aber nachlaufende Kräfte deaktiviert sind (LGDISP=2). Beim letzten Bild sind sowohl große Verschiebungen als auch nachlaufende Kräfte aktiviert (LGDISP=AN). Dies bietet die größte Genauigkeit.

Weitere Informationen zum Einrichten einer nichtlinearen Analyse in Autodesk Inventor Nastran finden Sie im Benutzerhandbuch unter den Themen Nichtlinear und Nichtlineare Optionen.

Nichtlinearer Elementtyp

Das nichtlineare Element Kabel mit reiner Zugspannung steht in Inventor Nastran zur Verfügung.

Das Element "Kabel mit reiner Zugspannung" ist in Inventor Nastran als Verbinder definiert. Klicken Sie in der Strukturansicht mit der rechten Maustaste auf Verbinder und wählen Sie Bearbeiten. Wählen anschließend den Typ Kabel (weitere Informationen finden Sie im Benutzerhandbuch unter dem Thema Kabelverbindung). Ein Material muss gemeinsam mit einer Querschnittsfläche referenziert werden. Sie können entweder eine anfängliche Spannung oder ein ursprünglicher Kabelspielraum angeben. Bei der anfänglichen Spannung kann der Typ des Vorspannmoments im gleichen Dialogfeld auf anfänglich eingestellt werden. Mit dieser Einstellung wird die anfängliche Spannung anfängliches Vorspannmoment behandelt. Dieser Wert wird durchgehend zur internen Axialbelastung des Elements hinzugefügt, die durch die Verschiebung der Endknoten erzeugt wird. Durch die Typeinstellung Durchgehend muss die anfängliche interne Last des Kabels unabhängig von den Knotenverschiebungen immer die anfängliche Zugspannung sein. Die Verwendung der Einstellung "Durchgehend" führt möglicherweise dazu, dass die Konvergenz bei nichtlinearen Iterationen langsamer verläuft als gewöhnlich.

Das Kabelelement muss über eine Referenz auf ein lineares isotropes Material verfügen, kann jedoch temperaturabhängig sein. Es werden sowohl thermische als auch träge Elementlasten unterstützt. Wenn das Kabelelement seitlicher Belastung ausgesetzt sind, benötigt es etwas Biegungssteifigkeit. Die vorgegebene Biegungssteifigkeit basiert auf dem Quadrat der Fläche eines runden Querschnitts.

Allgemeine Richtlinien

Die folgenden Richtlinien sollten Sie beim Erstellen eines Modells zur nichtlinearen Finite-Elemente-Analyse beachten:

  1. Führen Sie die Analyse zuerst als lineare statische Lösung durch und gehen Sie sicher, dass die Ergebnisse Ihren Erwartungen entsprechen.
  2. Halten Sie die Modellgröße klein. Vereinfachen Sie die Geometrie vor der Netzgenerierung so weit wie möglich (unnötige Abrundungen, Bohrungen usw. sollten entfernt werden). Ermitteln Sie Symmetriebereiche, schneiden Sie das Modell an diesen Ebenen und wenden Sie Symmetrierandbedingungen an. Mit Symmetrie wird nicht nur die Modellgröße erheblich reduziert. Die symmetrischen Abhängigkeiten stabilisieren das Modell auch gegen die Bewegungen starrer Bauteile.
  3. Sorgen Sie für ein hochwertiges Netz. Die Konvergenz einer nichtlinearen Analyse kann durch Elemente minderer Qualität beeinträchtigt werden. Bei einer einfachen Geometrie sollten Sie für Festkörperelemente ein Plattennetz oder ein Hex-Netz in Betracht ziehen. Führen Sie Verzerrungsprüfungen durch, um sicherzustellen, dass es keine stark verzerrte Elemente gibt.
  4. Wenden Sie nichtlineare Materialien nur in Modellbereichen an, in denen Sie nichtlineares oder plastisches Verhalten erwarten. Dies trägt zur Beschleunigung der Analyse bei und kann die Konvergenzrate steigern.

Wenn der Oberflächenkontakt verwendet wird, teilen Sie die Kontaktflächen dort in bestimmte Bereiche auf, wo Sie in Kontakt erwarten. Durch die Verwendung umfassender oder allgemeiner Flächen wird eine große Anzahl von Kontaktelementen generiert, die Analysedauer verlängert.

Fehlerbehebung

Für die Fehlerdiagnose bei der Durchführung einer nichtlinearen statischen Analyse sollten Sie in folgenden Schritten vorgehen:

  1. Führen Sie das Modell in einer linearen statischen Lösung aus. Stellen Sie sicher, dass die Ausführung normal abgeschlossen wurde und die Ergebnisse richtig aussehen. Prüfen Sie außerdem, ob der Epsilonwert ist klein ist (< 1,0E-7) und lesen Sie eventuelle Warnmeldungen.
  2. Richten Sie eine nichtlineare Analyse ein, bei der große Verschiebungseffekte deaktiviert sind. Ändern Sie LGDISP=AUS im Dialogfeld Parameter im Bereich Nichtlineare Lösungsparameter. Weitere Informationen hierzu finden Sie im Benutzerhandbuch unter dem Thema Parameter. Wenn in der Modelleingabedatei PARAM,LGDISP,1 oder AN angezeigt wird, ändern Sie dies in AUS.
  3. Deaktivieren Sie alle nichtlinearen Materialien, indem Sie die Karte MATS1 im Nastran-Deck auskommentieren. Weitere Informationen zum Vornehmen von Änderungen an der Nastran-Massendatendatei finden Sie im Benutzerhandbuch unter dem Thema Nastran-Datei generieren.
  4. Wenn das Modell nach den Schritten 2 und 3 immer noch nicht ausgeführt wird, gehen Sie in die Einstellungen der nichtlinearen Analyse, setzen Sie die Anzahl der Inkremente auf 1, die Ausgabesteuerung auf JA und die maximalen Halbierungen (unter der Schaltfläche "Erweitert") auf 1. Damit sollten Sie einen Ausgabesatz mit Ergebnissen erhalten, die Sie für die Diagnose der Probleme in Ihrem Modell untersuchen können.
  5. Wenn es Ihnen gelingt, das Modell wie unter Schritt 2 beschrieben auszuführen, aktivieren Sie große Verschiebungseffekte und prüfen Sie, ob das Modell weiterhin konvergiert. Wenn dies der Fall ist, aktivieren Sie das nichtlineare Material und prüfen Sie, ob das Modell konvergiert.
  6. Wenn das Modell nach Aktivierung des nichtlinearen Materials nicht mehr konvergiert, finden Sie weiterführende Informationen unter dem Thema Nichtlineare Materialien.

Wenn Sie die Fehlermeldung E5001: NICHT POSITIVES DEFINITES ELEMENT AN RASTER id KOMPONENTE n IDENTIFIZIERTerhalten, empfehlen wir Ihnen, bei der Ermittlung der Fehlerursache in folgenden Schritten vorzugehen:

  1. Führen Sie das Modell in einer linearen statischen Lösung aus und stellen Sie sicher, dass sie abgeschlossen wird und die Ergebnisse richtig erscheinen.
  2. Wenn die lineare statische Analyse funktioniert, führen Sie das Modell als nichtlineare Analyse aus und verwenden Sie den VIS-Solver. Der VIS-Solver wird im Dialogfeld "Parameter" unter "Kontrollanweisungen – DECOMPMETHOD" ausgewählt (siehe Thema Parameter im Benutzerhandbuch.) Ändern Sie außerdem MAXSPARSEITER in 500 Iterationen, um die Analysezeit zu verkürzen. Das Ziel ist eine Lösung zur Fehlerdiagnose zu erzwingen. Im Gegensatz zu allen Solvern erzeugt der VIS bei einer falsch konfigurierten Steifigkeitsmatrixerstellt keinen schwerwiegenden Fehler.
  3. Ändern Sie im Nastran-Deck auf der NLPARM-Karte die Anzahl der Iterationen auf 1 (Feld 3) und die maximale Anzahl der Iterationen 1 (Feld 7).
  4. Führen Sie diese Analyse aus und sehen Sie sich die Ergebnisse an. Bedenken Sie, dass dies lediglich ein Diagnosedurchlauf ist und die Ergebnisse nicht als echte Ergebnisse behandelt werden sollten. Wenn Sie einen Bereich oder einen Knoten mit großer Verschiebung/Spannung sehen, ist dies wahrscheinlich die Ursache des schwerwiegenden Fehlers. Dies durch kann stark verzerrte Elemente verursacht werden.

Vorheriges Thema: Iterationen vergleichen – Übung

Nächstes Thema: Flachwandiger Behälter – Übung

Themen in diesem Abschnitt