Existen varios tipos de solucionadores iterativos.
ICCF iterativo
Este método se recomienda para problemas de gran escala con un número reducido de lados a la derecha.
- Uso de memoria: alto.
- Uso del disco: no se utiliza.
- Estimación de velocidad: rápida (para problemas bien acondicionados).
- Cantidad de ecuaciones: 15 000 - 1 000 000 ecuaciones y más.
- Análisis admitidos: estática lineal, análisis modal, pandeo.
- Limitaciones de análisis disponibles: N/D.
- Otras limitaciones:
- La corrección de las restricciones de la estructura no está activada.
- La convergencia es lenta si algunos problemas se han condicionado de forma incorrecta.
Diagonal iterativa
Este método se recomienda para problemas de gran escala con un número reducido de lados a la derecha.
- Uso de memoria: mínimo
- Uso del disco: mínimo
- Estimación de velocidad: lenta
- Cantidad de ecuaciones: 15 000 - 1 000 000 ecuaciones y más.
- Análisis admitidos: estática lineal, análisis modal, pandeo.
- Limitaciones de análisis disponibles: N/D
- Otras limitaciones:
- La corrección de las restricciones de la estructura no está activada.
- La convergencia es lenta si algunos problemas se han condicionado de forma incorrecta.
Gauss-Cholesky iterativo
Este método se recomienda para problemas de gran escala con un número reducido de lados a la derecha, cuando no hay suficiente RAM para utilizar el método ICCF.
La verificación de cada matriz de elementos se realiza mediante el procedimiento de regularización de Vinget 12.
- Uso de memoria: mínimo
- Uso del disco: mínimo
- Estimación de velocidad: lenta
- Cantidad de ecuaciones: 15 000 - 1 000 000 ecuaciones y más.
- Análisis admitidos: estática lineal, análisis modal, pandeo.
- Limitaciones de análisis disponibles: N/D
- Otras limitaciones:
- La corrección de las restricciones de la estructura no está activada.
- La convergencia es lenta si algunos problemas se han condicionado de forma incorrecta.
ICCF iterativo multinivel
Este método se recomienda para problemas de gran escala con un número reducido de lados a la derecha. Muestra una convergencia más rápida que el método ICCF iterativo.
- Uso de memoria: alto
- Uso del disco: mínimo
- Estimación de velocidad: rápida para problemas bien acondicionados
- Cantidad de ecuaciones: 15 000 - 1 000 000 ecuaciones y más.
- Análisis admitidos: estática lineal, análisis modal, pandeo.
- Limitaciones de análisis disponibles: tipos de estructura disponibles: 3D (barra, lámina, sólido y todos los elementos finitos especiales), pórtico 2D.
- Otras limitaciones:
- La corrección de las restricciones de la estructura no está activada.
- Convergencia menos estable, en algunos casos.
Diagonal multinivel iterativa
Este método es considerablemente más lento que el ICCF iterativo multinivel. Sin embargo, requiere mucho menos memoria RAM.
El método de alisamiento 2 suele requerir menos iteraciones en comparación con el método ICCF iterativo multinivel.
La verificación de cada matriz de elementos se realiza mediante el procedimiento de regularización de Vinget 1,2.
- Uso de memoria: mínimo
- Uso del disco: mínimo
- Estimación de velocidad: lenta
- Cantidad de ecuaciones: 15 000 - 1 000 000 ecuaciones y más.
- Análisis admitidos: estática lineal, análisis modal, pandeo.
- Limitaciones de análisis disponibles: tipos de estructura disponibles: 3D (barra, lámina, sólido y todos los elementos finitos especiales), pórtico 2D.
- Otras limitaciones:
- La corrección de las restricciones de la estructura no está activada.
Gauss-Cholesky iterativo multinivel
Este método es considerablemente más lento que el ICCF iterativo multinivel. Sin embargo, requiere mucho menos memoria RAM.
El método de alisamiento 2 suele requerir menos iteraciones en comparación con el método ICCF iterativo multinivel.
La verificación de cada matriz de elementos se realiza mediante el procedimiento de regularización de Vinget 1,2.
- Uso de memoria: mínimo
- Uso del disco: mínimo
- Estimación de velocidad: media (para problemas bien acondicionados)
- Cantidad de ecuaciones: 15 000 - 1 000 000 ecuaciones y más.
- Análisis admitidos: estática lineal, análisis modal, pandeo.
- Limitaciones de análisis disponibles: tipos de estructura disponibles: 3D (barra, lámina, sólido y todos los elementos finitos especiales), pórtico 2D.
- Otras limitaciones:
- La corrección de las restricciones de la estructura no está activada.
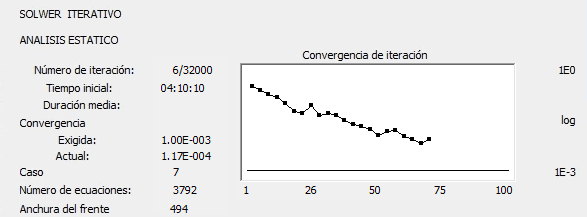
Cálculos de métodos iterativos
El cuadro de diálogo de cálculos del método iterativo muestra el proceso de convergencia del método iterativo si se alcanza el nivel de precisión definido por el usuario o si el proceso es divergente.
- Número de iteraciones actual / número máximo de iteraciones.
- Precisión requerida.
- Precisión de la iteración actual.
- Número de ecuaciones.
- Anchura del frente.