Es recomendable usar el método de iteración en el subespacio por bloques para el cálculo de estructuras de gran tamaño con una cantidad excesiva de modos que se calcularán.
Los métodos de iteración en el subespacio resuelven el sistema de ecuaciones de problemas de valores propios Kφ - λBφ = 0.
Este método suele ser más rápido que el de Lanczos.
La tolerancia (convergencia requerida) de la solución del problema propio se determina mediante la siguiente fórmula:
![]()
El parámetro de tolerancia (tol) se define en el cuadro de diálogo Parámetros del análisis modal. La precisión de los cálculos se puede aumentar mediante la reducción del valor tol de tolerancia. Esto da como resultado el crecimiento del número de iteraciones.
Cálculos
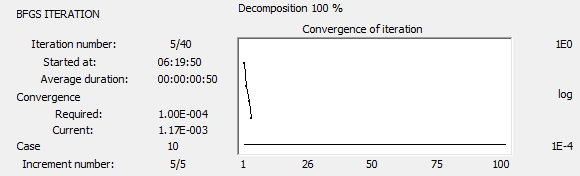
El cuadro de diálogo de cálculos del método de iteración en el subespacio presenta las siguientes fases:
- Número de iteraciones actual / número máximo de iteraciones
- Precisión requerida (tolerancia)
- Precisión de la iteración actual
- Número de modos necesarios
Consulte también lo siguiente: