Uogólniony problem wartości własnej ma następującą postać:
K φ — λM φ = 0,
gdzie K, M oznaczają odpowiednio macierze sztywności i mas, {φ, λ} — pary własne (postać drgań własnych i wartość własna).
Definiowane są dwa typy wektorów rezydualnych:

gdzie {φ, λ} są obliczonymi parami własnymi, w których występują pewne błędy obliczeniowe. Pierwsze wyrażenie definiuje wektor rezydualny dla sił, a drugie dla przemieszczeń.
Stosowane są trzy różne kryteria szacowania błędów obliczeniowych dla wektorów własnych:

Metody
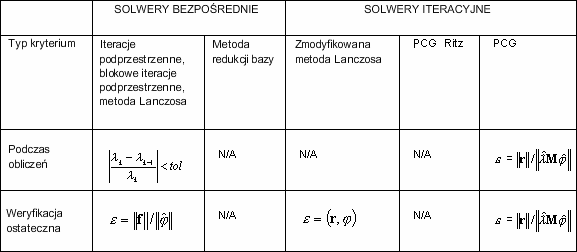
Komentarze
- Precyzja w trakcie trwania obliczeń konstrukcji dla metody Lanczosa i zmodyfikowanej metody Lanczosa (solwer iteracyjny) w trybie pseudosejsmicznym nie jest wyznaczana. Przeprowadzana jest jedynie weryfikacja ostateczna.
- Przeprowadzana jest kontrola zbieżności
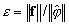 na każdym z 20 kroków Lanczosa w metodzie Lanczosa dla trybu sejsmicznego. Parametr tol znajdujący się w oknie dialogowym Parametry Analizy Modalnej jest pomijany.
na każdym z 20 kroków Lanczosa w metodzie Lanczosa dla trybu sejsmicznego. Parametr tol znajdujący się w oknie dialogowym Parametry Analizy Modalnej jest pomijany. - Metoda redukcji bazy i metoda PCG_Ritz są metodami Ritza. Ponieważ nie jest to podejście iteracyjne, nie jest przeprowadzana weryfikacja precyzji. Parametr tol znajdujący się w oknie dialogowym Parametry Analizy Modalnej jest pomijany.
- Metoda PCG dla solwera iteracyjnego stosuje najsztywniejsze kryteria zbieżności
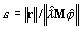 w trakcie procesu obliczeniowego. Parametr tol znajdujący się w oknie dialogowym Parametry Analizy Modalnej – Solwer Iteracyjny definiuje górną granicę dla ε, tak więc ε ≤ tol jest warunkiem zatrzymania iteracji.
w trakcie procesu obliczeniowego. Parametr tol znajdujący się w oknie dialogowym Parametry Analizy Modalnej – Solwer Iteracyjny definiuje górną granicę dla ε, tak więc ε ≤ tol jest warunkiem zatrzymania iteracji.
Nie należy mylić precyzji z tolerancją określoną w oknie dialogowym Parametry Analizy Modalnej podczas stosowania solwerów bezpośrednich (skyline lub sparse), gdy wybrany jest tryb modalny. Tolerancja podczas obliczeń definiowana jest według następującego wzoru:
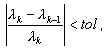
gdzie λk, λk—1 — dwie kolejne wartości własne na k—tym i k—1 kroku iteracji, a tol oznacza tolerancję, przyjmowaną w oknie dialogowym Parametry analizy modalnej. Określenie ostatecznej dokładności obliczeń (1—3) jest procedurą czasochłonną i jest dokonywane w końcowej fazie analizy modalnej jako weryfikacja otrzymanej precyzji. Zwiększenie dokładności obliczeń jest możliwe poprzez zmniejszenie wartości tolerancji tol; powoduje to wzrost liczby iteracji.
Jeżeli precyzja niektórych postaci po obliczeniach nie jest wystarczająca, to konieczne jest.
|
Solwery bezpośrednie |
SOLWERY ITERACYJNE |
|||
|---|---|---|---|---|
|
Iteracje podprzestrzenne, blokowe iteracje podprzestrzenne, Metoda Lanczosa |
Metoda redukcji bazy |
Zmodyfikowany algorytm Lanczosa |
PCG_Ritz |
PCG |
|
Zmniejszenie wartości tol w oknie dialogowym Parametry analizy modalnej |
Zwiększenie liczby węzłów bazowych i kierunków bazowych |
Zmniejszenie wartości tol w oknie dialogowym Parametry solwera iteracyjnego i zwiększenie liczby postaci |
Zwiększenie liczby postaci |
Zmniejszenie wartości tol w oknie dialogowym Parametry analizy modalnej |
Patrz również: