Całkowanie równań ruchu to analiza pozwalająca sprawdzić reakcję konstrukcji w wybranych punktach czasowych na zadane wymuszenie w czasie (w przeciwieństwie do innych typów analiz dostępnych w programie Robot, które dają odpowiedź w formie amplitud wyłącznie w jednej, ustalonej chwili).
Całkowanie równań ruchu polega na uzyskaniu rozwiązania następującego równania zmiennej czasowej „t”:
M * a(t) + C * v(t) + K * d(t) = F(t)
ze znanymi wartościami początkowymi d(0)=d0 i v(0)=v0,
gdzie:
M — macierz mas
K — macierz sztywności
C = a * M + b * K — macierz tłumienia
α — mnożnik podawany przez użytkownika
β — mnożnik podawany przez użytkownika
d — wektor przemieszczeń
v — wektor prędkości
a — wektor przyspieszeń
F — wektor obciążeń.
Wszystkie wyrażenia z parametrem (t) są zależne od czasu.
Przy rozwiązywaniu postawionego powyżej zadania używana jest metoda Newmarka lub metoda dekompozycji. Metoda Newmarka należy do grupy algorytmów, które są bezwarunkowo zbieżne przy odpowiednio dobranych parametrach metody. Metoda stosuje następujące wzory na wartości przemieszczeń i prędkości w następnym kroku całkowania:
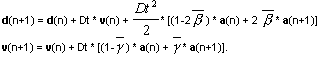
Parametry β i γ sterują zbieżnością i dokładnością wyników otrzymanych przy pomocy tej metody.
Bezwarunkowa zbieżność jest zapewniona dla 0,5 ≤ γ ≤ 2 * b.
W programie przyjmowane są następujące wartości parametrów: b = 0.25 i g = 0.5. Możliwa jest zmiana tych wartości, ale jedynie w przypadku wykorzystywania liniowej analizy całkowania równań ruchu, gdy wybrana jest metoda Newmarka lub Newmarka (przyspieszeniowa). Modyfikacja tych wartości (parametry TransBeta i TransGamma) jest możliwa w pliku preferencyjnym *.COV zapisanym w katalogu CFGUSR; aby obliczenia były przeprowadzone dla innych wartości parametrów b i g, parametry TransBeta i TransGamma należy zmieniać w pliku *.COV, a następnie wczytać ten plik preferencyjny do programu Robot.
Metoda Newmarka jest zalecana w przypadku krótkich historii czasowych, kiedy konstrukcja poddawana jest obciążeniom skupionym. Takie obciążenia spowodują ruch, który będzie wymagał dużej liczby form własnych do jego opisu. Stąd też dla tego typu zadań metoda Newmarka będzie bardziej efektywna niż metoda dekompozycji modalnej. Metoda Newmarka wykorzystuje wyjściowe równania ruchu bez żadnych uproszczeń. Dokładność uzyskanych wyników zależy od dokładności integracji numerycznej równań czasu i jest definiowana przez wartość z przedziału czasowego dla wybranych parametrów α, β. Metoda nie wymaga rozwiązania problemu własnego do uzyskania wartości i wektorów własnych. Dla długich historii czasowych metoda jest jednak czasochłonna, gdyż należy prowadzić obliczenia dla dużej liczby przedziałów czasowych z wymaganą dokładnością.
Metoda Hilber-Hughes-Taylor (HHT) pozwala na wprowadzenie numerycznego tłumienia wyższych częstości bez utraty dokładności rozwiązania. Dyskretna forma równania ruchu ma następującą postać:
gdzie:
—1/3 ≤ α ≤ 0
Przyjmując:
uzyskujemy bezwarunkowo stabilny schemat całkowania z dokładnością drugiego rzędu.
Dla postaci przyspieszeniowej wielkości ‘próbne’ w n+1 kroku całkowania wyznaczamy
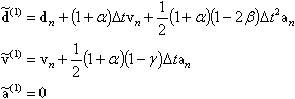
Metoda HHT jest bardzo efektywnym algorytmem całkowania numerycznego pozwalającym na usunięcie niekorzystnego wpływu wysokich częstotliwości na jakość rozwiązania.
Prostą metodą otrzymania wymaganego rozwiązania jest zastosowanie metody dekompozycji modalnej, która oparta jest na reprezentacji ruchu konstrukcji jako superpozycji ruchu dla niesprzężonych form. Dlatego też metoda ta wymaga określenia wartości własnych i wektorów własnych. Do tego celu polecamy wykorzystanie metody Lanczosa. Powinna być również wykonana weryfikacja Sturma. Metoda dekompozycji modalnej stosuje zredukowane niesprzężone równania.
Równanie ruchu (bez tłumienia) można zapisać w postaci:
gdzie
,
Ng — liczba „grup obciążenia”, φk(t) — równanie ruchu a dla k-tej grupy obciążeń.
(2)
Dzięki wstawieniu równania (2) do równania (1) oraz uwzględnieniu tłumienia modalnego i warunków ortogonalności 
, otrzymujemy poniższe równanie.
gdzie 
, ξ — parametry tłumienia modalnego, ωi — częstotliwość dla i-tej formy.
Każde z równań ruchu jest rozwiązywane numerycznie z dokładnością drugiego rzędu. Końcowy wektor przemieszczenia X(t) dla zdefiniowanych punktów czasowych t* = t1, t2, … otrzymuje się po wstawieniu qi(t*), i=1,2,…,m do równań (2).
Warto zwrócić uwagę na różnice między opisywanymi w tym rozdziale typami analiz, które użytkownik ma do dyspozycji w programie. Analiza obciążeń ruchomych różni się od Całkowania Równań Ruchu tym, że nie uwzględnia efektów dynamicznych. Różnica pomiędzy analizą harmoniczną a Całkowaniem Równań Ruchu polega na tym, że pierwszy typ analizy wyznacza odpowiedź konstrukcji wyłącznie w formie amplitud, a nie jako funkcje czasu.
Patrz również: