Definice přechodnic

Ve vztahu k dalším tečnám nebo obloukům je každá přechodnice buď vnitřní oblouk, nebo vnější oblouk.

Dvěma nejběžnějšími parametry, které se používají při návrhu a nastavení přechodnice, jsou L (délka přechodnice) a R. Parametr R označuje poloměr zakřivení na jednom konci přechodnice. K rozlišení poloměru na začátku a na konci přechodnice lze použít hodnoty R₁ a R₂.

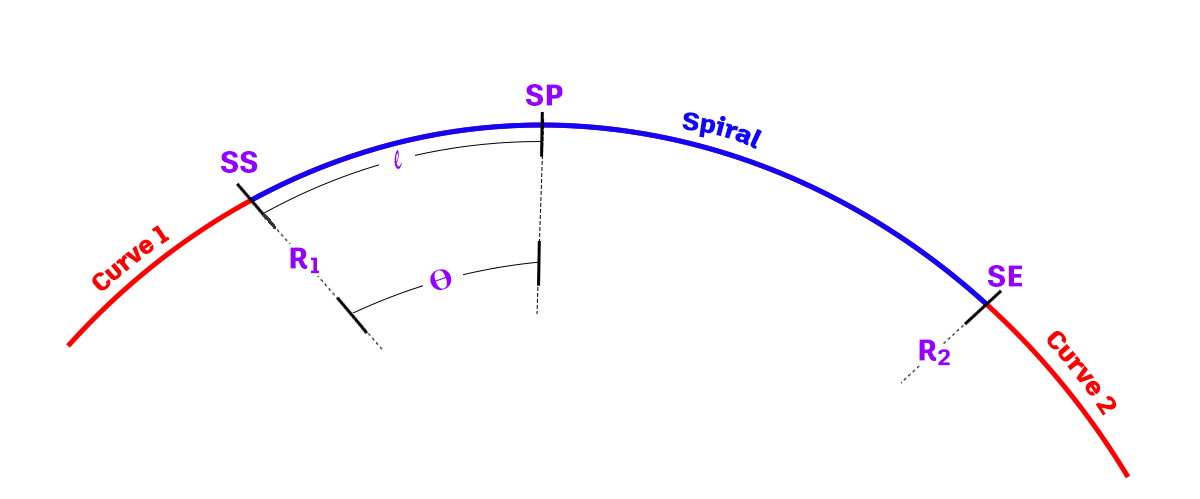
Následující ilustrace ukazuje různé parametry přechodnice:

Parametr přechodnice	Popis
R₁	Poloměr oblouku 1.
R₂	Poloměr oblouku 2.
SS	Počáteční pozice přechodnice.
SE	Koncová pozice přechodnice.
SP	Bod přechodnice při délce oblouku l.
Θ	Středový úhel v bodu přechodnice při délce oblouku l.
l	Délka oblouku od počáteční pozice přechodnice podél přechodnice.
L	Celková délka oblouku přechodnice mezi počáteční a koncovou pozicí přechodnice.

Složená přechodnice

Složená přechodnice poskytuje přechod mezi dvěma kruhovými oblouky s různými poloměry. Existují dvě složené přechodnice: jednoduchá a složená. Složená přechodnice se skládá z oblouku složeného ze dvou jednoduchých přechodnic. Obsahuje dvě rozpětí, přičemž každé z nich je jednoduchá přechodnice, která se plynule tečně spojuje se sousední přechodnicí. To umožňuje zajistit spojitost funkce zakřivení a poskytuje způsob zavedení hladkých přechodů do klopení vozovky.

Klotoida

Aplikace Autodesk Civil 3D sice podporuje několik typů přechodnic, ale nejčastěji používaným typem přechodnice je klotoida. Klotoidová přechodnice se používá na celém světě v projektech silnic i železničních tratí.

Jako první ji prozkoumal švýcarský matematik Leonard Euler. Funkce křivosti klotoidy je lineární závislostí křivosti na délce (na vzdálenosti od bodu nula (0)), kde se přechodnice dotýká tečny. Křivost klotoidy roste lineárně, dokud neodpovídá křivosti přilehlého oblouku v bodu, kde se přechodnice a oblouk stýkají.

Na rozdíl od jednoduchého oblouku také zachovává spojitost lokální křivosti, která nabývá na důležitosti pro vozidla při vyšších rychlostech.

Vzorec

Klotoidní přechodnice lze vyjádřit následujícími vzorci:

Kde:

Θ= Středový úhel v bodu přechodnice při délce oblouku l.
l = Délka oblouku podél křivky.

Pro referenci se podívejte na diagram výše.

Plochost přechodnice:

Celkový úhel přepínaný přechodnicí:

Délka tečny v bodu přechodnice-oblouk z bodu tečna-přechodnice je:

Tečná vzdálenost odsazení v bodu přechodnice-oblouk z bodu tečna-přechodnice je:

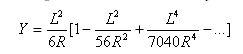
Blossova přechodnice

Místo použití klotoidy lze jako přechod použít Blossovu přechodnici. Tato přechodnice má před klotoidou výhodu v menším posunu P, proto je přechod delší a s větším prodloužením přechodnice (K). Tento faktor je důležitý při návrhu kolejové tratě.

Vzorec

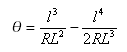
Blossova přechodnice může být vyjádřena jako:

Další základní výrazy:

Délka tečny v bodu přechodnice-oblouk z bodu tečna-přechodnice je:

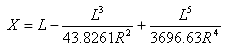
Tečná vzdálenost odsazení v bodu přechodnice-oblouk z bodu tečna-přechodnice je:

Sinusoidy

Tyto oblouky představují konzistentní průběh zakřivení a lze je použít k přechodu mezi 0 a 90 stupni tečných odklonění. Sinusoidy však nejsou příliš často používány, protože jsou strmější než skutečná přechodnice a je tudíž obtížné je zarovnat a vymezit.

Vzorec

Sinusoidy mohou být vyjádřeny jako:

Kde:

Θ= Středový úhel v bodu přechodnice při délce oblouku i.
l = Délka oblouku podél křivky.

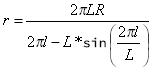
Pro referenci se podívejte na diagram výše.

kde písmeno r značí poloměr zakřivení v daném bodu.

Oblouk sinusové půlvlnné přechodnice

Tento tvar rovnice je běžně používán v Japonsku pro návrh železnic. Tento oblouk je užitečný v situacích, kdy potřebujete efektivní přechod ve změně křivosti pro malé úhly odklonění (co se týče dynamiky vozidla).

Vzorec

Oblouky sinusových půlvlnných přechodnic mohou být vyjádřen jako:

Kde a x je vzdálenost od počátku k libovolnému bodu oblouku a měří se podél (prodloužené) počáteční tečny; X je celkové X na konci přechodového oblouku.

Další základní výrazy:

Délka tečny v bodu přechodnice-oblouk z bodu tečna-přechodnice je:

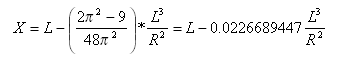
Tečná vzdálenost odsazení v bodu přechodnice-oblouk z bodu tečna-přechodnice je:

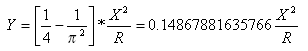
Kubické paraboly

Kubické paraboly konvergují pomaleji než kubické přechodnice, díky čemuž jsou oblíbené při projektování železnic a dálnic.

Vzorec

Minimální poloměr kubické paraboly

Poloměr v libovolném bodu kubické paraboly je:

Kde: Θ= Středový úhel v bodu přechodnice při délce oblouku .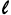

Pro referenci se podívejte na diagram výše.

Kubická parabola dosahuje nejmenšího r v bodu:

Proto

Poloměr kubické paraboly se zmenšuje od nekonečna až po při úhlu 24 stupňů, 5 minut a 41 vteřin a dále se začíná znovu zvětšovat. Díky tomu jsou kubické paraboly bezúčelné pro odklonění větší než 24 stupňů.

Kubická (JP)

Tato přechodnice je vyvinuta pro požadavky uživatelů v Japonsku. Bylo vyvinuto několik aproximací klotoidy pro použití v situacích, kdy je potřeba přizpůsobit malý úhel odchylky nebo velký poloměr. Jedna z těchto aproximací, použitá pro projekty v Japonsku, se nazývá kubická (JP).

Vzorec

Kubická přechodnice (JP) může být vyjádřena jako:

Kde X= délka tečny v bodu přechodnice-oblouk z bodu tečna-přechodnice

Tento vzorec lze také vyjádřit jako:

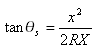
Kde je středový úhel přechodnice (zobrazeno v ilustraci jako i1 a i2)

Další základní výrazy:

Délka tečny v bodu přechodnice-oblouk z bodu tečna-přechodnice je:

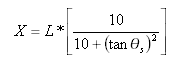
Tečná vzdálenost odsazení v bodu přechodnice-oblouk z bodu tečna-přechodnice je:

Kubická parabola NSW

Jedná se o typ upravené kubické paraboly, která splňuje požadavky norem australského Nového Jižního Walesu.

Vzorec

Kubickou parabolu NSW lze vyjádřit následovně:

Kde:

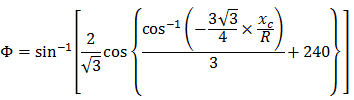
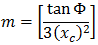
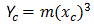
Φ = úhel mezi koncovou radiální čárou v poloměru R a na kolmé čáře a mezi počáteční tečnou
R = poloměr oblouku
X_c = celková hodnota X dané přechodnice
Y_c = celková hodnota Y dané přechodnice

Bikvadratické (Schrammovy) přechodnice

Bikvadratické (Schrammovy) přechodnice mají nízké hodnoty svislého zrychlení. Obsahují dvě paraboly druhého stupně, jejichž poloměry se mění jako funkce délky oblouku (l).

Vzorec jednoduchého oblouku

Zakřivení první paraboly:

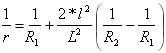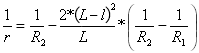pro