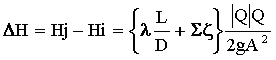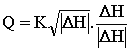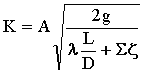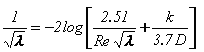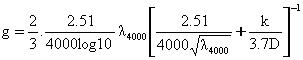Para fines de modelado, InfoWorks WS Pro subdivide los vínculos.
- dos nodos terminales ("i" y "j")
- longitud, L (m)
- diámetro interno, D (mm)
- coeficiente de fricción,λ
- suma de los coeficientes de pérdida de altura piezométrica local, ζ
El coeficiente de fricción se utiliza para calcular la pérdida de altura piezométrica a lo largo de una tubería. En el motor de simulación de InfoWorks, la pérdida de altura piezométrica siempre se calcula mediante la fórmula de Darcy Weisbach.
donde:
y: Q > 0 si Hj > Hi Q es negativo si Hj < Hi |
Para el método "orientado a nodos", esta ecuación se suele escribir como:
donde:
|
K es la medida de la capacidad de la tubería. K depende del valor del número de Reynolds Re .
donde:
|
Puede introducir un coeficiente de fricción en el formato de una de las tres fórmulas de fricción:
- Darcy-Weisbach
- Hazen Williams
- Colebrook-White
A continuación, InfoWorks convierte el coeficiente de fricción mediante los métodos que se describen a continuación.
Darcy-Weisbach
El parámetro λ introducido por el usuario se utiliza directamente. λno tiene dimensiones.
Hazen Williams
La fórmula de fricción de Hazen Williams:
donde: m = 4,8704 n = 1,852 C es el coeficiente de fricción |
InfoWorks utiliza la siguiente relación para convertir C al coeficiente de fricción de Darcy Weisbach λ:
|
El coeficiente de Darcy-Weisbach equivalente depende del número de Reynolds para el caudal en cada tubería y se vuelve a evaluar en cada estimación de la simulación.
Colebrook-White
El usuario puede decidir especificar la rugosidad interna K de Colebrook White.
El factor de fricción equivalente de Darcy-Weisbach, λ, se modela en el diagrama de Moody, depende del número de Reynolds (Re) para el caudal en cada tubería y se vuelve a evaluar en cada estimación de la simulación.
En el caso de Re >= 4000, InfoWorks resuelve la ecuación de Colebrook-White de forma iterativa para convertir la rugosidad interna k especificada en el coeficiente de fricción de Darcy-Weisbach con una precisión del 0,1 %:
|
En el caso de Re < 4000 existen dos métodos para modelar el diagrama de Moody en la zona crítica entre el caudal laminar y la zona de transición/turbulento.
- Splines de interpolación cúbicos
- CW-Moody modificado (valor constante)
El método CW-Moody modificado es el más estable numéricamente y, por este motivo, se establece como método por defecto en el cuadro de diálogo Opciones de simulación. Aunque esta opción puede sobrestimar el factor de fricción, esto generalmente solo ocurre para caudales de tubería bajos y no es probable que los efectos hidráulicos sean importantes.
Splines de interpolación cúbicos
En el caso de 2000 < Re < 4000, una interpolación polinómica cúbica que utiliza métodos de spline cúbica estándar para igualar el factor de fricción laminar en Re = 2000, el valor derivado de Colebrook-White en Re = 4000(λ 4000) y sus gradientes respectivos:
donde:
|
En el caso de Re <= 2000, el factor de fricción se calcula a partir de la fórmula de Hagen-Poiseuille para el caudal laminar:
|
CW-Moody modificado (valor constante):
En el caso de 2000 < Re < 4000, se impone un valor constante igual al factor de fricción calculado a partir de la ecuación de Colebrook-White con un número de Reynolds de 4000:
|
En el caso de Re <= 2000, el factor de fricción es el máximo de la fórmula Hagen-Poiseuille para el caudal laminar y el valor constante anterior con un valor de corte máximo de 8 para Re<= 8.
|