Atividade 4: Resolver a análise e analisar os resultados

Em um estudo de Tensão estática não linear, a solução é calculada sobre diversos incrementos. Neste tutorial, a carga de pressão na viga é aplicada gradualmente ao longo de 60 passos, permitindo visualizar o efeito da carga ao longo do tempo.

Nesta atividade, você

• Resolver o estudo

• Determinar se a viga é susceptível de colapsar

• Identificar quando o Fator de segurança cai abaixo de 1

• Revise o resultado da tensão de Von Mises para ver como as tensões mudam quando a viga de suporte é carregada

• Examine o resultado do Deslocamento para identificar quando o deslocamento começa a aumentar exponencialmente.

  

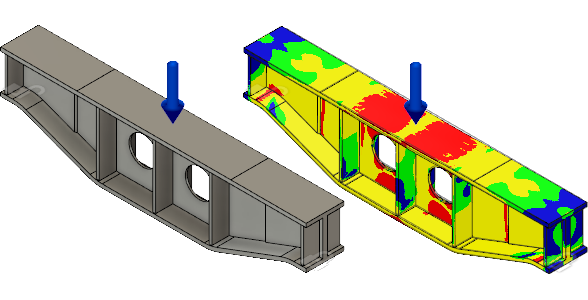
  Suporte do modelo de viga com restrições e cargas aplicadas (esquerda) e o resultado do fator de segurança estática não linear (direita).

Pré-requisitos

• A atividade 3 foi concluída.

Passos

1. Resolva o estudo.

   1. Clique no (Espaço de trabalho de simulação > guia Setup > painel Resolver > Resolver) para abrir o diálogo Resolver.
      
      Observação: O ícone de pré-verificação mostra uma marca de seleção verde do , que indica que não há avisos e que o modelo está pronto para resolver.
   2. Selecione o estudo a ser resolvido.
   3. Clique em Solucionar 1 estudo para executar a análise e fechar a caixa de diálogo.

      Observação: A criação de malha e a resolução da análise podem levar vários minutos.

   4. Quando a análise for concluída, clique em Fechar para fechar a caixa de diálogo Status do trabalho.

      A guia Resultados é aberta automaticamente, para que você possa visualizar os resultados.

2. Visualize os resultados do Fator de segurança e determine se a viga pode colapsar sob a carga aplicada.

   1. O resultado do Fator de segurança na etapa 60 é exibido na primeira vez que a solução de estudo é concluída. No entanto, se você executar novamente a solução, o resultado visualizado mais recentemente será mantido na conclusão. Se necessário, selecione Fator de segurança na lista suspensa de resultados junto à legenda.
      
      
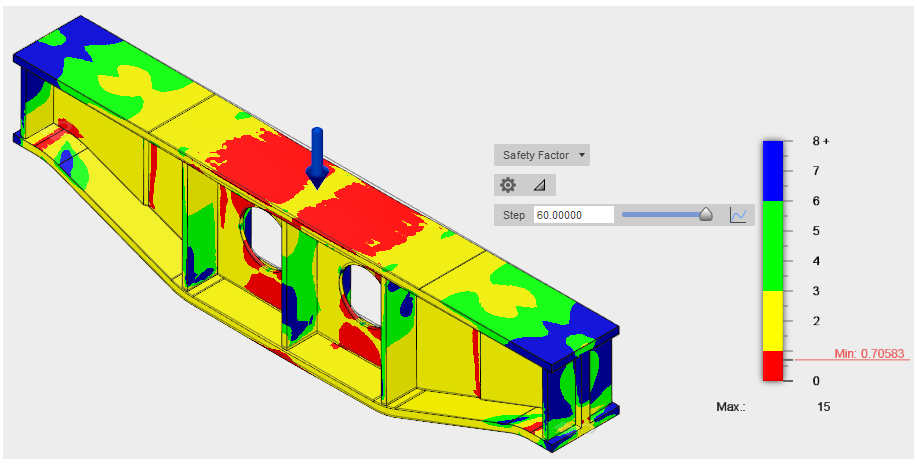
   2. Arraste o controle deslizante para frente e para trás para ver como o fator de segurança varia conforme a carga aumenta. A carga aumenta linearmente durante a simulação a uma taxa de 5 kN por etapa (5 kN * 60 etapas = 300 kN).

      Nota: o fator de segurança mínimo é de aproximadamente 0,7, indicando que a resistência ao escoamento do material foi significativamente excedida. Além disso, uma grande parte da peça de contorno é vermelha. Portanto, a deformação permanente certamente ocorreu e a viga está em risco de colapsar sob a carga aplicada.

3. Utilize a Plotagem de resultados transitórios para identificar quando o fator de segurança cai abaixo de 1,0.

   1. Na área de legenda de plotagem, clique no ícone Gráfico 2D à direita do controle deslizante Etapa.

      Dica: Clique e arraste a barra de título Plotagem de resultados transitórios para realocar a janela de plotagem. Também é possível clicar e arrastar o canto inferior direito da janela para redimensioná-la.

   2. Clique e arraste a linha do marcador de tempo no gráfico para localizar o ponto no qual o fator de segurança cai para 1,0.
      
      
      
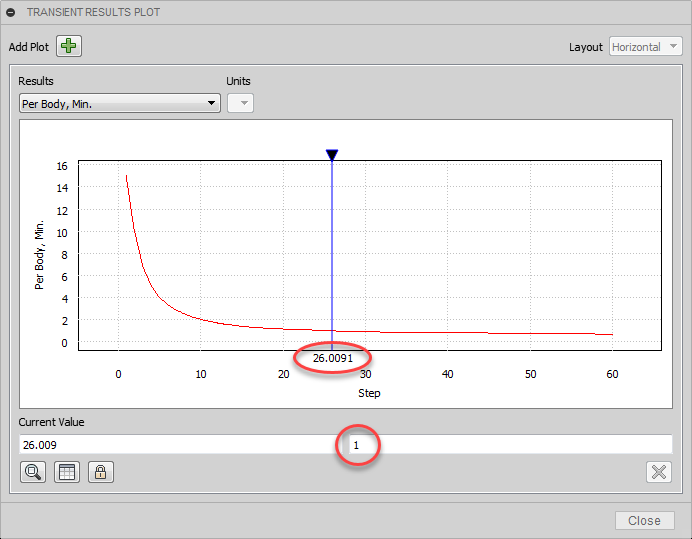
      Observe que o fator de segurança cruza por 1,0 na 26ª etapa de cálculo. A partir desta observação, podemos concluir que a carga se torna crítica em cerca de 43% da carga aplicada, ou 130 kN:

      (Etapa 26 / 60 Etapas = 0.433 e 0.433 * 300 kN = 130 kN.)

   3. Clique em Fechar para fechar o gráfico.

4. Visualize o resultado da tensão de Von Mises para ver como as tensões mudam quando a viga de suporte é carregada.

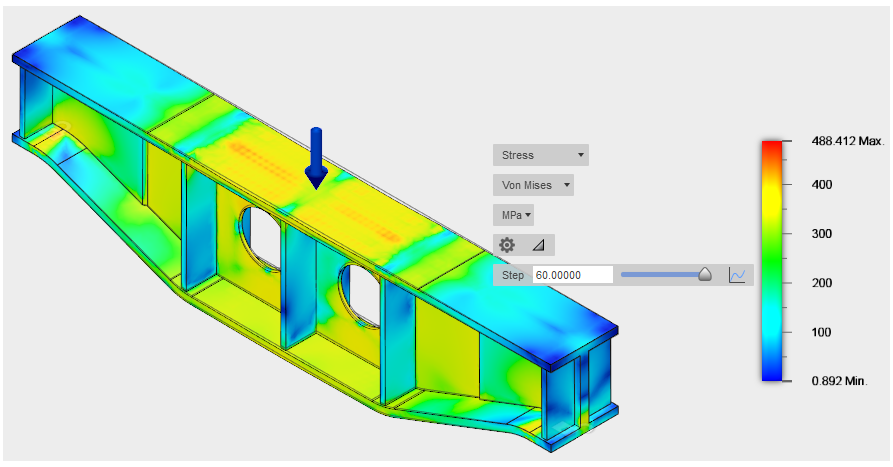
   1. Selecione o resultado de Tensão na lista suspensa. O tipo de tensão padrão exibido é von Mises.
   2. Arraste o controle deslizante de degrau para ver como as tensões mudam quando a viga de suporte é carregada.
      
      
   3. Clique no ícone Plotagem 2D para visualizar a Tensão de Von Mises máxima em todo o histórico de carga.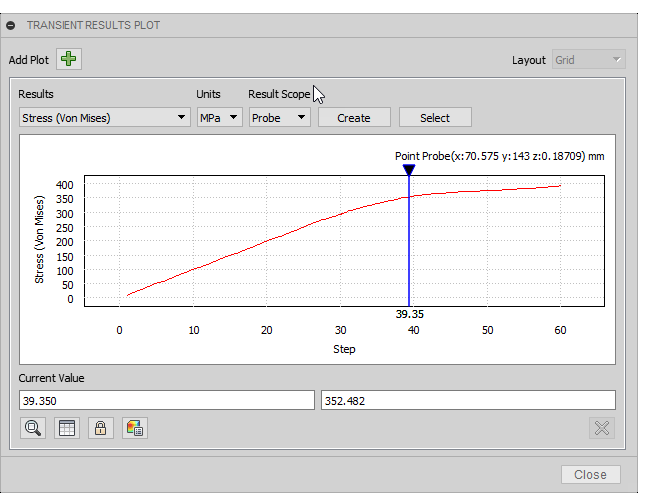
      
      
      
      Aqui, o controle deslizante é posicionado para mostrar o ponto no qual começa a escoamento inicial, que é de aproximadamente 233,7 MPa para este material.

      Observe a resposta não linear da viga. À medida que a carga aumenta, a viga começa a ceder. Uma vez que a escoamento é iniciada, a taxa de aumento de tensão diminui. Durante esse processo, o material endurece o trabalho e se torna mais forte. Se simplesmente executássemos um estudo de tensão estática linear na viga, veríamos apenas as tensões na viga no final da análise. As tensões previstas seriam muito maiores porque se presume que o material permaneça em sua rigidez elástica (Módulo de Young).

      Dica: Se você observar as propriedades básicas do material, verá que a Resistência ao escoamento é significativamente maior do que a Tensão de escoamento inicial mostrada nas Propriedades avançadas (não lineares). O motivo é que a tensão de escoamento básica é o ponto no qual a rigidez do material é deslocada 0,2% do comportamento linear. Esse deslocamento de 0,2% é a base típica das classificações de resistência de escoamento do material. A tensão de escoamento inicial não linear é o ponto no qual a rigidez começa a se desviar do Módulo de Young. Você pode ver que a inclinação da curva de tensão muda mais rapidamente quando a resistência ao escoamento básica (cerca de 345 MPa) for ultrapassada.

   4. Clique em Fechar para fechar a plotagem 2D.

5. Visualize o resultado de Deslocamento para identificar quando o deslocamento começa a aumentar exponencialmente.

   1. Selecione o resultado de Deslocamento na lista suspensa próxima à legenda.

      O deslocamento total é exibido por padrão. Ao contrário dos estudos lineares, a forma deslocada verdadeira é exibida por padrão para estudos não lineares. Isto é, a distorção não é exagerada (embora você possa escolher fazê-lo). Portanto, o deslocamento parece menos grave do que o que você pode estar acostumado a ver em uma análise de tensão estática linear. Não deixe que isso te engane. Observe os números reais de deslocamento.

      
      
      
      
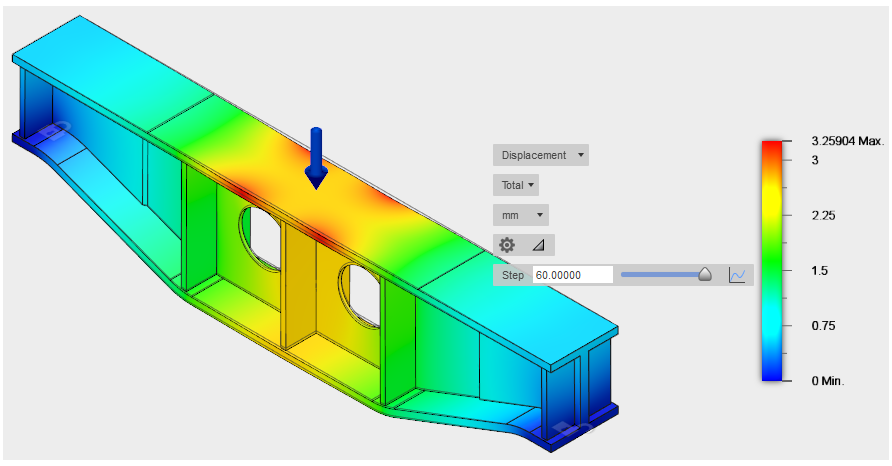
      Como você pode esperar, o deslocamento máximo ocorre perto do meio da extensão da viga e no flange superior, onde a carga é aplicada.
   2. Clique no ícone Plotagem 2D para visualizar o Deslocamento total máximo em todo o histórico de carga.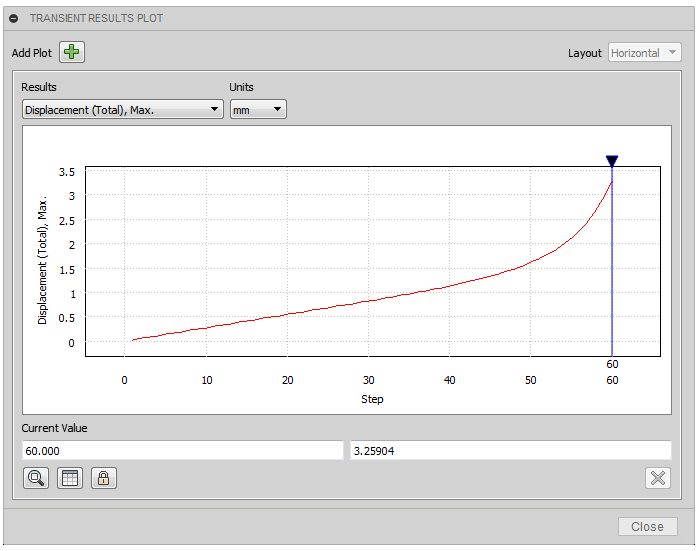
      
      
      
      Observe como o deslocamento começa a aumentar exponencialmente na etapa de cálculo de 45º. No final da simulação, a inclinação é bastante íngreme. As tensões que excedem a resistência ao escoamento se propagam e penetram mais profundamente, afetando uma quantidade maior do volume da viga à medida que o estudo avança. Portanto, o material não é mais capaz de suportar a carga aplicada. Claramente, a viga está na beira do colapso.

Resumo da atividade 4

Nesta atividade, você

• Resolveu o estudo
• Determinado se a viga é susceptível de colapsar
• Identificado quando o Fator de segurança cai abaixo de 1
• Foi revisado o resultado da tensão de Von Mises para ver como as tensões mudam quando a viga de suporte é carregada
• Examinado o resultado de Deslocamento para identificar quando o deslocamento começa a aumentar exponencialmente.