Fiber orientation effect on thermal conductivity

This option considers the fiber orientation effect on the thermal conductivity.

For a polymer composite with fibers fully aligned in the first direction, the three diagonal components of the anisotropic thermal conductivity tensor have the forms as [1][2]

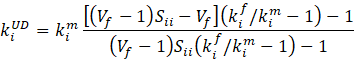
where:

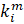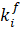• and are the thermal conductivity of the matrix and fiber, respectively, in the i-th direction,
• is the fiber volumetric fraction,
• , ,
• ,
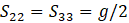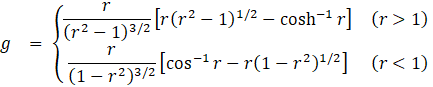• is the fiber aspect ratio.

Orientation averaging is then applied to obtain the thermal conductivity tensor of the composite with a given fiber orientation.

The finite element form of the energy equation is modified accordingly to incorporate the contribution of the fibers.

As the thermal conductivity data in the material database are typically the bulk values of a composite with a certain fiber orientation, the matrix thermal conductivity 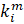is decomposed from the database value with an assumed fiber orientation.

Reference

1. Zheng, R. and Kennedy, P.K., Anisotropic thermal conduction in injection molding. The Polymer Processing Society 22nd Annual Meeting (2006).
2. Chen, C.-H., & Wang, Y.-C., Effective thermal conductivity of misoriented short-fiber reinforced thermoplastics. Mechanics of Materials, 23(3):217–228 (1996).