Head-Table machine tool (DMG_DMC_80_U2_DuoBlock) without collinear vectors of rotation (the axes of rotation are not parallel to the axes of the global coordinate system).

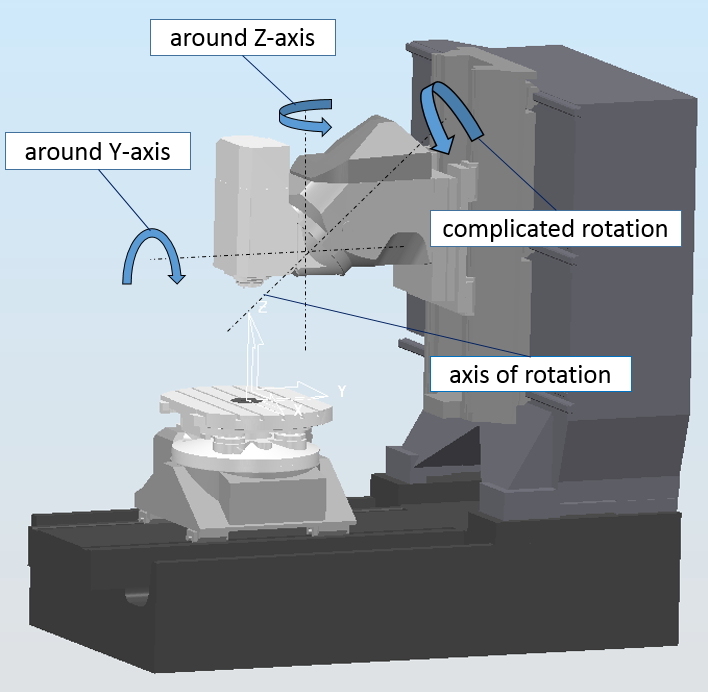
Such rotation is complicated because it consists of two rotational movements (around Z-axis and around Y-axis).

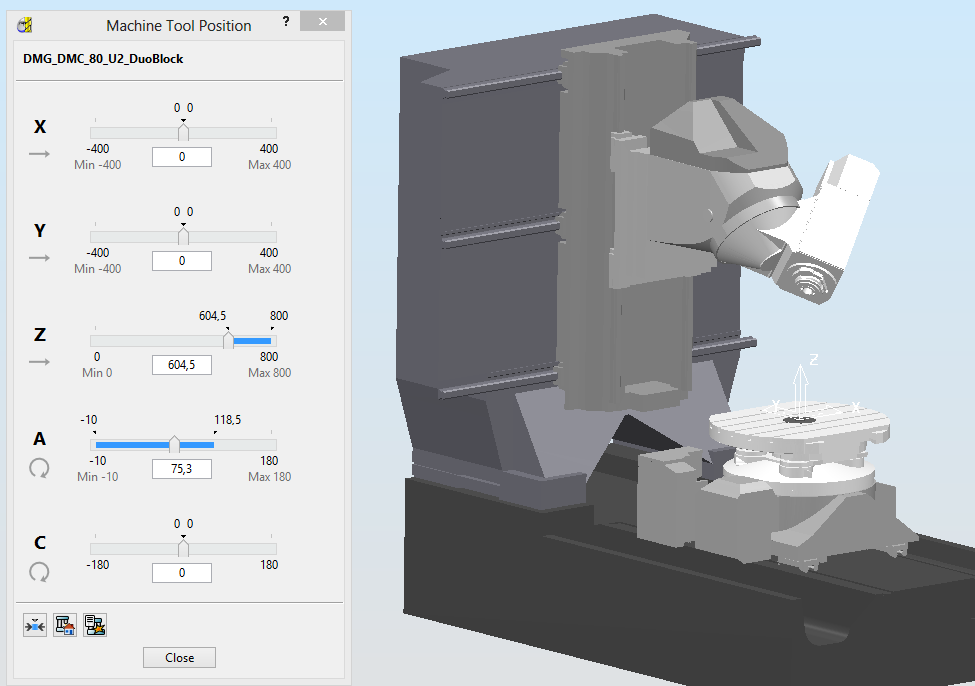
It is necessary to find the centre of rotation and the direction of motion. Consider the plane of rotation.

Let's create a new local coordinate system (LCS-1) in the centre of the table X=0 Y=0 Z=0. We then create some simple arcs where we can note the exact location of the centre of rotation:

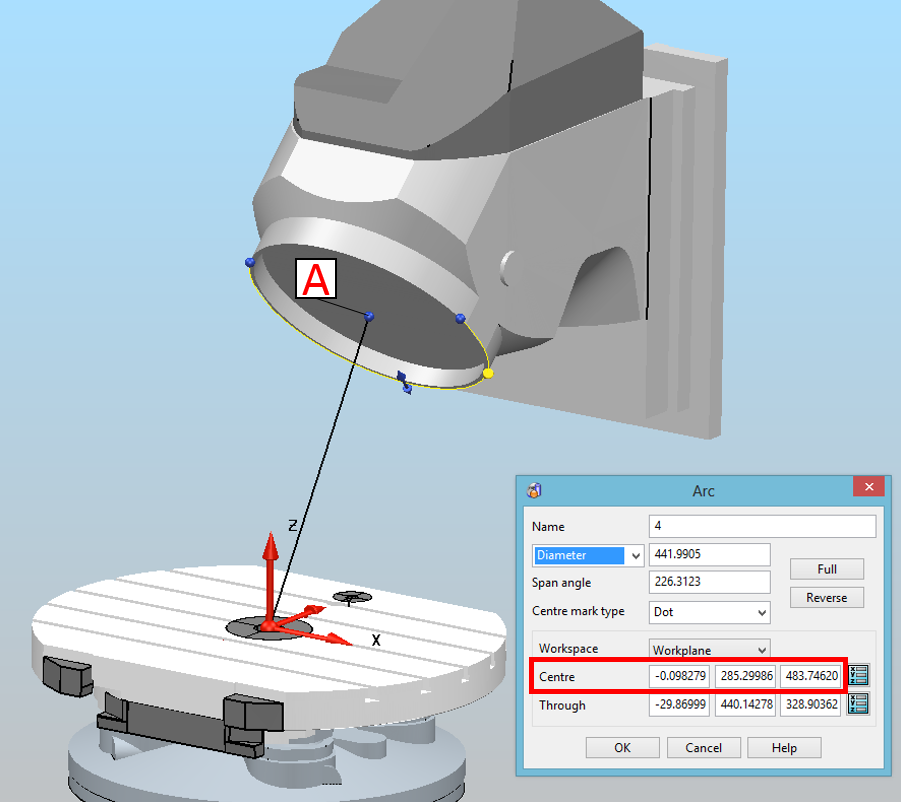
Double clicking on the arc (the point A) gives us the center of rotation with coordinates: X=-0.098279 Y=285.29986 Z=483.74620.

We use these coordinates to define the center of rotation.

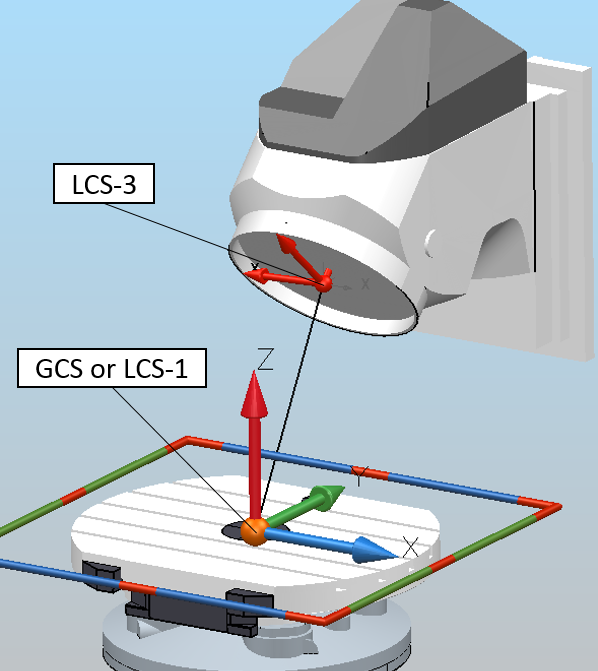
At the centre of rotation (point A), we create a local coordinate system (LCS-2) oriented like the global coordinate system.

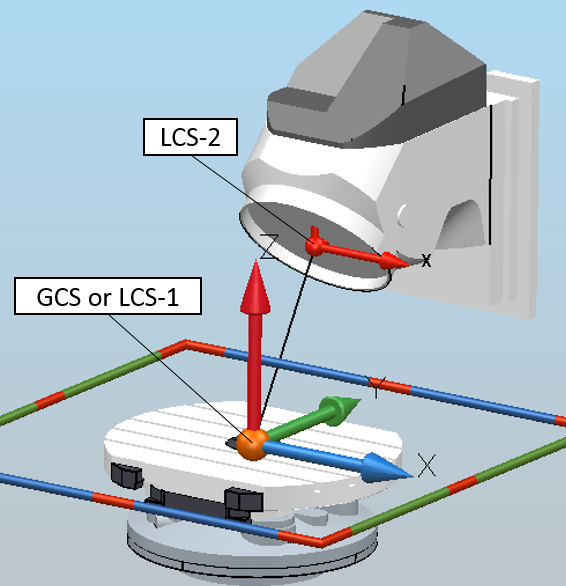
Then, we create a local coordinate system (LCS-3) at point A, oriented perpendicular to the created arc (Z-axis should be perpendicular to the created arc):

By using activated LCS-3 create a short line (start point x=0; y=0; z=0; and end point x=0; y=0; z=1)

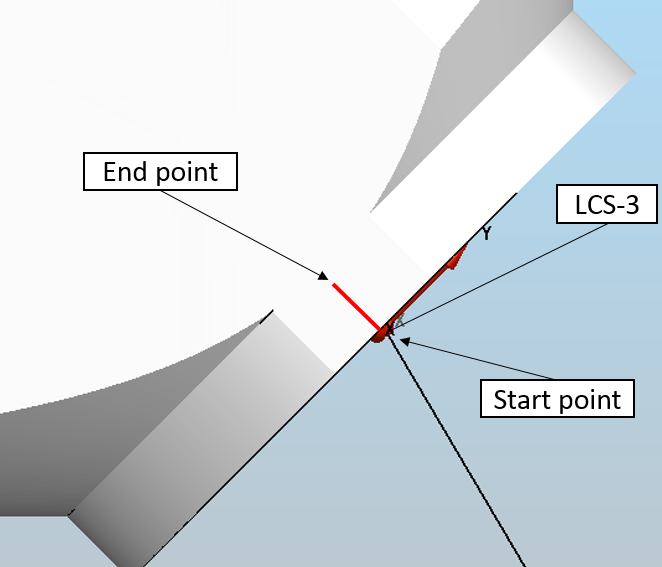
Then we activate LCS-2 and double click on the short line

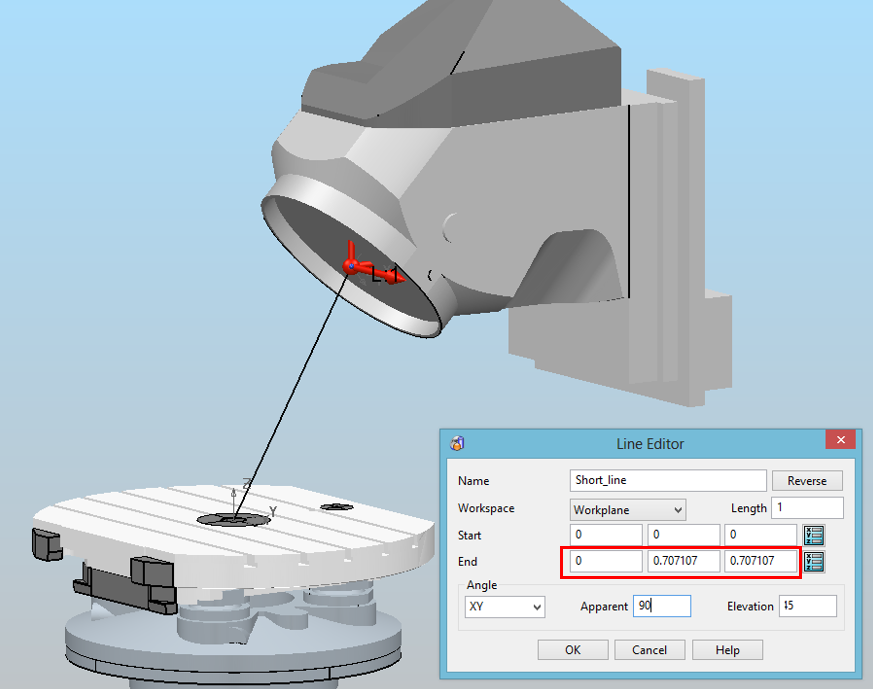
Where I=0; J=0.707107; K=0.707107. We find the direction of movement.

See screenshot below:

If the elevation is 45 degrees then we can use I=0; J=1; K=1.

Finally, use PowerMill and PostProcessor for testing the MTD (check the start and end point, correct position of all parts of machine, collision detection).