Sections with a corrugated web are I-sections with thin-walled, corrugated webs. They are sections from the SIN section family, or with user-defined dimensions.
Members with a corrugated web can be designed only in accordance with the Polish steel code.
The following parameters specify a section with a corrugated web:
- Label - Assigns a label (name) to a section. (Robot assigns automatically a standard label for the section, such as, WTB 1000 - 300 x 15.)
- Color - Specifies a color for the section.
- Specify a section:
- From the database:standard sections with identical flanges (b 1 =b 2 , t f1 = t f2 ) and the following symbols of the web thickness:
- A - 2 mm (standard section label: WTA ...)
- B - 2.5mm (standard section label: WTB ...)
- C - 3 mm (standard section label: WTC ...)
- S (Standard section label: WTS ...)
- t w - Web thickness
- h - Web height
- b 1 - Width of the upper flange
- t f1 - Thickness of the upper flange
- b 2 - Width of the lower flange
- t f2 - Thickness of the lower flange
- moreover, in the calculation of section properties the following variables are used:
- f - Wave amplitude
- m - Projected length of a wave
- s - Developed length of a wave
All dimensions are those of the SIN section family; therefore, the fields for defining the dimensions are unavailable.
- With user-defined values:
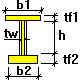
- Section type - Set of options for selecting an appropriate section type.
- Gamma angle - Specifies the gamma angle of a section.
Geometrical properties
Total section height: H = h + t f1 + t f2
Cross-sectional area of flanges
Af = b1 * tf1 + b2 * tf2
Cross-sectional area of a web
Aw = h * tw
Total section area
A = Af + Aw
Cross-sectional areas effective for shear
Ay = b1 * tf1 + b2 * tf2 - Cross-sectional area of flanges
Az = Aw * m / s - Reduced cross-sectional area of the web
Properties calculated without considering the web
Static moment
S = b1 * tf1 * (h + tf2 + tf1 / 2) + b2 * tf2 * tf2 / 2
Position of the section centroid

Moments of inertia about Y and Z axes, respectively, of a section made only of flanges
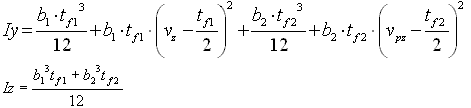
Torsional moment of inertia
Self-weight
G= Gf +Gw
G f = r s * A f * l
Gw = r s * Aw * lw = r * Aw * l/m * s
where:
A f - Cross-sectional area of flanges
A w - Cross-sectional area of the web
r s - Unit weight of steel
l - Member length
Iw - Developed length of the web plate: lw = l / m * s
m - Projected length of a wave
s - Developed length of a wave.
