There are several types of iterative solvers.
Iterative ICCF
This method is recommended for large-scale problems with a small number of right-hand sides.
- Memory use: high.
- Disk use: not used.
- Speed estimation: fast (for well-conditioned problems).
- Quantity of equations:15 000 - 1,000,000 equations and more.
- Supported analyses: linear statics, modal analysis, buckling.
- Available analysis limitations: N/A.
- Other limitations:
- The correctness of structure restrictions is not checked.
- Slow convergence if some problems are incorrectly conditioned.
Iterative diagonal
This method is recommended for large-scale problems with a small number of right-hand sides.
- Memory use: minimal
- Disk use: minimal
- Speed estimation: slow
- Quantity of equations:15 000 - 1,000,000 equations and more.
- Supported analyses: linear statics, modal analysis, buckling.
- Available analysis limitations: N/A
- Other limitations:
- The correctness of structure restrictions is not checked.
- Slow convergence if some problems are incorrectly conditioned.
Iterative Gauss-Cholesky
This method is recommended for large-scale problems with a small number of right-hand sides, when there's is not enough RAM to use the ICCF method.
The verification of each element matrix is conducted by means of the Vinget regularization procedure 12.
- Memory use: minimal
- Disk use: minimal
- Speed estimation: slow
- Quantity of equations:15 000 - 1,000,000 equations and more.
- Supported analyses: linear statics, modal analysis, buckling.
- Available analysis limitations: N/A
- Other limitations:
- The correctness of structure restrictions is not checked.
- Slow convergence if some problems are incorrectly conditioned.
Iterative multilevel ICCF
This method is recommended for large-scale problems with a small number of right-hand sides. It shows a quicker convergence than the iterative ICCF method.
- Memory use: high
- Disk use: minimal
- Speed estimation: quick for well-conditioned problems
- Quantity of equations:15 000 - 1,000,000 equations and more.
- Supported analyses: linear statics, modal analysis, buckling.
- Available analysis limitations: available structure types: 3D (bar, shell, solid and all special finite elements), 2D frame.
- Other limitations:
- The correctness of structure restrictions is not checked.
- Less stable convergence, in a few cases.
Iterative multilevel diagonal
This method is considerably slower than the iterative multilevel ICCF. However, it requires much less RAM memory.
The Smoothing method 2 usually requires fewer iterations compared to the iterative multilevel ICCF method.
The verification of each element matrix is conducted by means of the Vinget regularization procedure 1,2.
- Memory use: minimal
- Disk use: minimal
- Speed estimation: slow
- Quantity of equations:15 000 - 1,000,000 equations and more.
- Supported analyses: linear statics, modal analysis, buckling.
- Available analysis limitations: available structure types: 3D (bar, shell, solid and all special finite elements), 2D frame.
- Other limitations:
- The correctness of structure restrictions is not checked.
Iterative multilevel Gauss-Cholesky
This method is considerably slower than the iterative multilevel ICCF. However, it requires much less RAM memory.
The Smoothing method 2 usually requires fewer iterations compared to the iterative multilevel ICCF method.
The verification of each element matrix is conducted by means of the Vinget regularization procedure 1,2.
- Memory use: minimal
- Disk use: minimal
- Speed estimation: medium (for well-conditioned problems)
- Quantity of equations:15 000 - 1,000,000 equations and more.
- Supported analyses: linear statics, modal analysis, buckling.
- Available analysis limitations: available structure types: 3D (bar, shell, solid and all special finite elements), 2D frame.
- Other limitations:
- The correctness of structure restrictions is not checked.
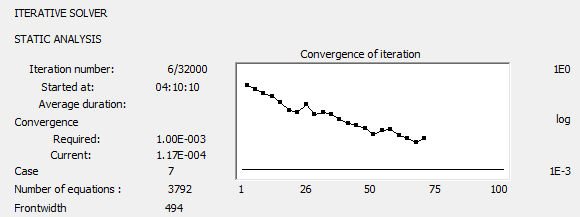
Iterative Method calculations
The calculations dialog for the Iterative method shows the convergence process of the iterative method if the user defined level of accuracy is achieved, or if the process is divergent.
- Number of the current iteration / maximum number of iterations.
- Required accuracy.
- Accuracy of the current iteration.
- Number of equations.
- Frontwidth.