Calculations due to punching - description

Calculation of Critical Area And Critical Circumference

The shape of the critical area depends on the support geometry or support head, inclination angle of the surface subjected to shearing, as well as the position with respect to slab edges and corners. Shape and size of the critical area are stricly determined in the code, but for every code calculations consist in determining the area subjected to action of a punching force. In calculation of this, zone edges of slab and of openings are considered. The table displays the length of the u critical circumference. Note that the effect of openings on the length of the critical circumference is considered in the program.

A = u * d

where:

A - Critical area

u - Length of the critical circumference

d - Usable height of the slab section.

Calculation of Limit Punching Forces or Limit Stresses

This stage of calculations includes determining maximal values of puching force allowed by the code or maximal stresses that can be carried by a concrete section. The limit (maximal) force is a product of the critical area and stresses allowed by the code.

Q_adm = τ * A

where:

Q_adm - Admissible punching force

τ - Admissible stress

A - Critical area.

Calculation of Punching Forces or Stresses Resulting from External Impact

Each of the codes determines the manner how a force or stress caused by external impact should be received on the punching area. In the simplest case, calculations involve multiplication of a punching force by an appropriate factor, whereas in the most complicated ones, calculations of stresses considering acting moments are required. The table displays a value of the Q calculation designing force, obtained from the formula.

Q = τ * A

τ = V / A

(for ACI code)

where:

Q - Calculation designing force

τ - Stress on the critical area

V - Maximum punching force

Mx, My, V - Bending moments and the force at the gravity center of the critical area

Jx, Jy - Inertia moments of the critical area with respect to axes passing through its gravity center

γ _x , γ _y, c _x , c _y - Parameters depending on the geometry of the critical area [ACI 318 11.12.2.2].

For Eurocode EN 1992-1-1, based on point 6.4.3(3) calculations include eccentricity of force. The eccentricity is taken into account based on a factor defined by the Eurocode as coefficient β in equation (6.39). RSA at each time includes biaxial eccentricity. Because of that equation (6.39) is extended and has two independent parts for M_x/W_1x and M_y/W_1y.

Check of the Load Capacity Condition

This consists in comparing stresses or forces caused by external impact with limit values. There are three states possible.

• If calculated stresses are smaller than admissible for a concrete section, reinforcement is not required
• If stresses are greater than admissible for a concrete section and simultaneously smaller than admissible, reinforcement is required
• If stresses are greater than admissible stresses, then the slab section is too small.

When reinforcement is not required or when a slab section is too small, results are presented in a form of the maximal punching force (for calculations based on stresses, the force is calculated from stresses multiplied by the punching area) and the ratio of admissible force to equivalent acting force. If reinforcement is required, then calculations of the reinforcement needed are carried out by the program.

Calculation of Required Reinforcement

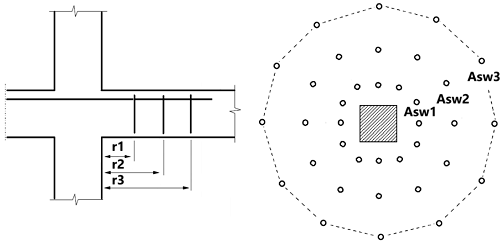
If stresses are greater than those admissible for a concrete section and simultaneously smaller than those admissible, then calculated punching reinforcement is necessary. Calculations are carried out according to the code guidelines concerning bar reinforcement. Required reinforcement area and range of a zone within which reinforcement is required are shown in the table on the Punching tab. Also available are punching force (for calculations based on stresses, the force is calculated from stresses multiplied by the punching area) and ratio of the load capacity with reinforcement considered to the equivalent acting force. The range of reinforcement zone is additionally presented in drawings. The table shows the following parameters.

L1, L2 - Reinforcement range from the member center in both perpendicular directions.

u - Length of reinforcement zone circumference according to code recommendations.

A - Total reinforcement area that should be distributed evenly around the column within the reinforcement zone determined by the lengths L1 and L2.

n x ϕ - Number and diameter of bars calculated on the basis of the total area and settings in the options for punching.

• When v_Ed < v_Rd,c punching shear reinforcement is unnecessary to carry on acting forces.
• When v_Ed > v_Rd,c and v_Ed < v_Rd,max punching shear reinforcement is necessary.
• In the last case where v_Ed > v_Rd,max the shear resistance is insufficient to carry on acting forces.

Based on point 6.4.3(3) calculations include eccentricity of force. Values Q and Q_adm are presented in the table in the dialog and the note represents design values of acting and resistance forces including the effects of eccentricity. The eccentricity is taken into account based on a factor defined by the Eurocode as coefficient β in equation (6.39). RSA at each time includes biaxial eccentricity. Because of that equation (6.39) is extended and has two independent parts for M_x/W_1x and M_y/W_1y. Q_adm depends on the state of design and represents admissible value based on v_Rd,c, v_Rd,s orv_Rd,max.

When v_Ed > v_Rd,c and v_Ed < v_Rd,max the shear reinforcement A_sw is calculated based on equation (6.52). The outermost perimeter of shear reinforcement u_out based on Eurocode requirements is calculated too. The assumption is that the maximum spacing of shear links in the tangential direction s_t equals 2*d. For each perimeter, reinforcement is the same except the situations where A _sw,min equation (6.11) is important. In that case, r, u, and A _sw are presented in the table in the dialog and the note.

r_i represent the radiuses of perimeters

u_i values lengths of perimeters.

A_sw shear reinforcement based on equation (6.52)

n x ϕ as above

Next values ​​ of r_i u_i A_sw represent values as on the picture below: