- 強制変位を使用すると、[大きさ]フィールドで指定した距離に基づいて、節点を並進または回転させることができます。この並進および回転は、[方向]領域で指定した任意のベクトルに沿って行えます。
- 解析のある時点における節点の変位は、強制変位に割り当てられた[大きさ]の値と、荷重曲線により与えられたその時点の乗数に基づいて決まります。詳細については、下記のヒントを参照してください。
- 強制変位は、有効範囲に基づいて削除できるほか、再度挿入することもできます。この機能は、時間に依存する境界条件など、モデルを解放する必要があるさまざまな状況で有効な手段となります。強制変位に関する有効範囲を指定する場合は、[アクティブな範囲]フィールドの横にある[データ]ボタンをクリックします。
- 強制変位で節点を移動するのに必要な力は、計算して出力することができます。反力の出力を有効にする場合は、「解析の設定と実行」>「非線形」>「解析パラメータ」>「出力結果を制御する」を参照してください。
この並進または回転の速度は、それが適用される荷重曲線により制御されます。変位は、速度を積分したものに等しくなります(d = integral V dt)。したがって適切な速度を基にすれば、変位と時間のグラフを計算することができます。変位と時間の関係を表すこのデータは、荷重曲線に入力します。速度が一定の場合は、次の式が成り立ちます。
d = d 0 + V*t
ただし、d 0 は初期位置、V は一定速度、t は時間を表します。速度が一定であれば、変位は時間に対して線形となるため、荷重曲線に対しては 2 つの点が与えられれば十分です。必要に応じて、各時間ステップごとに線形に補間されます。
解析中に加速の様子をシミュレートできるよう、その加速度での節点の変位を表す 2 次式で定義された荷重曲線を作成することができます。変位は、加速度を 2 回積分したものに等しくなります(d = double integral A dt)。したがって加速度を基にすれば、変位と時間のグラフを計算し、荷重曲線に入力することができます。加速度が一定の場合は次の式が成り立ちます。
d = d 0 + V 0 *t + 0.5*A*t^2
ただし、d 0 は初期位置、V 0 は初速度、A は一定の加速度、t は時間を表します。加速度が一定であれば、変位は時間に対して非線形であるため、荷重曲線に対し 2 つの点が与えられるだけでは不十分で、線形に補間しても加速度一定の曲線は得られません。理論に即した滑らかな加速度を実現するためには、荷重曲線上の時間ステップは、解析中に現れる最短の時間ステップよりもさらに短いことが必要です。図 1 を見てください。
|
変位 |
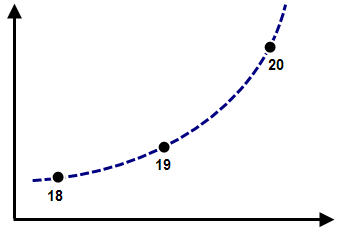
| (a) 理論上の加速度(破線の曲線)に従って、時間ステップ 18、19、および 20 での変位を荷重曲線に指定します。解析で同じ時間ステップが使用される場合の変位についても、理論上の加速度に基づいて計算が行われます。 |
|
変位 |
| (b)解析中に時間ステップ・サイズが縮小されると、中間の時間ステップ(ステップ 19 および 21)における変位は、荷重曲線のデータ ポイント(ステップ 18、20、および 22)を基にして線形に補間されます。時間ステップ 18 と 20 の間では、変位は線形になるため、速度は一定であり、したがって加速度は 0 となります。時間ステップ 20 と 22 の間でも、荷重曲線の補間により速度は一定であり、したがって加速度は 0 となります。時間ステップ 20 では速度が突然変化しているため、大きな力がかかり、収束に問題が生じる場合があります。 |
| 図 1: 加速度をシミュレートした変位荷重曲線 |
強制変位を適用する
節点、エッジ、サーフェス、またはパーツが選択されている場合、表示領域で右クリックし、[追加]プルダウン メニューを選択してください。[強制変位]コマンドを選択します。
強制変位に基づいて節点を並進または回転させるかどうかを指定する場合は、[タイプ]領域で適切なラジオ ボタンを選択します。当然ながら、回転させることができるのは、ビーム要素やシェル要素など、回転の自由度を持った要素の節点のみです。
選択した各項目に適用する強制変位の大きさを[大きさ]フィールドで指定し、強制変位の方向を[方向]領域で指定します。[スカラー X]、[スカラー Y]、[スカラー Z]のいずれかのラジオ ボタンを選択した場合は、その方向への並進または回転のみ拘束され、それ以外の方向には自由に移動できます。[ベクトル]ラジオ ボタンを選択した場合は、3 方向すべてに対して並進または回転が拘束されます。たとえば、大きさが -1 インチの強制変位を追加し、[スカラー Y]ラジオ ボタンを選択した場合、解析では Y 軸方向にのみ反力が作用します。X 軸方向または Z 軸方向には、節点は自由に移動できます。また、大きさが 1 インチの強制変位を追加し、[ベクトル]ラジオ ボタンを選択して、ベクトル(0,-1,0)を指定すると、解析では X 軸方向、Y 軸方向、および Z 軸方向に反力が作用します。X 軸方向および Z 軸方向への並進移動は 0 に維持されます。
大きさに対する乗数を指定するために使用する荷重曲線を[荷重ケース/荷重曲線]フィールドに指定します。[曲線]ボタンをクリックし、荷重曲線エディタで荷重曲線を定義します。荷重曲線は
[設定] [モデル設定]
[モデル設定] [パラメータ]
[パラメータ]
 [解析パラメーター]ダイアログでも定義できます。
[解析パラメーター]ダイアログでも定義できます。
ヒント
強制変位は、解析中のどの時点でも有効にすることができるため(後述するように有効範囲の生成時間を使用)、時刻 T において、節点が元の位置から、強制変位の大きさと荷重曲線乗数との積により定まる位置へ突然移動した場合、モデルは不安定になるかまたは予期せぬ結果を生じることになります。そのため強制変位では、時刻 T における荷重は荷重の大きさと荷重曲線乗数との積に等しい(D(T) = mag x LCM(T))という通常のルールは使用されず、時間ステップにおける運動は、強制変位に割り当てられた大きさと、荷重曲線乗数の変化分との積に等しい(ΔD(T) = mag x LCM(T)-LCM(T-1))というルールが使用されます。そのため、これら 2 つの荷重曲線は、強制変位の大きさとは無関係に、解析の開始後 2 秒間は節点が移動しない(その場に静止する)ことを示しています。
| 荷重曲線 1 | ||
| インデックス | 時間 | 乗数 |
| 1 | 0 | 5 |
| 2 | 2 | 5 |
| 3 | 2.5 | 6 |
| 荷重曲線 2 | ||
| インデックス | 時間 | 乗数 |
| 1 | 0 | 0 |
| 2 | 2 | 0 |
| 3 | 2.5 | 2 |
2 秒から 2.5 秒までの間に、荷重曲線 1 の乗数は 1 (= 6-5)だけ変化しています。荷重曲線に従うように割り当てられた強制変位の大きさが 5 mm の場合、節点は 2 秒から 2.5 秒までの間に 5 mm (= 5 mm x (6-5))移動します。
荷重曲線 2 を使用した場合は、2 秒から 2.5 秒までの間に乗数が 2 だけ変化しています。したがって、強制変位の大きさが 5 mm であれば、節点は計 10 mm (= 5 mm x (2-0))の距離を移動することになります。
その他の例として、別の強制変位が 2.25 秒の時点で有効になった場合(生成時間)を考えます。また、最初の 2.25 秒間は自由に移動できることから、2.25 秒の時点における X の変位は 0.3481 インチだとします。(モデル内の別の仮想的な荷重によるものとします。)強制変位の大きさを 0.1 インチとして荷重曲線 1 を使用すると、節点は X 方向に 0.3981インチ(= 0.3481 inch + 0.1 inch x (6-5.5)、ただし 5.5 は 2.25 秒の時点において補間された荷重曲線乗数)の位置まで移動します。
[アクティブな範囲]フィールドに数値を設定して、強制変位を有効範囲に割り当てます。ただし、同じ有効範囲に割り当てられた強制変位はすべて、同じ生成時間および消滅時間を共有します。強制変位をどの時点でモデルに割り当てるかは重要ではありません。有効範囲 1 に複数の強制変位が割り当てられた場合、それらの生成時間および消滅時間は同じです。
[アクティブな範囲]フィールドの横にある[データ]ボタンをクリックして、強制変位に対する有効範囲(期間)を指定します。スプレッドシートの[インデックス]の番号または行が、変位に割り当てられた有効範囲番号に対応します。[生成時間]列で、強制変位が荷重曲線に従い始める時刻を指定します。節点に対してはこの時点で、強制変位の大きさおよび方向が、現在の位置を基準として適用されます。[消滅時間]列で、強制変位が無効になる(解析から除外される)時刻を指定します。強制変位を再度有効にする場合は、[再生成インデックス]列に値を指定します。これにより、[インデックス]行が参照されます。強制変位は、このインデックスに対応する[生成時間]列に指定されている時刻に再び有効となります。
 時間
時間 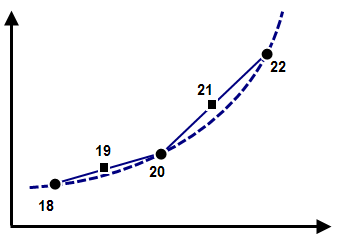 時間
時間