Pour affiner davantage ce processus, il est possible de dessiner une ellipse d'erreur standard. A l'aide d'une distribution F extraite de statistiques appliquées, une ellipse d'erreur d'une probabilité de 95 ou 99 % est créée. Cette ellipse présente une tangente d'arc sur les côtés du rectangle d'erreur, son orientation étant déterminée par un angle (t) et des axes orthogonaux auxiliaires (u-v). Les valeurs de la matrice de covariance sont à nouveau utilisées pour calculer l'angle t et les axes semi-majeur et semi-mineur associés.
Calculez tout d'abord les trois variables à utiliser dans les équations pour déterminer les axes semi-majeur et semi-mineur : K, Quu et Qvv.
Utilisez les formules suivantes :
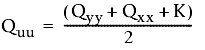
et
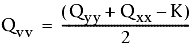
où
- Qxx, Qyy, et Qxy correspondent aux valeurs obtenues à l'aide de la matrice de covariance.
Ces valeurs sont ensuite utilisées pour résoudre deux équations afin de déterminer Su, la longueur de l'axe semi-majeur et Sv, la longueur de l'axe semi-mineur :
et
où
- So = écart type du poids unitaire
Enfin, l'angle t au niveau de l'intersection des axes u et Y est calculé à l'aide de l'équation suivante :
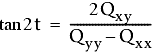
Le point ajusté se trouve vraisemblablement dans l'ellipse (probabilité de 95 ou 99 %).