Nel settore dell'edilizia civile vengono utilizzate varie curve di transizione al fine di introdurre gradualmente la curvatura e la sopraelevazione tra tangenti e curve circolari nonché tra due curve circolari con curvatura diversa.
In relazione con altre tangenti e curve, ogni transizione è in ingresso o in uscita curva.
I due parametri utilizzati più comunemente dagli ingegneri nella progettazione e nell'impostazione di transizioni sono L (lunghezza transizione) ed R (raggio della curva circolare).
Nella seguente figura sono illustrati i diversi parametri di una transizione:
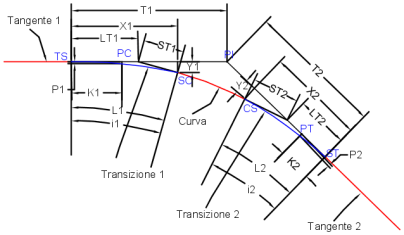
| Parametro transizione | Descrizione |
| i1 | Angolo centrale della curva di transizione L1, ovvero angolo della transizione. |
| i2 | Angolo centrale della curva di transizione L2, ovvero angolo della transizione. |
| T1 | Distanza tangente totale dal vertice planimetrico al punto di tangenza. |
| T2 | Distanza tangente totale dal vertice planimetrico al punto notevole transizione-rettifilo. |
| X1 | Distanza tangente nel punto notevole transizione-curva dal punto di tangenza. |
| X2 | Distanza tangente nella curva-transizione dal punto notevole transizione-rettifilo. |
| Y1 | Distanza di scostamento tangente nel punto notevole transizione-curva dal punto di tangenza. |
| Y2 | Distanza di scostamento tangente nella curva-transizione dal punto notevole transizione-rettifilo. |
| P1 | Scostamento della tangente iniziale in ingresso nel punto di curvatura della curva spostata. |
| P2 | Scostamento della tangente iniziale in uscita dal punto di tangenza della curva spostata. |
| K1 | Ascissa del punto di curvatura spostato rispetto al punto di tangenza. |
| K2 | Ascissa del punto di tangenza spostato rispetto al punto notevole transizione-rettifilo. |
| LT1 | Transizione tangente lunga in ingresso. |
| LT2 | Transizione tangente lunga in uscita. |
| ST1 | Transizione tangente corta in ingresso. |
| ST2 | Transizione tangente corta in uscita. |
| Altri parametri di transizione | |
| A1 | Il valore A equivale alla radice quadrata della lunghezza transizione moltiplicata per il raggio. Misura della planarità della transizione. |
| A2 | Il valore A equivale alla radice quadrata della lunghezza transizione moltiplicata per il raggio. Misura della planarità della transizione. |
Formula
Transizione di continuità
Le transizioni di continuità forniscono una transizione tra due curve circolari con raggi diversi. Come avviene con le transizioni semplici, ciò garantisce la continuità della funzione di curvatura e consente di introdurre una transizione uniforme nella sopraelevazione.
Clotoide
Anche se in AutoCAD Civil 3D sono supportati diversi tipi di transizione, la clotoide è il tipo di uso più frequente. La clotoide viene utilizzata in tutto il mondo sia per progetti di linee ferroviarie che di autostrade.
Presa in esame per la prima volta dal matematico svizzero Leonardo Eulero, la funzione di curvatura della clotoide è una funzione lineare scelta in modo che la curvatura sia uguale a zero (0) come funzione della lunghezza nel punto in cui la transizione incontra la tangente. La curvatura tende poi a diminuire in modo lineare fino ad eguagliare la curva adiacente nel punto di incontro tra la transizione e la curva.
Questo tipo di tracciato garantisce la continuità della funzione di posizione e del relativo primo derivato (azimut locale), analogamente a quanto avverrebbe con una tangente e una curva in un punto di curvatura. Tuttavia, a differenza di una curva semplice, mantiene anche la continuità del secondo derivato (curvatura locale), che diventa sempre più importante mano a mano che aumenta la velocità.
Formula
Le clotoidi possono essere espresse come indicato di seguito: 
Planarità della transizione: 
Angolo totale sotteso dalla transizione: 
La distanza tangente nel punto notevole transizione-curva dal punto tangente-transizione è:
La distanza di scostamento tangente nel punto notevole transizione-curva dal punto tangente-transizione è:
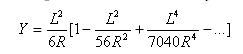
Transizione di Bloss
Anziché utilizzare la clotoide, è possibile utilizzare la transizione di Bloss con la parabola di quinto grado, che rispetto alla clotoide offre il vantaggio di un punto di spostamento minore e, di conseguenza, di una transizione più lunga con un'estensione di transizione maggiore (K). Questo fattore è importante nella progettazione di binari.
Formula
Le transizioni di Bloss possono essere espresse come indicato di seguito.
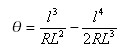
Altre espressioni chiave:
La distanza tangente nel punto notevole transizione-curva dal punto tangente-transizione è:
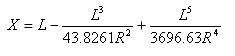
La distanza di scostamento tangente nel punto notevole transizione-curva dal punto tangente-transizione è:
Curve sinusoidali
Queste curve rappresentano un corso di curvatura uniforme e sono applicabili alla transizione tra 0 e 90 gradi delle deflessioni della tangente. Ciononostante le curve sinusoidali non vengono molto utilizzate in quanto hanno un'inclinazione più forte rispetto ad una transizione reale e sono pertanto difficili da estrudere e tracciare.
Formula
Le curve sinusoidali possono essere espresse in vari modi.
Differenziando con l si ottiene un salto di progressiva per l/r, dove r è il raggio di curvatura in un determinato punto:
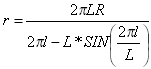
Curva tangente onda semi-sinusoidale in riduzione
Questo tipo di equazione, comunemente utilizzato per la progettazione ferroviaria in Giappone, risulta utile in situazioni in cui è necessaria una transizione efficace nel cambio di curvatura per gli angoli di deflessione bassi (rispetto alla dinamica del veicolo).
Formula
Le curve tangente onda semi-sinusoidale in riduzione possono essere espresse come indicato di seguito.
dove 
e x rappresenta la distanza dall'inizio ad un punto qualsiasi sulla curva e viene misurata lungo la tangente iniziale (estesa); X indica il valore totale di X alla fine della curva di transizione.
Altre espressioni chiave:
La distanza tangente nel punto notevole transizione-curva dal punto tangente-transizione è:
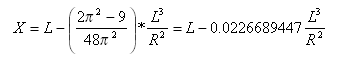
La distanza di scostamento tangente nel punto notevole transizione-curva dal punto tangente-transizione è:
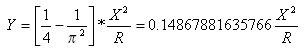
Parabola cubica (Giappone)
Questa transizione è stata sviluppata per soddisfare i requisiti di progettazione giapponesi. Sono state sviluppate alcune approssimazioni della clotoide da utilizzare in situazioni in cui è necessario adattare un angolo di deflessione ridotto o un raggio lungo. Una di tali approssimazioni, utilizzata per la progettazione in Giappone, è la parabola cubica.
Formula
Le parabole cubiche possono essere espresse come indicato di seguito:
Dove X è uguale alla distanza tangente nel punto notevole transizione-curva dal punto tangente-transizione
Oppure come segue:
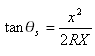
Dove 
è l'angolo centrale della transizione (rappresentato come i1 e i2 nella figura)
Altre espressioni chiave:
La distanza tangente nel punto notevole transizione-curva dal punto tangente-transizione è:
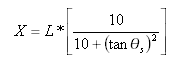
La distanza di scostamento tangente nel punto notevole transizione-curva dal punto tangente-transizione è:
Parabole cubiche
Le parabole cubiche convergono meno rapidamente delle transizioni cubiche e rappresentano quindi la scelta più frequente nella progettazione di ferrovie e autostrade. Sebbene siano meno precise delle transizioni cubiche, le parabole cubiche sono preferite dagli ingegneri stradali e ferroviari in quanto sono espresse in coordinate cartesiane ed è facile impostarle direttamente sul campo.
Formula
Quando -> zero -> si presuppone che cos = l, quindi x = l.
Inoltre, si presuppone che sin = , quindi
x = l e TotalX = (circa) L
La sostituzione di questa approssimazione consente di ottenere il salto di progressiva seguente:
Tutti gli altri parametri corrispondono a quelli della clotoide.
Raggio minimo della parabola cubica
Il raggio in qualsiasi punto su una parabola cubica è:
Una parabola cubica ottiene il r minimo in corrispondenza di:
Pertanto 
Il raggio di una parabola cubica diminuisce da infinito a a 24 gradi, 5 minuti, 41 secondi e a partire da quel momento in avanti inizia ad aumentare nuovamente. Per questo motivo le parabole cubiche si rivelano inutili per deflessioni maggiori di 24 gradi.
Transizioni biquadratiche (Schramm)
Le transizioni biquadratiche (Schramm) presentano valori bassi dell'accelerazione verticale. Esse contengono due parabole di secondo grado i cui raggi variano come funzione della lunghezza della curva.
Formula della curva semplice
Curvatura della prima parabola:
per 
Curvatura della seconda parabola:
per 
Questa curva è specificata dalla lunghezza definita dall'utente (L) della curva di transizione.
Formule della curva di continuità
Curvatura della prima parabola:
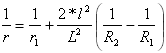per 
Curvatura della seconda parabola:
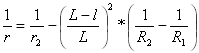per 