Применение итерационного метода, рекомендуется для решения крупномасштабных (15000 - 1 000 000 уравнений) линейных статических задач и проблем собственных значений (модального расчет или расчета устойчивости). Традиционные направления методов (фронтальный, горизонтальный, разряженный) занимают очень много времени и требуют большого объема дискового пространства, для сохранения разложенной матрицы. Такая концепция может быть очень эффективной для расчета конструкций содержащих тела КЭ. Решатели данного типа могут быть очень полезными для линейного статического анализа (например, поиска оптимального параметра конструкции), когда возможно получить близко находящиеся решения для небольшого количества вариантов нагрузок. Элемент за элементом контролирует верность данных Vinget регуляризации (как показано ниже). Назначается дополнительное приложение итеративного решателя, который позволяет обнаружить сложные для поиска ошибки в модели КЭ.
Метод предварительной обработки отклонения (PCG), включающий несколько типов предварительной обработки, в данный момент не реализован.
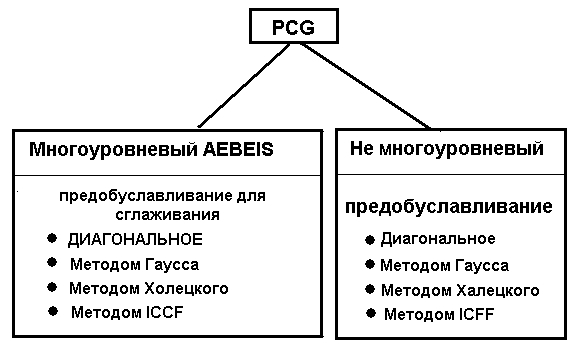
- AEBEIS: объединение элемент за элементом итерационного решателя 1,2;
- EBE: Элемент за элементом;
- ICCF: техника неполной факторизации Холецкого;
AEBEIS – это итерационный метод многоуровневого, накопительного, элемента за элементом интерактивного решателя, который сочетает в себе преимущества быстрых итерационных методов с недорогой техникой EBE. Это позволяет ускорить основные операции с помощью недорогого метода с учетом требований к ресурсам памяти. Объединение таких методов как этот позволяет рассчитывать твердые тела и оболочки, так же хорошо как стержни и сочетания конструкций из балок, оболочек и твердых тел.
AEBEIS, по сравнению с не многоуровневыми методами, обычно обеспечивает схождение быстрее. Он ограничивается только трехмерными конструкциями и двухмерными рамами. В AEBEIS показана сниженная чувствительность к не проработанным проблемам, соответствующим не многоуровневым итеративным методам, но это менее безопасно. В редких случаях "блокирование" симметричной обусловленности выполняется, тогда как сходимость по-прежнему выполняется медленно.
AEBEIS дает возможность применять двухмерные и трехмерные стержневые элементы, оболочки (3, 4, 6, или 8 узловых элементов), твердотельных элементов. Он также включает дополнительные элементы конструкции , такие как упругие опоры, смещения, выпуски и жесткие связи. Не существует ограничений, относящиеся к элементам или типы конструкции для не многоуровневого метода.
Следующие типы симметричной обусловленности доступны AEBEIS и не многоуровневым способов.
- Диагональ - Якоби симметричная обусловленность (применяется только при хорошо обусловленных неполадках).
- EBE Гаусс - симметричная обусловленность Холецкого-Гаусса-Сейделя 1,2 ;
- EBE Холецкого - EBE симметричная обусловленность Холецкого 1,4 ;
- ICCF - техника неполной факторизации Холецкого.5,6 .
ICCF техника быстрее, чем другие методы (Диагональ, EBE Гаусса, EBE Холецкого) и использует примерно одинаковое количество итераций для получения сходимость, таких как методы EBE Гаусса или EBE Холецкого. Она не использует операциям ввода/вывода на жестком диске, но сохраняет в оперативной памяти. Метод ICCF является предпочтительным, если компьютер имеет достаточный объем оперативной памяти. ОЗУ и требования к диску для EBE Гаусса и EBE Холецкого сведены к минимуму, но не такое быстродействие как ICCF.
Ссылки
- Fialko S.Yu. Высокопроизводительное объединение элемент за элементом итеративного решателя для больших объемов сложной конструкции. Архивы гражданского строительства, XLV, 2 1999 г. P.193-207.
- Fialko S., Высокопроизводительное объединение элемент за элементом Ritz-gradient метод конструкции динамического анализа, CAMES, 7: 537-550, 2000.
- Hughes T.J.R., Ferencz м. Неявные решение от крупномасштабных контактов и влияния проблем, предусловие в которых EBE итеративный решатель, IMPACT 87 Int. . Conference on Effects of Fast Transient Loading in the Context of Structural Mechanics, Lausanne, Switzerland, August 26-27, 1987.
- Hughes T.J.R., R.M.Ferencz, and j.O.Hallquist. Large-scale vectorized implicit calculations in solid mechanics on a CRAY X-MP/48 utilizing EBE preconditioned conjugate gradients, Comput. Meths. Appl. Mech. Engrg., 61.
- S.Bitzarakis, M.Papadrakakis, A.Kotsopulos. Параллельные методы решений вычисления механики несущих конструкций. Comp. Methods Appl. Mech. Engrg. 1997, 148 , p.75-104.
- M.Papadrakakis, Solving large - scale problems in mechanics, John Wiley & Sons Ltd., 1993.
См. также:
Параметры итерационного решателя
Выбор параметров итерационных методов решения. Практические рекомендации