При нажатии на кнопку Параметры, расположенную в диалоговом окне Рабочие настройки, на экране появляется диалоговое окно отображенное на риснуке ниже.
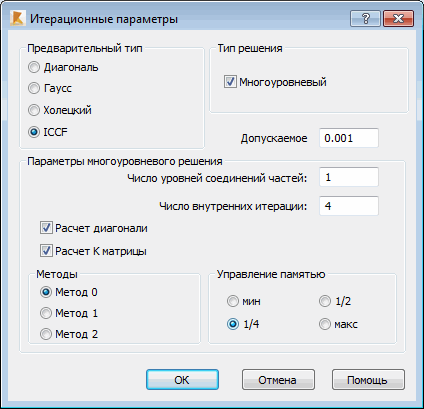
Методы итерации используются при решении длинных уравнений, когда методы перестановки для линейных методов решения неэффективны, а матрица жесткости K достачно хорошо обусловлена. Методы итерации очень эффективны для конечноэлементных моделей (состоящих из сплошных конечных элементов). Для хорошо обусловленных крупномасштабных задач итерационные методы все еще являются очень эффективными инструментами расчета, потому что время линейного расчета очень увеличивается с возрастанием размера задачи. Использование итерационных методов обычно позволяет сократить время расчета и условия хранения на диске. Хотя необходимо принимать во внимание некоторые их недостатки:
- они медленно сходятся при плохо обусловленной задаче;
- каждый вариант нагружения рассчитывется поэтапно – практически сначала; поэтому пользователь должен определить как можно меньше вариантов нагружения.
Для линейного статического расчета и расчете на изгиб и модальном расчете конструкции предлагаются следующие итерационные методы:
Элемент за элементом (PCGEBE), и многоуровневый итерационный метод (AEBEIS)
Метод PCGEBE используется для всех типов конечных элементов и не ограничивается размером задачи. Но он чувствителен к плохой обусловленности матрицы жесткости K – возможна медленная сходимость.
Метод AEBEIS характеризуется быстрой сходимостью для большинства задач. Он также обеспечивает более стабильную сходимость для плохо обусловленных задач. Можно применять 2D и 3D стержневые элементы, все элементы плоских плит и оболочек (3, 4, 6, 8 – узловые элементы), все типы элементов твердых тел, а также все типы элементов дополнительных компонентов конструкции, таких как упругие опоры, жесткие вставки, снятия связей и жесткие узлы. Этот метод осуществляется комбинированием сочетаний методов основанных на технике ЕВЕ.
Тип метода решения
Имеются два типа методов:
- Многоуровневость отключена: PCGEBE.
- Многоуровневость включена: AEBEIS (рекомендуется).
После этого необходимо выбрать тип предварительной обработки данных.
Типы предварительной обработки данных
Методы PCGEBE и AEBEIS основаны на технике EBE. Для них доступны следующие типы предварительной обработкой данных:
- Диагональный - метод Якоби;
- Холецкого - техника EBE Холецкого симметричная предварительная обработка данных;
- Гаусса - техника EBE Холецкого-Гаусса-Зейделя симметричная предварительная обработка данных;
- Данное диалоICCF – техника неполной факторизации Холецкого.
Допуск
Последовательные итерации проводятся до тех пор, пока не выполняется следующее условие:
|| rk || / || b || ≤ tol
rk= b - K xk
максимальный из евклидова и нормального равномерного принимается как нормальный вектор. Нпример:
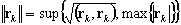
rk – остаточный вектор,
b - правосторонний (вектор нагрузки),
xk – аппроксимированное решение в k-ом итерационном шаге. Этот параметр определяет точность итераций. Если предположить, что tol=0.001, то это означает, что, по крайней мере, первые три цифры величины реакции будут такими же, как в точном решении, полученном с помощью точного решателя (фронтального метода или метода горизонта). Рекомендуется принимать tol=0.001 для предварительного решения (например, при поиске оптимальных расчетных параметров) и tol = {1.0e-04 – 1.0e-08} для окончательного решения.
Расчет матрицы K
Если опция Расчет матрицы K включена, то соответствующие матрицы конечных элементов Ke (e € 1, Nele), где Nele – это номер конечных элементов в рассчитываемой конструкции, рассчитываются каждый раз, когда программа рассчитывает произведение матрицы, умноженной на вектор Kv.
Если опция Расчет K матрицы выключена, то соответствующие матрицы конечных элементов Ke (e € 1, Nele) берутся с диска.
Опция Расчет матрицы К игнорируется для ICCF, но работает для остальных методов предварительного анализа данных:
- Диагональный;
- EBE Гаусс;
- EBE Холецкого;
Многоуровневые параметры решателя
Определение числа уровней накопления; Значение по умолчанию (т.е. 1.0) гарантирует минимальное количество итераций. Этот сложный расчет требует больше места на диске и увеличения времени расчета.
Рекомендуется принимать следующее:
| Количество уравнений. | Количество уровней накопления. |
|---|---|
| < 20 000 | 1 |
| 20 000 - 50 000 | 2 |
| 50 - 200 000 | 3-4 |
| > 200 000 | 4-5 |
Небольшой размер задачи на самой крупном уровне (SPCL) обеспечивает быстрые итерации. Хотя, чем меньше SPCL, тем больше количество итераций.
Число внутренних итераций определяет количество внутренних итераций, выполняемых во время процесса сглаживания. Величина параметра обычно равна 3-4. В некоторых случаях, обычно при расчете больших задач, может оказаться необходимым увеличение количества внутренних итераций (до 8).
Расчет диагонали – выключение этой опции приводит к улучшению накоплений при расчете диагонали матрицы жесткости K. Рекомендуется включать эту опцию, так как улучшенная модель накопления обычно приводит к ускорению сходимости.
Методы
Для методов Диагональ, EBE Гаусса и EBE Холецкого рекомендуется использование любого метода, а для применении подхода ICCF по умолчанию только Метод О.
Метод 0 – это двухуровневый метод, который метод характеризуется самыми быстрыми итерациями. Скорость достижения сходимости самая медленная относительно количества итераций.
Метод 1 – это многоуровневый метод с ограниченными возможностями сглаживания. Такой подход обеспечивает менее интенсивное использование памяти. Это альтернатива для случаев, когда метод 2 невозможно использовать из-за ограниченных возможностей программного обеспечения.
Метод 2 - это многоуровневый метод с использованием сглаживания на каждом уровне накопления. Он обычно характеризуется лучшей сходимостью и позволяет поддерживать максимальное количество уровней накопления. Требования, предъявляемые к месту на диске, в этом случае самые небольшие. Рекомендуется использовать его тогда, когда количество уровней накопления больше двух.
Управление памятью
Определение размера буфера памяти, используемого для хранения матриц элементов и обусловленности. Эта опция работает для следующих типов обусловливания: Диагональ, EBE Гаусса и EBE Холецкого. При подходе ICCF ею пренебрегают. При подходе ICCF ею пренебрегают.
мин - обеспечивает минимальный размер буффера, но она может уменьшить скорость вычислений.
1/4: четверть системной памяти используется для расчетов.
1/2: половина системной памяти используется для расчетов.
макс- максимум системной памяти, предназначенной для расчетов.
Устранение неисправностей
Для уменьшения времени, неоходимого для расчета:
- сократить количество уровней накопления;
- увеличить количество внутренних итераций;
- включить опцию Расчет диагонали;
- использовать Метод 2 или Метод 1, если выбран многоуровневый подход;
В некоторых случаях существует возможность "закрытия" обусловленности для многоуровневого метода. Это приводит к медленной сходимости. Если количество итераций превышает граничное значение bv=40*lg(tol), а желаемый допуск не достигнут, это указывает на медленную сходимость для многоуровневого метода. (Этот критерий не верен для не многоуровневых методов.) В таких случаях рекомендуется выполнить следующие операции:
- увеличить количество внутренних итераций до 8;
- сократить количество уровней накопления, если это не приводит к превышению верхней предельной величины для самого крупного уровня;
- выбрать ICCF или другой не многоуровневый метод (например, так как он быстрее).
Практические рекомендации
Пользователь имеет возможность проверить корректность для кождогоэлемента КЭ матрицы в модели Такая проверка не отнимает много времени при решении больших задач, и мы настойчиво рекомендуем проводить такую проверку один раз перед пробным расчетом конечноэлементной модели.
- открыть диалоговое окно Рабочие настройки;
- перейти на закладку Расчет конструкции;
- выбрать опцию Итерационный;
- нажать кнопку Настройки;
- выключить опцию Многоуровневый;
- выбирать одну из опций ЕВЕ: Гаусс или Холецкий;
- дважды нажать ОК.
- Запускают расчет конструкции.
Если расчетный процесс достигает первой итерации , это означает, что он происходит правильно, и расчет может быть прерван.
Если проверка неправильная, то ошибка 3016 появится при подготовке обусловленности EBE, и расчеты будут прерваны до начала процесса итерации.
См. также:
Параметры итерационного метода. Общая информация.
Решатели, доступные в программе Robot
Выбор параметров итерационных методов решения. Практические рекомендации