Куб

Диалоговое окно Куб в Robot можно открыть двумя способами:

• при выборе команды меню Геометрия > Объекты > Куб;
• Щелкните значок .

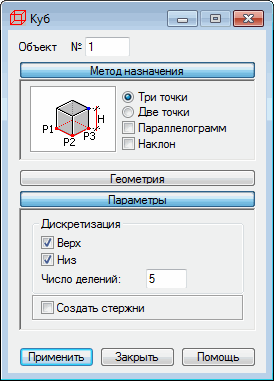
Диалоговое окно разделено на четыре части:

• поле редактирования Объект, в котором вводится номер созданного или выбранного объекта;
• метод назначения;
• Геометрия
• Параметры.

Если диалоговое окно Куб полностью открыто, при нажатии на одну из трех кнопок (Метод назначения, Геометрия или Параметры) минимизируется соответствующая часть окна. Таким образом, диалоговое окно содержит только те опции, которые необходимы пользователю в данный момент. Если диалоговое окно минимизировано, то нажатие на одну из упомянутых выше кнопок приводит к расширению диалогового окна

Метод определения

Опции, позволяющие выбрать метод определения окружности, располагаются в части диалогового окна под названием Метод назначения. Метод зависит от выбора соответствующей опции. Ниже описываются методы определения куба.

Определение куба состоит из двух этапов.

1. Определение четырехугольника – основания куба

   Опция Метод назначения прямоугольника (параллелограмма) доступна в диалоговом окне Методы назначения.

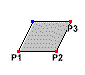
   	Рисунки показывают в общих чертах методы определения прямоугольника.
   	Прямоугольник определяется заданием двух противоположных вершин.

   В этой части диалогового окна доступна опция Параллелограмм. Если в этой опции включен флаг, то определяемый объект будет параллелограммом (углы в создаваемом четырехугольнике не являются прямыми). Если эта опция не активна, создаваемый объект будет прямоугольником.

   Прим.: Параллелограмм определяется, если выбрана опция Три точки.
2. Выбор типа куба

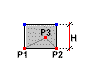
   	Прямой куб В части диалогового окна Геометрия доступно дополнительное окно Высота (высота куба).
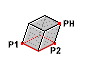
   	Наклонный куб В части диалогового окна Геометрия доступно дополнительное окно Точка РH (точка, определяющая позицию вершины куба).

   Прим.: Диаграммы изменяются в зависимости от выбираемого метода определения куба. Но правила определения куба не изменяются.

Геометрия

Поля в диалоговом окне Геометрия позволяют задавать координаты специфических точек куба. Количество точек зависит от выбираемого метода создания основания куба и типа куба. Имеются дополнительные кнопки для выбора плоскости основания куба. Для выбора плоскости XY, XZ или YZ, на которой должно располагаться основание куба, щелкают соответственно на XY, XZ или YZ. Эти кнопки не доступны, если основание куба – параллелограмм.

Прим.: Если для определения прямоугольника, являющегося основанием куба, выбрана опция Три точки и выбран тип куба "прямой", то возможно определение куба одним из двух способов:

1. заданием координат выбранных вершин куба (графически или введением значений координат в соответствующее поле редактирования) или
2. заданием первой вершины прямоугольника, являющегося основанием куба, путем ввода в поле Точка P1 значений координат первой вершины или графически точкой на экране, вводом длин сторон прямоугольника в поля Точка 2, Точка 3 и высоты куба в поле Высота.

Параметры

В части диалогового окна Параметры имеется поле Дискретизация.

• Верх - Если эта опция активна, то создается верхняя грань цилиндра.
• Низ - Если эта опция активна, то создается определяющий куб объект в виде грани (основания).
• Тело - Опция активизируется, если куб создается как пространственный объект. Опция доступна для объемных конструкций.
• Создать стержни - Если эта опция активна, включен флаг, тогда определяемый куб будет состоять из стержневых элементов (отдельные части куба будут стержнями). Когда опция неактивна, куб генерируется как двумерный объект (плита, оболочка) или трехмерный объект (сплошное твердое тело).

Чтобы определить куб, необходимо:

1. выбрать метод определения куба (основания куба);
2. определить тип куба (прямой, наклонный);
3. задать координаты характерных точек прямоугольника, являющегося основанием куба, и точек, определяющих геометрию куба, одним из способов:
   • текстовое определение: ввод координат отдельных точек в диалоговом окне (часть диалогового окна Геометрия) и нажать на кнопку Применить;
   • в графической форме: щелкнув левой кнопкой мыши в поле P1, расположенном в части диалогового окна Геометрия, включить графический экран и щелкнуть левой кнопкой мыши по точке, представляющей первую точку куба, затем щелкнуть по следующим точкам;
   • использование метода, объединяющего первые два;
4. определить параметры дискретизации куба (число делений в соответствующем направлении).