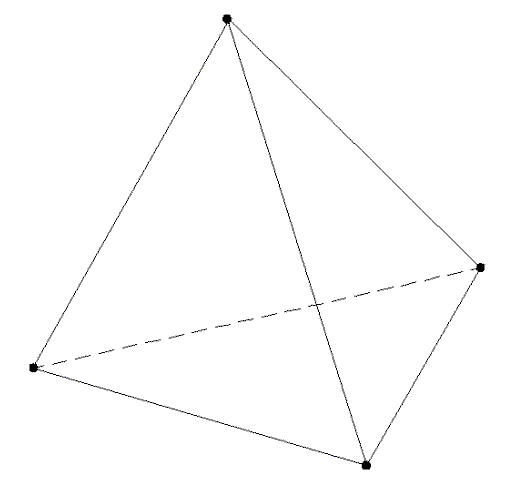
Tetraederelemente sind isoparametrische oder subparametrische gekrümmte Tetraeder mit 4 oder 10 Knoten. Abbildung 1 zeigt einige typische Elemente. Abbildung 2 zeigt ein Beispiel eines Tetraederelements.
Abbildung 1: Typisches Tetraederelement
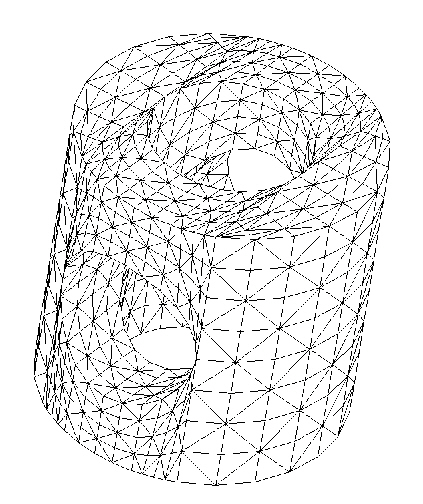
Abbildung 2: Typische Anwendung für ein Tetraederelement
Bestimmung der Flächennummer für Tetraederelemente
Beachten Sie beim Anwenden von Lasten auf eine Flächennummer eines Tetraederbauteils, dass einige Modelle nicht alle Linien auf der Fläche zum Laden auf der gleichen Flächennummer haben. Was geschieht in dieser Situation? Wenn das Modell aus einem CAD-Volumenkörpermodell stammt, erhalten alle Flächen, die mit der Oberfläche des CAD-Modells übereinstimmen, die Last, unabhängig von der Flächennummer der Linien. In manuell erstellten Modellen und auf CAD-Bauteilen, die so geändert wurden, dass das Bauteil nicht mehr mit dem CAD-Bauteil verknüpft ist, definiert die Flächennummer, die zwei der drei Linien einer Flächendefinition gemeinsam haben, die Flächennummer dieser Fläche.
Tetraederelementparameter
Geben Sie zuerst das Materialmodell für dieses Bauteil im Listenfeld Materialmodell des Dialogfeldes Elementdefinition an. Die verfügbaren Materialmodelle sind in folgende Kategorien unterteilt. Einzelheiten zu jedem Materialmodell finden Sie auf der entsprechenden Seite der Seite Materialeigenschaften.
-
Elastisch
- Isotrop: Diese Materialmodelloption wird für Bauteile verwendet, die nur Verformungen im elastischen Bereich der Spannungs-Dehnungs-Kurve aufweisen. Um dieses Materialmodell verwenden zu können, müssen die Bauteile identische Materialeigenschaften in alle Richtungen haben. Die erforderlichen Materialeigenschaften sind ein einzelnes Elastizitätsmodul und Poisson-Koeffizient.
- Orthotrop: Dieses Materialmodell wird für Bauteile verwendet, die nur Verformungen im elastischen Bereich der Spannungs-Dehnungs-Kurve aufweisen. Das Bauteil kann über verschiedene Materialeigenschaften in bestimmte Richtungen verfügen. Die Materialeigenschaften können in einer oder in mehreren der drei orthogonalen Richtungen in einem rechteckigen Koordinatensystem unterschiedlich sein.
- Kurve: Diese Materialmodelloption wird ebenfalls für die Analyse von geologischen Materialien verwendet. In diesem Modell werden die momentanen Kompressions- und Schermodule durch stückweise lineare Funktionen der aktuellen Volumendehnung definiert.
- Temperaturabhängig-isotrop: Dieses Materialmodell wird zur Modellierung von Materialien verwendet, die nur Verformungen im elastischen Bereich der Spannungs-Dehnungs-Kurve haben, aber auch Spannungen aufgrund eines Temperaturunterschieds aufweisen können.
- Temperaturabhängig-orthotrop: Dieses Materialmodell wird für Bauteile mit unterschiedlichen Materialeigenschaften in bestimmten Richtungen verwendet, die sich zudem mit der Temperatur ändern. Die Materialeigenschaften können in einer oder in mehreren der drei orthogonalen Richtungen in einem rechteckigen Koordinatensystem unterschiedlich sein. Die Materialeigenschaften werden bei mehreren Temperaturen angegeben. Die Werte werden zwischen Temperaturwerten linear interpoliert. Der Temperaturbereich, für den die Materialeigenschaften festgelegt sind, muss die erwarteten Temperaturen enthalten.
- Duncan-Chang Erde: Das Duncan-Chang-Modell (1970) dient zum Simulieren von Erde. Es basiert auf triaxialen Bodentests und geht von einem hyperbolischen Spannungs-Dehnungs-Verhältnis aus. Bei Verwendung dieses Materialmodells ist die Analyseerarbeitung auf der Registerkarte Erweitert auf Nur nicht-lineares Material festgelegt.
- Moldflow: Wenn das Bauteil mit dem Spritzgussprozess erstellt wurde, können die anisotropen Materialeigenschaften aus dem Spritzgussprozess einer Autodesk Moldflow-Simulation abgerufen werden. Wählen Sie Moldflow als Materialmodell. Weitere Informationen finden Sie unter Interoperabilität mit Autodesk® Moldflow®.
-
Hyperelastisch
Tipp: Ein höherer Integrationsgrad (auf der Registerkarte Erweitert) für hyperelastische und Schaummaterialien kann die Konvergenz unterstützen, wenn das Bauteil großen Verformungen durchläuft.
- Mooney-Rivlin: Dieses Materialmodell wird zur Modellierung von hyperelastischen Materialien wie Gummi verwendet.
- Arruda-Boyce: Dieses Materialmodell ist ein hyperelastisches Materialmodell zur Modellierung von Gummimaterialien. Die Implementierung folgt dem Materialverhalten nach Ogden für volumenerhaltende Verformungsmodi.
- Ogden: Dieses Materialmodell wird zur Modellierung von hyperelastischen Materialien wie Gummi verwendet.
- Yeoh: Dieses Materialmodell wird zur Modellierung nahezu inkompressibler (volumenerhaltender), hyperelastischer Materialien, z. B. Gummi, verwendet. Hier ist nur die Analysebeschreibung Lagrange gesamt verfügbar.
- Neo-Hookean: Dieses Materialmodell wird zur Modellierung nahezu inkompressibler (volumenerhaltender), hyperelastischer Materialien, z. B. Gummi, verwendet. Hier ist nur die Analysebeschreibung Lagrange gesamt verfügbar.
- Van der Waals: Dieses Materialmodell wird zur Modellierung nahezu inkompressibler (volumenerhaltender), hyperelastischer Materialien, z. B. Gummi, verwendet. Hier ist nur die Analysebeschreibung Lagrange gesamt verfügbar.
-
Schaum
- Blatz-Ko: Dieses Materialmodell umfasst eine starke Kopplung zwischen volumetrischen und nichtvolumetrischen Bauteilen, wie z. B. das Kompressionsmodul. Eine separate Bestimmung wie bei anderen hyperelastischen Materialmodellen ist nicht möglich.
- Hyperelastisch Hyperfoam (Schaumstoff): Dieses Materialmodell wird für hyperelastische Materialien verwendet, ähnlich dem Ogden-Materialmodell. Dieses Materialmodell berücksichtigt die Komprimierbarkeit des Materials. Dies gilt nicht für Layerdehnungselemente.
-
Viskoelastisch
- Viscoelastic Arruda-Boyce: Eine viskoelastische Variation des Arruda-Boyce (hyperelastischen) Materialmodells.
- Viscoelastic Blatz-Ko: Eine viskoelastische Variation des Blatz-Ko- (Schaumstoff-)Materialmodells.
- Thermisch Kriechen viskoelastisch: Dieses Materialmodell wird zur Modellierung von Materialien verwendet, die Verformungen nur im elastischen Bereich der Spannungs-Dehnungs-Kurve aufweisen, jedoch auch Kriechverhalten zeigen können. Kriechen tritt auf, wenn sich ein Modell mit der Zeit unter einer konstanten Last verformt. Weitere Informationen finden Sie im Absatz über das Definieren thermischer Eigenschaften von Tetraederelementen zum Einrichten des Kriechgesetzes für dieses Materialmodell.
- Viskoelastisch Ogden: Eine viskoelastische Variation des Ogden (hyperelastischen) Materialmodells.
- Viscoelastic Hyperschaum: Eine viskoelastische Variation des Hyperschaum-Materialmodells.
- Linear viskoelastisch isotrop: Dies ist ein viskoelastisches Materialmodell, bei dem das Material Eigenschaften eines elastischen Volumenkörpers und einer viskosen Flüssigkeit aufweist. Die viskoelastischen Eigenschaften basieren auf der Prony-Serie. Die Eigenschaften sind in alle Richtungen gleich (isotrop) und unabhängig von der Temperatur.
- Linear viskoelastisch orthotrop: Dies ist ein viskoelastisches Materialmodell, bei dem das Material Eigenschaften eines elastischen Volumenkörpers und einer viskosen Flüssigkeit aufweist. Die viskoelastischen Eigenschaften basieren auf der Prony-Serie. Die Eigenschaften sind in drei lotrechte Richtungen unterschiedlich (orthotrop) und unabhängig von der Temperatur.
- Linear thermisch viskoelastisch isotrop: Dies ist ein viskoelastisches Materialmodell, bei dem das Material Eigenschaften eines elastischen Volumenkörpers und einer viskosen Flüssigkeit aufweist. Die viskoelastischen Eigenschaften basieren auf der Prony-Serie. Die Eigenschaften sind in alle Richtungen gleich (isotrop) und abhängig von der Temperatur.
- Linear thermisch viskoelastisch orthotrop: Dies ist ein viskoelastisches Materialmodell, bei dem das Material Eigenschaften eines elastischen Volumenkörpers und einer viskosen Flüssigkeit aufweist. Die viskoelastischen Eigenschaften basieren auf der Prony-Serie. Die Eigenschaften sind in drei lotrechten Richtungen unterschiedlich (orthotrop) und von der Temperatur abhängig.
- Viscoelastic Mooney-Rivlin: Eine viskoelastische Variation des Mooney-Rivlin (hyperelastischen) Materialmodells.
- Viskoelastisch Neo-Hookean: Dies ist eine viskoelastische Variation des (hyperelastischen) Materialmodells Neo-Hookean für die finite Verformung.
- Viskoelastisch Yeoh: Dies ist eine viskoelastische Variation des (hyperelastischen) Materialmodells Yeoh für die finite Verformung.
- Viskoelastisch Van der Waals: Dies ist eine viskoelastische Variation des (hyperelastischen) Materialmodells Van der Waals für die finite Verformung.
-
Plastisch
- von Mises mit isotroper Verhärtung: Diese Materialmodelloption wird für Bauteile verwendet, die während der Analyse eine plastische Verformung aufweisen können. Es wird eine bilineare Kurve definiert, um das Spannungs-Dehnungs-Verhältnis zu steuern.
- von Mises mit kinematischer Verhärtung: Diese Materialmodelloption wird ebenfalls für Bauteile verwendet, die während der Analyse eine plastische Verformung aufweisen können. Es wird eine bilineare Kurve definiert, um das Spannungs-Dehnungs-Verhältnis zu steuern. Diese Materialmodelloption ist der Option von Mises mit isotroper Erhärtung vorzuziehen, wenn das Modell einer zyklischen Last ausgesetzt werden soll.
- von Mises-Kurve mit isotroper Verhärtung: Diese Materialmodelloption wird für Bauteile verwendet, die während der Analyse eine plastische Verformung aufweisen können. Sie können eine Spannungs-Dehnungs-Kurve mit mehreren Datenpunkten bestimmen, um das Spannungs-Dehnungs-Verhältnis zu steuern.
- von Mises-Kurve mit kinematischer Verhärtung: Diese Materialmodelloption wird für Bauteile verwendet, die während der Analyse eine plastische Verformung aufweisen können. Sie können eine Spannungs-Dehnungs-Kurve mit mehreren Datenpunkten bestimmen, um das Spannungs-Dehnungs-Verhältnis zu steuern. Diese Materialmodelloption ist der Option von Mises mit isotroper Erhärtung vorzuziehen, wenn das Modell einer zyklischen Last (Bauschinger-Effekt) ausgesetzt werden soll.
- Temperaturabhängige Plastizität: Dieses Materialmodell wird zur Modellierung von Materialien verwendet, die während der Analyse eine plastische Verformung und aufgrund eines Temperaturunterschieds auch Spannung aufweisen können.
-
Viskoplastisch
- Thermisch Kriechen viskoplastisch: Dieses Materialmodell wird zur Modellierung von Materialien verwendet, die eine plastische Verformung und auch Kriechverhalten aufweisen können. Kriechen tritt auf, wenn sich ein Modell mit der Zeit unter eine konstanten Last verformt. Weitere Informationen finden Sie im Absatz über das Definieren thermischer Eigenschaften von Tetraederelementen zum Einrichten des Kriechgesetzes für dieses Materialmodell.
- Drucker-Prager: Dieses Materialmodell ähnelt den von Mises-Materialmodellen, verfügt zusätzlich jedoch noch über eine Fließfunktion. Das Modell geht davon aus, dass die volumetrische Belastung die Fließfunktion ändert. Dies ist in Materialien wie Beton und Felsen der Fall.
-
Beton
- Armierter Beton: Dieses Materialmodell lässt verschiedenes Zug- und Druckverhalten zu. Es kann Rissbildungen und Fehler bei der Zerkleinerung des Betons unter relativ monotoner Last simulieren. Rissbildung und Zerkleinerung werden über die Degeneration der Elastizität an den Integrationspunkten simuliert anstatt einzelne makroskopische Risse zu verfolgen. Maximal drei unabhängige Richtungen der Armierungen sind für das Betonmaterial zulässig. Die Details der Armierungspositionen (Höhe oder Tiefe) werden nicht berücksichtigt. Sie werden im gesamten Bauteil als verwischt angesehen. Bei Verwendung des Materialmodells Armierter Beton wird die Analysebeschreibung auf der Registerkarte Erweitert auf Nur nicht-lineares Material festgelegt.
-
Elektrisch
- Piezoelektrisch: Dieses Materialmodell ist für Bauteile, bei denen Spannung als Ergebnis eines elektrischen Spannungsunterschieds auftritt. Sie müssen sowohl die elastischen als auch die piezoelektrischen Eigenschaften angeben.
- Allgemein Piezoelektrisch: Dieses Materialmodell ist eine allgemeine Form des piezoelektrischen Materialmodells. Sie müssen die elastische Steifigkeit und die piezoelektrischen Matrixkoeffizienten angeben.
Damit für die Tetraederelemente in diesem Bauteil die Mittelknoten aktiviert sind, wählen Sie in der Dropdown-Liste Mittelknoten die Option Einbezogen. Wenn diese Option ausgewählt ist, haben die Tetraederelemente zusätzliche Knoten in der Mitte jeder Kante definiert. (Bei Netzen von CAD-Volumenkörpermodellen folgen mittlere Knoten der ursprünglichen Krümmung der CAD-Oberfläche, abhängig von der gewählten Option, bevor das Netz erstellt wurde. Bei handgefertigten Modellen und geänderten CAD-Modellnetzen befindet sich der mittlere Knoten in der Mitte zwischen Eckknoten.) Dadurch wird ein Tetraederelement mit 4 Knoten in ein Tetraederelement mit 10 Knoten geändert. Ein Element mit Mittelknoten führt zu genauer berechneten Verläufen. Dies ist besonders nützlich, wenn Sie versuchen, das Biegeverhalten mit einigen Elementen auf der Biegeebene zu modellieren. Elemente mit mittleren Knoten verlängern die Verarbeitungszeit. Wenn das Netz ausreichend klein ist, wird mit den Mittelknoten u. U. kein wesentlich genaueres Ergebnis erzielt.
Verwenden Sie die Dropdown-Liste Analyseart, um den erwarteten Verschiebungstyp festzulegen. Kleine Verschiebung eignet sich für Bauteile, bei denen keine Bewegungen und nur kleine Dehnungen auftreten, und ignoriert alle geometrischen Effekte, die sich aus großen Verschiebungen ergeben. (Außerdem wird für Analysebeschreibung auf der Registerkarte Erweitert die Option Nur Material-Nichtlinear festgelegt). Große Verschiebungen eignet sich für Bauteile, die keine Bewegung und/oder große Dehnungen aufweisen. (Die Analysebeschreibung auf der Registerkarte Erweiterte Einstellungen sollte ebenfalls der Analyse entsprechend festgelegt werden.)
- Die Verschiebung an den Mittelknoten ist immer eine Ausgabe. Bei der Spannung und Dehnung an den Mittelknoten handelt es sich nur um Ausgaben, wenn der Benutzer die Option zur Ausgabe dieser Ergebnisse vor der Durchführung der Analyse aktiviert. Die Option befindet sich im Dialogfeld Einrichten
 Modell einrichten
Modell einrichten Parameter
Parameter Erweitert auf der Registerkarte Ausgabe. (Weitere Informationen finden Sie unter Steuern der Ausgabedateien.)
Erweitert auf der Registerkarte Ausgabe. (Weitere Informationen finden Sie unter Steuern der Ausgabedateien.) - Legen Sie auf der Registerkarte

 Optionen
Optionen Analyse die Option Große Verschiebungen als Standard in nichtlinearen Analysen fest, um zu steuern, ob die Analyseart die Vorgabeeinstellungen für kleine oder große Verschiebungen übernimmt.
Analyse die Option Große Verschiebungen als Standard in nichtlinearen Analysen fest, um zu steuern, ob die Analyseart die Vorgabeeinstellungen für kleine oder große Verschiebungen übernimmt.
Definieren der thermischen Eigenschaften von Tetraederelementen
Abschnitt Thermisch:
Wenn ein Tetraederelement-Bauteil ein Materialmodell mit thermischen Effekten verwendet, müssen Sie im Feld Spannungsfreie Referenztemperatur auf der Registerkarte Thermisch des Dialogfelds Elementdefinition einen Wert festlegen. Dieser Wert wird als Referenztemperatur verwendet, um elementbasierte Lasten zu berechnen, die mittels bilinearer Interpolation von Knotentemperaturen einer Abhängigkeit mit thermischem Wachstum zugewiesen wurde.
Abschnitt Kriechdehnung:
Wenn ein Tetraederelement-Bauteil ein Materialmodell mit Kriechdehnung verwendet, wählen Sie die Option in der Dropdown-Liste Kriechgesetz aus. Diese Auswahl wird bei der Analyse zum Berechnen der Kriecheffekte verwendet. Folgende Kriechgesetze stehen zur Verfügung:
- Kein Kriechen: Wenn diese Option ausgewählt wird, werden keine Kriecheffekte in der Analyse berücksichtigt.
- Potenzgesetz: Diese Option ist auch als uniaxiales Kriechgesetz bekannt. Die Gleichung ist
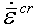 = C
1
x
= C
1
x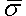 C2
x t
C3
.
C2
x t
C3
. - Garofalo: Diese Option ist auch als hyperbolisches Sinus-Kriechgesetz bekannt. Die Gleichung ist
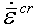 = A
0
x [sinh(A
1
x
= A
0
x [sinh(A
1
x 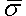 )]
A2
.
)]
A2
. - Doppeltes Potenzgesetz: Diese Option ähnelt dem Potenzgesetz, hat jedoch eine zusätzliche Größe, um Ergebnisse zu erzielen, die bei hohen Spannungswerten näher an experimentellen Ergebnissen liegen. Die Gleichung ist
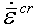 = C
1
x
= C
1
x 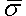 C
2
x t
C3
+ C
4
x
C
2
x t
C3
+ C
4
x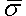 C5
x t
C6
.
C5
x t
C6
.
Dabei ist![]() die effektive Kriechdehnungsrate und
die effektive Kriechdehnungsrate und![]() ist die effektive Spannung. Wichtige Informationen zum Eingeben der Materialeigenschaften finden Sie auch unter Viskoelastische Materialeigenschaften für das thermische Kriechverhalten.
ist die effektive Spannung. Wichtige Informationen zum Eingeben der Materialeigenschaften finden Sie auch unter Viskoelastische Materialeigenschaften für das thermische Kriechverhalten.
Wenn die Kriechanalysen für gleich große Unterteilungen des Zeitschritts berechnet werden sollen, wählen Sie die Option Feste Unterschritte im Dropdown-Feld Zeit-Integrationsmethode. Wenn die Kriechanalysen für unterschiedlich große Unterteilungen des Zeitschritts berechnet werden sollen, wählen Sie die Option Flexible Unterschritte. Diese beiden Methoden basieren auf einer zeitlichen Erhärtung und verwenden explizite Zeit-Integrationsmethoden. Diese Methoden können unter bestimmten Lastbedingungen instabil werden. Wenn Sie das Materialmodell Thermisch Creep viskoelastisch verwenden und das Dropdown-Feld Kriechdehnungsdefinition nicht auf Geändert eingestellt ist, ist im Dropdown-Feld Zeit-Integrationsmethode eine zusätzliche Option verfügbar: die Alpha-Methode. Diese Methode verwendet ein implizites Zeit-Integrationsschema zur Verbesserung des Kriechverhaltens. Diese Methode kann uneingeschränkt stabil sein.
Geben Sie die Temperatur an, bei der keine thermische Spannung im Feld Spannungsfreie Referenztemperatur vorhanden ist.
Wenn Sie eine Analyse mit nicht-zyklischer Belastung ausführen, wählen Sie die Option Effektiv in der Dropdown-Liste Kriechdehnungsdefinition aus. Wenn Sie eine Analyse mit zyklischer Belastung ausführen, verwenden Sie die Option Geändert.
Bei der Analyse werden die Kriechanalysen als Iterationen in Unterschritten jedes Zeitschritts ausgeführt. Sie können im Feld Maximale Anzahl der Teilschritte festlegen, wie viele Unterschritte in einem einzigen Zeitschritt zulässig sind. Im Feld Höchstanzahl der Iterationen in einem Teilschritt können Sie ferner festlegen, wie viele Iterationen in einem einzigen Unterschritt ausgeführt werden können. Nach jeder Unterschritt-Iteration werden Kriechspannung und -dehnung mit der vorherigen Iteration verglichen. Wenn der Wert nicht innerhalb der in den Feldern Kriechdehnungskalkulationstoleranz und Kriechspannungs-Kalkulationstoleranz festgelegten Toleranzen liegt, ist eine andere Iteration erforderlich.
Wenn Sie eine Zeit-Integrationsmethode der Alpha-Methode verwenden, muss der Zeit-Integrationsparameter festgelegt werden. Um für das Zeit-Integrationsschema eine vollständig explizite Methode zu verwenden (aber eine andere als die explizite Methode mit festen/flexiblen Unterschritten), geben Sie in das Feld Zeit-Integrationsparameter den Wert 0.0 ein. Um eine vollständig implizite Methode zu verwenden, geben Sie in das Feld Zeit-Integrationsparameter den Wert 1.0 ein. Wenn der Integrationsparameter größer als 0.5 ist, ist diese Methode uneingeschränkt stabil.
Steuern der Ausrichtung von Tetraederelementen
Wenn in diesem Teil der Tetraederelemente ein orthotropisches Materialmodell verwendet wird, müssen Sie die Ausrichtung der Materialachsen 1, 2 und 3 auf der Registerkarte Orthotrop im Dialogfeld Elementdefinition definieren. Es gibt zwei grundlegende Methoden, um dies zu erreichen.
Methode 1:
Bei der ersten Methode wird eine der globalen Achsen als Materialachse 1 ausgewählt. Wenn Sie die Option Globale X-Richtung im Dropdown-Feld Materialachsenrichtung festgelegt mit auswählen, folgen die orthogonalen Materialachsen den Achsen X, Y und Z wie folgt:
- Materialachse 1: X-Achse
- Materialachse 2: Y-Achse
- Materialachse 3: Z-Achse
Wenn Sie die Option Globale Y-Richtung im Dropdown-Feld Materialachsenrichtung festgelegt mit auswählen, folgen die orthogonalen Materialachsen den Achsen X, Y und Z wie folgt:
- Materialachse 1: Y-Achse
- Materialachse 2: Z-Achse
- Materialachse 3: X-Achse
Wenn Sie die Option Globale Z-Richtung im Dropdown-Feld Materialachsenrichtung festgelegt mit auswählen, folgen die orthogonalen Materialachsen den Achsen X, Y und Z wie folgt:
- Materialachse 1: Z-Achse
- Materialachse 2: X-Achse
- Materialachse 3: Y-Achse
Mit der ersten Methode können die Achsen um die ausgewählte globale Richtung gedreht werden, indem Sie einen Winkel im Feld Materialachsen-Drehungswinkel eingeben. Dieser Winkel folgt der Rechte-Hand-Regel.
Methode 2:
Bei der zweiten Methode wird die Option Räumliche Punkte im Dropdown-Menü Materialachsenausrichtung festgelegt mit ausgewählt. Als Nächstes definieren Sie die Koordinaten für drei räumliche Punkte in der Tabelle Räumliche Punktkoordinaten. Wählen Sie dann den entsprechenden Index für die räumlichen Punkte in den Dropdown-Menüs Index des räumlichen Punkts 1, Index des räumlichen Punkts 2 und Index des räumlichen Punkts 3 aus.
- Materialachse 1 ist ein Vektor vom räumlichen Punkt im Dropdown-Menü Index des räumlichen Punkts 1 zum räumlichen Punkt im Dropdown-Menü Index des räumlichen Punkts 2.
- Materialachse 2 ist senkrecht zur lokalen Achse 1, liegt in der durch die drei räumlichen Punkte gebildeten Ebene und befindet sich auf der gleichen Seite von Achse 1 wie der räumliche Punkt im Dropdown-Menü Index des räumlichen Punkts 3.
- Materialachse 3 wird als Kreuzprodukt der Materialachsen 1 und 2 berechnet.

Abbildung 3: Ausrichtung der Materialachsen
Erweiterte Parameter von Tetraederelementen
Analyseformulierung: Wählen Sie in der Dropdown-Liste Analyseformulierung auf der Registerkarte Erweitert die Formulierungsmethode aus, die Sie für die Tetraederelemente verwenden möchten.
- Wenn die Option Nur Material-Nichtlinear aktiviert ist, werden nichtlineare Materialmodelleffekte berücksichtigt, alle Analysen werden jedoch basierend auf der nicht deformierten Geometrie durchgeführt. Diese Formulierung eignet sich also für Bauteile mit kleinen Dehnungen und keiner Bewegung. Dies ist die einzige verfügbare Option, wenn auf der Registerkarte Allgemein als Analyseart die Option Kleine Verschiebungen ausgewählt wurde.
- Die Option Lagrange gesamt richtet sich nach der ursprünglichen, nicht verschobenen Konfiguration des Modells für alle statischen und kinematischen Variablen. Die Formulierung eignet sich für Bauteile mit Bewegung und kleinen Dehnungen. Beachten Sie, dass die Materialeigenschaften sich auf die Spannung und Dehnung beziehen müssen.
- Die Option Lagrange aktualisiert bezieht sich auf die zuletzt berechnete Konfiguration des Modells für alle statischen und kinematischen Variablen. Die Formulierung eignet sich für Bauteile mit Bewegung und großen Dehnungen. Beachten Sie, dass die Materialeigenschaften sich auf die tatsächliche Spannung und Dehnung beziehen müssen.
Aktualisierungsmethode für Spannung:
Die Aktualisierungsmethode für Spannung wird verwendet, wenn als Materialmodell (auf der Registerkarte Allgemein) eines der folgenden plastischen Materialmodelle festgelegt wird:
- von Mises mit isotroper Erhärtung
- von Mises mit kinematischer Erhärtung
- von Mises Kurve mit isotroper Erhärtung
- von Mises Kurve mit isotroper Erhärtung
Diese Einstellung steuert den numerischen Algorithmus für die Integration der konstitutiven Gleichungen (Spannungs-/Dehnungsgesetz), wenn das Material plastisch wird. Als Aktualisierungsmethode für Spannung stehen die folgenden Optionen zur Verfügung:
- Explizit: (ursprüngliche Methode). Diese Option verwendet das explizite subinkrementelle Forward-Euler-Verfahren zur Integration der konstitutiven Gleichungen. Die Option Explizit eignet sich am besten für einfache Probleme, wie einfache Spannung, da die Methode schneller ausgeführt wird. Diese Option reagiert jedoch empfindlicher auf die Last, Zeitschrittgröße und Komplexität der Spannungs-Dehnungs-Kurve des Materials.
- Allgemeine Mittenpunkt: Diese Option verwendet eine implizite Methode für die Integration der konstitutiven Gleichungen. Sie reduziert die Fehlerhäufung und stellt sicher, dass der Aktualisierungsprozess für die Spannung uneingeschränkt stabil ist. Daher eignet sich diese Option besser für komplizierte Analysen, z. B. Kontaktprobleme und starke Plastizität oder komplexen Spannungs-Dehnungskurven für Material.
Richtlinien für die Aktualisierungsmethode für Spannung:
- Überprüfen Sie, ob die Analyseergebnisse Sinn machen (d. h., ob sie das erwartete Verhalten zeigen). Wenn beispielsweise die Geometrie, Lasten und Randbedingungen Symmetrie aufweisen, sind symmetrische Ergebnisse zu erwarten (mit Ausnahme von anisotropischen Materialien). Wenn die Ergebnisse kontraintuitiv sind oder die Lösung Unterbrechungen oder Instabilität aufweist, ändern Sie die Aktualisierungsmethode für Spannung, oder erhöhen Sie die Aktualisierungsgeschwindigkeit der Variablen, wie in der nächsten Richtlinie beschrieben.
- Unabhängig davon, ob Sie Explizit oder Allgemeine Mittenpunkt wählen, verbessert die häufigere Aktualisierung der Spannungs- und Dehnungsvariablen die Lösung für Kunststoffmaterialmodelle. Verwenden Sie eine der folgenden Methoden, um die Aktualisierungsgeschwindigkeit zu erhöhen:
- Verringern Sie die Zeitschrittgröße (Abtastrate erhöhen) in den Analysenparametern.
- Wählen Sie anstatt Automatisch oder Kombiniertes Newton auf der Registerkarte Gleichgewicht des Dialogfelds Analysenparameter - Erweitert die Option Volles Newton als Nichtlinear-iterative Lösungsmethode.
- Normalerweise lässt die Methode Allgemeiner Mittenpunkt größere Zeitschritte zu als die Methode Explizit und erzielt zudem noch genauere Ergebnisse, sie ist jedoch rechenintensiver.
- Hintergrund: Die Integration der grundlegenden Beziehungen, um unbekannte Spannungsinkremente zu erhalten, ist beim mechanischen Ereignissimulator (MES) entscheidend. Diese Beziehungen definieren eine Reihe gewöhnlicher Differenzialgleichungen. Methoden, um diese zu integrieren, werden in der Regel als explizit oder implizit klassifiziert. Die explizite Methode ist ausschließlich vorausschauend. Das bedeutet, dass die Neigung der Spannungs-Dehnungskurve zu Beginn eines Inkrements gewählt wird. Diese Neigung wird zum Berechnen der Spannung am Ende des Inkrements verwendet. Bei der impliziten Methode ist der Solver voraus- und rückwärtsschauend. Die Neigung muss mit mehreren Iterationen berechnet werden. Das Dehnungsinkrement wird mit der Neigung der Spannungs-Dehnungskurve multipliziert, um die Spannung zu ermitteln.
Beim Integrationsschema Explizit werden Fließfläche, potenzielle Kunststoffverläufe und Verfestigungsgesetz in bekannten Spannungszuständen berechnet. Es sind keine bestimmten Iterationem unbedingt erforderlich, um die endgültigen Spannungen vorherzusehen.
Beim Schema Allgemeiner Mittenpunkt (eine implizite Methode) werden die Spannungen und Verfestigungsparameter des nächsten Inkrements für die Fließfläche mit einer einfachen iterativen Anpassung wiederhergestellt, da diese Bedingung durch die Integration nicht erzwungen wird. Diese Korrektur erfordert einen zusätzlichen Aufwand für das iterative Lösen der nichtlinearen Gleichungen. Umgekehrt gilt, dass explizite Methoden keine Lösung eines Systems nichtlinearer Gleichungen zur Berechnung der Spannungen an jedem Gaußschen Punkt erfordern.
Der Wert für Parameter für allgemeinen Mittenpunkt wird verwendet, wenn für die Aktualisierungsmethode für Spannung die Option Allgemeiner Mittenpunkt ausgewählt wird. Der gültige Bereich für diesen Wert liegt zwischen 0 und 1 (einschließlich). Wenn für den Parameter 0 festgelegt wird, ist der resultierende Algorithmus ein vollständig explizites Mitglied der Algorithmus-Familie (ähnlich der Option Explizit für Aktualisierungsmethode für Spannung); die Lösung ist jedoch nicht uneingeschränkt stabil. Wenn der Parameter 0.5 oder größer ist, ist die Methode uneingeschränkt stabil. Wenn für den Parameter 0.5 festgelegt wurde, ist die Lösung ein Mittelpunkt-Algorithmus; wenn der Wert 1 ist, wird die Lösung als vollständiger Backward-Euler-Algorithmus oder Nächster-Punkt-Algorithmus bezeichnet und ist vollständig implizit. Ein Wert von 1 ist genauer als andere Werte, insbesondere bei großen Zeitschritten.
Dehnungsmessungen:
Die Option Dehnungsmessungen wird verwendet, wenn für das Materialmodell (auf der Registerkarte Allgemein) Isotrop und für die Analysebeschreibung Lagrange aktualisiert festgelegt wird. Die Optionen sollen die Konvergenz der Methode Lagrange aktualisiert verbessern. Für die Dehnungsmessungen sind folgende Optionen verfügbar:
- Almansi Dehnung: (ursprüngliche Methode). Diese Option verwendet die Cauchy-Spannung und die Almansi-Dehnung für die konstitutive Beziehung. Sie ist jedoch auf Fälle mit kleiner Dehnung beschränkt.
- Log-Dehnung: Diese Option verwendet die Cauchy-Spannung und die virtuelle Log-Dehnung (inkrementelle Dehnung) für die konstitutive Beziehung. Sie ist in allen Fällen akzeptabel, auch bei großen Dehnungen. Dies ist ein hypoelastisches Modell und hat den Nachteil, dass es bei nicht komprimierbarem Material (Poisson-Koeffizient = 0.5) besser funktioniert als bei komprimierbaren Materialien. Grund hierfür ist die Annahme, dass das Schermodul eine Konstante ist, während es sich in Wirklichkeit an das sich ändernde Volumen anpasst.
Überlappende Elemente:
Wenn das Kontrollkästchen Überlappen der Elemente zulassen aktiviert ist, wird beim Dekodieren der Linien in Elemente die Erstellung überlappender Elemente zugelassen. Eine Überlappung kann bei der Modellierung von Elementen erforderlich sein. Dies gilt besonders für Probleme, die auf planare Bewegung beschränkt sind.
Ausgabeoptionen:
Aktivieren Sie das Kontrollkästchen Detaillierte Ausgabe von Kräften und Momenten, um die Spannungsergebnisse für jedes Element bei jedem Zeitschritt während der Analyse in die Textprotokolldatei zu schreiben. Dies kann zu großen Ausgabemengen führen.
Wenn eines der von Mises-Materialmodelle ausgewählt wurde, können Sie wählen, ob der aktuelle Materialstatus (elastisch oder plastisch), die aktuelle Streckgrenze, die aktuelle Fließspannungsgrenze, die zugehörige Spannungsgrenze und die entsprechende Ausgabe für plastische Spannung an Eckknoten und/oder Integrationspunkten bei jedem Zeitschritt vorhanden sein sollen. Wählen Sie dazu die entsprechende Option in der Dropdown-Liste Weitere Ausgabe aus.
Selektiv reduzierte Integration (mittlere Dehnung):
Viele physikalische Probleme hängen mit Bewegungen zusammen, die im Wesentlichen das Volumen beibehalten. Materialien, die sich so verhalten, werden als nicht komprimierbar bezeichnet. Beispielsweise sind Gummi und Metalle mit starr-plastischer Strömung nahezu nicht komprimierbar. Durch die Aktivierung des Kontrollkästchens Selektiv reduzierte Integration (mittlere Dehnung) wird eine Änderung zu den üblichen komprimierbaren FEM-Formulierungen hinzugefügt, die die Grenze der Inkompressibilität und die hoch komprimierbare Volumenänderung darstellt. Diese Methode (B-Bar) kann dazu beitragen, dass Volumenblockieren vermieden wird.
Wenn diese Option nicht aktiviert ist, werden die Dehnungskomponenten der Verformungen (volumenbezogen) in der gleichen Reihenfolge mit den deviatorischen Komponenten integriert. Wenn diese Option aktiviert ist, wird der mittlere Wert zur Berechnung des Dehnungsanteils verwendet.
Zwei Beispiele, in denen diese Option Vorteile bei der Analyse bringt:
- Materialeigenschaften: Bei isotroper linearer Elastizität kann die Bedingung der Inkompressibilität als Poisson-Koeffizient ausgedrückt werden. Wenn sich der Poisson-Koeffizient 0.5 nähert, wird der Widerstand gegenüber Volumenänderungen stark erhöht, vorausgesetzt, dass der Scherwiderstand konstant bleibt. Das Kompressionsmodul nähert sich unendlich.
- Materialmodelle und Verformung: Bei elasto-plastischen Materialmodellen ist die plastische Verformung viel größer als die elastische Verformung. In der mechanischen Theorie wird davon ausgegangen, dass bei plastischen Verformungen keine Volumenänderung auftritt. Das Material verfügt somit über ein nahezu konstantes Volumen. Ähnliche Annahmen bestehen auch für andere nichtlineare Materialmodelle.
Um das Kontrollkästchen Selektiv reduzierte Integration (mittlere Dehnung) zu aktivieren, muss für Kompatibilität die Option Erzwungen festgelegt sein.
Piezoelektrische Materialoptionen:
Wenn für ein Bauteil eines der beiden piezoelektrischen Materialmodelle ausgewählt wurde, sind zwei weitere Optionen auf der Registerkarte Erweitert im Dialogfeld Elementdefinition verfügbar.
- Verwenden Sie das Eingabefeld Knotenvolt-Lastkurve, um die Nummer der Lastkurve anzugeben, die zum Steuern aller Knotenvoltwerte bei der Analyse verwendet wird.
- Spannungsdifferenzen, die auf piezoelektrische Materialien angewendet werden, erzeugen ein elektrisches Feld, das zu einer geringfügigen Verformung des piezoelektrischen Bauteils führt. Die Dehnung ist in der Regel nur sehr gering. Die Verformung des Bauteils hat eine geringe Auswirkung auf das elektrische Feld, was wiederum eine geringe Auswirkung auf die resultierende piezoelektrische Verformung hat. Um diesen Effekt zu berücksichtigen, aktivieren Sie das Kontrollkästchen Elektrisches Feld aktualisieren. Andernfalls basiert das elektrische Feld auf dem ursprünglichen (unverschobenen) Zustand des Bauteils.
Definieren von Bodenverhältnissen
Wenn das Materialmodell Duncan-Chang ausgewählt ist, wird die Registerkarte Erdreich aktiviert. Machen Sie entsprechend der Analyse die folgenden Eingaben. Diese Eingabe bezieht sich auf den Anfangszustand des Bodens. Weitere Informationen finden Sie auch auf der Seite Einrichten und Durchführen der Analyse: Nichtlinear: Materialeigenschaften: Duncan-Chang-Materialeigenschaften: Theoretische Beschreibung von Duncan-Chang.
- Hydrostatischen Druck überlagern: Wenn diese Option aktiviert ist, wird die Anfangsspannung aus einem konstanten hydrostatischen Druck erstellt, der in das entsprechende Feld eingegeben wird. (Der hydrostatische Druck wirkt in diesem Fall gleichmäßig in alle Richtungen und ist nicht mit einem Druck zu verwechseln, der mit der Tiefe wächst). Der Wert für den Druck muss größer als 0 sein.
- Eigengewicht überlagern: Wenn diese Option aktiviert ist, wird die Anfangsspannung aus dem Gewicht des modellierten Bodens erstellt.
- Referenzpunkt auf Oberfläche: Geben Sie eine X-, Y- und Z-Koordinate an. Dadurch wird festgelegt, wo der Druck aufgrund des Gewichts der Erde gleich null ist. Wenn das Modell ein Bodenabschnitt tief unter der Erde ist, dann kann der Referenzpunkt über dem modellierten Bauteil liegen.
- Quererddruck-Koeffizient: Die meisten Böden erzeugen keine echte hydrostatische Spannung (gleichmäßig in alle Richtungen). Die Spannung in die horizontale Richtung beträgt normalerweise ein Bruchteil der vertikalen normalen Spannung. Das Verhältnis von lateraler und vertikaler Spannung definiert den Koeffizienten des ebenen Erddrucks. Die Eingabe sollte in einem Bereich zwischen 0 und 1 liegen.
- Gravitationsbeschleunigung: Um aufgrund des Eigengewichts eine Spannungsverteilung zu erzeugen, geben Sie die Gravitationskonstante und die Richtung ein, in die die Schwerkraft wirkt, um die Spannungsverteilung zu erstellen. Die Richtung ist normalerweise die gleiche Richtung, in die die Schwerkraft in der Analyse wirkt. Es kann jedoch auch eine andere Richtung verwendet werden, wenn das Modell den Boden in einer anderen Ausrichtung zwischen dem Zeitpunkt, zu dem die Anfangsspannung erstellt wurde, und der aktuellen Ausrichtung des Modells darstellt. Der Boden wurde verschoben.
Grundlegende Schritte für die Verwendung von Tetraederelementen
- Stellen Sie sicher, dass ein Einheitensystem definiert ist.
- Stellen Sie sicher, dass das Modell einen nichtlinearen Analysetyp verwendet.
- Klicken Sie mit der rechten Maustaste auf die Überschrift Elementtyp für das Bauteil, das als Quaderelement dienen soll.
- Klicken Sie auf den Befehl Tetraeder.
- Klicken Sie mit der rechten Maustaste auf die Überschrift Elementdefinition.
- Wählen Sie den Befehl Elementdefinition bearbeiten.
- Wählen Sie auf der Registerkarte Allgemein das gewünschte Materialmodell im Dropdown-Feld Materialmodell aus.
- Wenn Sie die Optionen Temperaturabhängige Plastizität, Temperaturabhängig-isotrop, Viskoplastisch oder Viskoelastisch im Dropdown-Feld Materialmodell ausgewählt haben, geben Sie die erforderlichen Informationen auf der Registerkarte Thermisch ein.
- Klicken Sie auf OK.