Sobre as definições de espirais

Em seu relacionamento com outras tangentes e curvas, cada espiral é uma curva para dentro ou uma curva para fora.

Os dois parâmetros utilizados com mais frequência por engenheiros no projeto na definição de uma espiral são L (comprimento da espiral) e R (raio de curva circular).

As ilustrações a seguir mostram os diversos parâmetros de uma espiral:

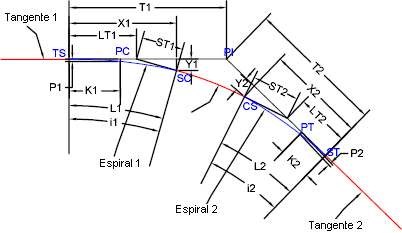
Parâmetros de espiral	Descrição
i1	O ângulo de curva espiral L1, que é o ângulo da espiral.
i2	O ângulo de curva espiral L2, que é o ângulo da espiral.
T1	A distância tangente total de PI para TS.
T2	A distância tangente total de PI para ST.
X1	A distância tangente em SC de TS.
X2	A distância tangente em CS de TS.
Y1	A distância de deslocamento da tangente em SC de TS.
Y2	A distância de deslocamento da tangente em CS de TS.
P1	O deslocamento da tangente inicial no PC da curva invertida.
P2	O deslocamento da tangente inicial fora do PT para a curva invertida.
K1	Da abscissa do PC invertido para o TS referido.
K2	Da abscissa do PT invertido para o ST referido.
LT1	A espiral da tangente longa para dentro.
LT2	A espiral da tangente longa para fora.
ST1	A espiral da tangente curta para dentro.
ST2	A espiral da tangente curta para fora.
	Outros parâmetros de espiral
A1	O valor A é igual à raiz quadrada do comprimento da espiral multiplicado pelo raio. Medida A do nivelamento da espiral.
A2	O valor A é igual à raiz quadrada do comprimento da espiral multiplicado pelo raio. Medida A do nivelamento da espiral.

Fórmula

Espiral composta

As espirais compostas fornecem uma transição entre duas curvas circulares com raios diferentes. Como com a espiral simples, isso permite a continuidade da função da curvatura e fornece uma forma para introduzir uma transição suave na superelevação.

Espiral Cornu

O AutoCAD Civil 3D suporta diversos tipos de espiral, mas a espiral Cornu é o tipo de espiral mais comumente utilizado. A espiral Cornu é utilizada mundialmente em projetos de rodovias e ferrovias.

Primeiro investigada pelo matemático suíço, Leonard Euler, a função de curvatura Cornu é uma função linear escolhida para que a curvatura seja 0 (zero) como um função do comprimento onde a espiral encontra a tangente. A curvatura então aumenta linearmente até que seja igual a curva adjacente no ponto onde a espiral e curva se encontram.

Tal alinhamento fornece a continuidade da função de posição e sua primeira derivada (azimute local), assim como uma tangente e curva fazem em um ponto de curvatura (PC). No entanto, diferente da curva simples, ela também mantém a continuidade da segunda derivada (curvatura local), que se torna cada vez mais importante em velocidades superiores.

Fórmula

As espirais Cornu podem ser expressas como:

Grau plano da espiral:

Ângulo total subentendido por espiral:

A distância tangencial no ponto de espiral-curva do ponto tangente-espiral é:

Distância de deslocamento da tangente no ponto de espiral-curva do ponto tangente-espiral é:

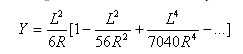
Espiral Bloss

Em vez de usar a Cornu, a espiral Bloss espiral com a parábola de quinto grau pode ser usada como uma transição. Esta espiral tem uma vantagem sobre a Cornu, no sentido que o P Invertido é menor e, portanto, há uma transição mais longa, como um extensão menor da espiral (K). Este fator é importante em projetos de ferrovia.

Fórmula

As espirais Bloss podem ser expressas como:

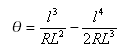
Outras principais expressões:

A distância tangencial no ponto de espiral-curva do ponto tangente-espiral é:

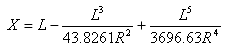
Distância de deslocamento da tangente no ponto de espiral-curva do ponto tangente-espiral é:

Curvas senoidais

Estas curvas representam um curso consistente de uma curvatura e são aplicáveis à transição de 0 a 90 graus de deflexões de tangente. No entanto, as curvas senoidais não são utilizadas habitualmente porque são mais acentuadas que a de uma verdadeira espiral e, portanto, são difíceis de tabular e calcular.

Fórmula

As espirais senoidais podem ser expressas como:

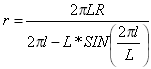
onde r é o raio da curvatura em qualquer determinado ponto.

Espiral senoidal de meio comprimento diminuindo na curva e tangente

Esta forma de equação é normalmente usada no Japão para projeto de ferrovia. Esta curva é útil em situações onde você precisa de uma eficiente transição na alteração da curvatura para baixos ângulos de deflexão (em relação à dinâmica do veículo).

Fórmula

Espiral senoidal de meio comprimento diminuindo na curva e tangente pode ser expressa como:

onde e x é a distância do início para qualquer ponto na curva e é medida ao longo da tangente inicial (estendida); X é o total de X no final da curva de transição.

Outras principais expressões:

A distância tangencial no ponto de espiral-curva do ponto tangente-espiral é:

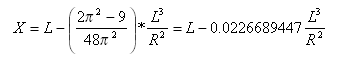
Distância de deslocamento da tangente no ponto de espiral-curva do ponto tangente-espiral é:

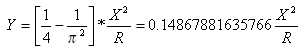
Parábolas cúbicas

As parábolas cúbicas convergem menos rapidamente do que espirais cúbicas, o que torna seu uso popular em projetos de ferrovias e rodovias.

Fórmula

Raio mínimo da parábola cúbica

O raio em qualquer ponto na parábola cúbica é:

Uma parábola cúbica alcança o mínimo r em:

So

O raio de uma parábola cúbica diminui de infinito para em 24 graus, 5 minutos, 41 segundos e, em seguida, em diante começa a aumentar novamente. Isso torna as parábolas cúbica inúteis para deflexões maiores que 24 graus.

Cúbica (JP)

Essa transição foi desenvolvida para os requisitos no Japão. Algumas aproximações da Cornu foram desenvolvidas para usar em situações para acomodar um pequena ângulo de deflexão ou um raio grande. Uma desses aproximações, usada para projetos no Japão, é a Cúbica (JP).

Fórmula

A Cúbica (JP) pode ser expressa como:

Onde X = a distância tangencial no ponto de espiral-curva do ponto tangente-espiral.

Esta fórmula também pode ser expressa como:

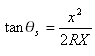
Onde é o ângulo central da espiral (mostrado como i1 e i2in na ilustração)

Outras principais expressões:

A distância tangencial no ponto de espiral-curva do ponto tangente-espiral é:

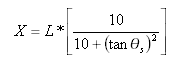
Distância de deslocamento da tangente no ponto de espiral-curva do ponto tangente-espiral é:

Parábola cúbica NSW

Este é um tipo de parábola cúbica modificada para atender os requisitos das normas de New South Wales (Austrália).

Fórmula

A parábola cúbica NSW pode ser expressa como:

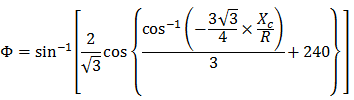
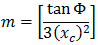
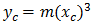
Onde:

Φ = ângulo entre a linha radial final em R e a linha perpendicular para a tangente inicial

R = raio da curva

X_c = total X da espiral determinada

Espirais bi-quadráticas (Schramm)

As espirais bi-quadráticas (Schramm) têm valores baixos de aceleração vertical. Eles contêm duas parábolas de segundo grau cujo raio varia como uma função do comprimento da curva.

Fórmula de curva simples

Curvatura da primeira parábola:

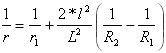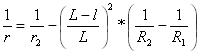para