Ein Spline ist eine glatte Kurve, die durch oder in der Nähe einer Reihe von Punkten verläuft, die Einfluss auf die Form der Kurve haben.
Vorgabemäßig besteht ein Spline aus einer Reihe verschmolzener Kurvensegmente von Grad-3-Polynomen (bzw. kubischen Polynomen). Diese Kurven werden technisch als Nonuniform Rational B-Splines (NURBS) bezeichnet, heißen der Einfachheit halber aber Splines. Kubische Splines sind die gängigsten Splines. Sie ahmen die manuell mit flexiblen Streifen erstellten Splines nach, die durch Gewichtungen an Datenpunkten geformt werden.
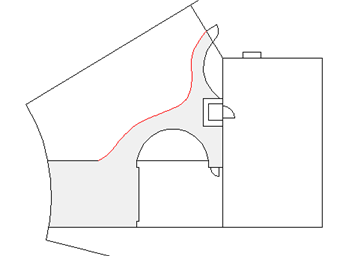
Im folgenden Beispiel wird mit einem Spline die Begrenzung des Betonfußwegs hervorgehoben.
Informationen über Kontrollscheitelpunkte und Anpassungspunkte
Sie können Splines mithilfe von Kontrollscheitelpunkten oder Anpassungspunkten erstellen oder bearbeiten. Der linke Spline zeigt Kontrollscheitelpunkten entlang eines Kontrollpolygons, der rechte Spline zeigt Anpassungspunkte.
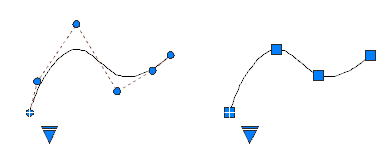
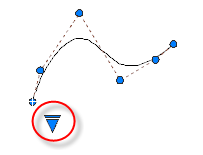
Mit dem dreieckigen Griff auf einem ausgewählten Spline können Sie zwischen der Anzeige der Kontrollscheitelpunkte und der Anzeigen der Anpassungspunkte umschalten. Mit den runden und quadratischen Griffen können Sie einen ausgewählten Spline ändern.
Erstellen von Splines mit Anpassungspunkten
Beim Erstellen von Splines mithilfe von Anpassungspunkten verläuft die resultierende Kurve durch die angegebenen Punkte. Die Form wird dabei durch den Abstand der mathematischen Knoten in der Kurve beeinflusst.
Sie können den Abstand der Knoten mit der Option Knotenparametrisierung wählen. Dies ergibt wie im Beispiel dargestellt andere Kurven.
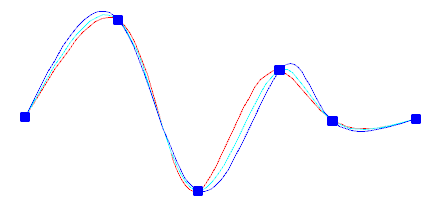
Wenn der Toleranzwert auf 0 eingestellt ist, verläuft der Spline direkt durch die Anpassungspunkte. Mit höheren Toleranzwerten verläuft der Spline in der Nähe der Anpassungspunkte. Sie können optional die Tangentenrichtung des Splines an jedem Ende angeben.
Sonderfälle
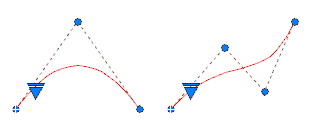
Sie können einen Spline mit einer parabolischen Form erstellen, indem Sie einen Grad-2-Spline angeben, der wie links abgebildet mit genau drei Kontrollscheitelpunkten erstellt wurde. Mit vier Kontrollscheitelpunkten erstellte Grad-3-Splines haben die gleiche Form wie die rechts abgebildeten Bezier-Kurven mit Grad 3.