Parametry analizy modalnej (solwer iteracyjny)

Parametry analizy modalnej można zdefiniować dla nowego przypadku dynamicznego w konstrukcji w jeden z następujących sposobów:

• Wybierz przypadek analizy modalnej w oknie dialogowym Nowy przypadek i kliknij OK.
• Wybierz przypadek analizy modalnej w oknie Typ analizy i naciśnij opcję Ustaw parametry.

Stosowanie solwera iteracyjnego zalecane jest przy rozwiązywaniu dużych zadań. Solwer iteracyjny obejmuje trzy metody rozwiązywania problemów wartości własnych. Poniższe okno dialogowe jest uruchamiane, gdy do rozwiązania układu równań został wybrany solwer iteracyjny (okno dialogowe Preferencje zadania/Analiza konstrukcji).

Uwaga: W programie Robot dostępny jest również drugi rodzaj analizy modalnej: Analiza modalna z uwzględnieniem sił statycznych.

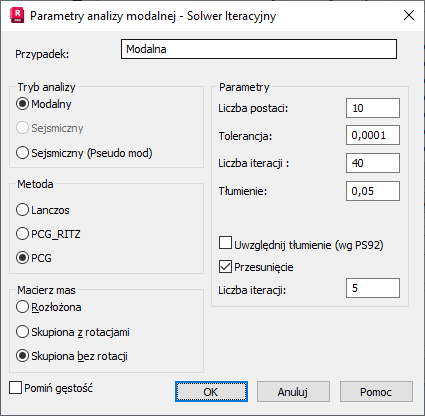
Tryb analizy

W obecnej wersji dla solwera iteracyjnego dostępne są tryby: modalny i sejsmiczny (pseudomodalny). Tryb modalny dostępny jest tylko dla metody gradientu sprzężonego z zastosowaniem ‘preconditioning’ (preconditioned conjugate gradient method — PCG) [1—4]; tryb sejsmiczny (pseudomodalny) dostępny jest zarówno dla zmodifikowanej metody Lanczosa i metody gradientów Ritza (PCG_Ritz — Ritz—gradient method).

Metoda

Metoda Lanczosa

Lanczos jest zmodyfikowaną metodą Lanczosa pozwalającą na uniknięcie faktoryzacji macierzy dużych rozmiarów. Metoda gradientu sprzężonego (PCG) stosowana jest do składania zbioru wektorów Lanczosa zamiast do przeprowadzania rozkładu „odwrotnego” (back resolution) faktoryzowanej macierzy sztywności. Dostępne są wszystkie typy ‘preconditioningu’ (okno dialogowe: Narzędzia > Preferencje zadania > Iteracyjny > Parametry) zdefiniowane dla analizy statycznej.

Metoda Lanczosa jest zalecana w przypadku analizy sejsmicznej i spektralnej dużych konstrukcji, gdy wymagane jest wiele postaci.

• Wymagane parametry

  Typ macierzy mas (skupiona z rotacjami lub rozłożona) i liczba postaci.

  Precyzja obliczeń uzależniona jest od tolerancji przyjętej dla obliczeń wektorów Lanczosa i liczby postaci. Tolerancja przypisywana jest w oknie dialogowym otwieranym po wybraniu z menu polecenia Narzędzia > Preferencje zadania > Iteracyjny > Parametry i jest taka sama jak dla przypadków statycznych. Tolerancja w oknie dialogowym Parametry analizy modalnej – Solwer iteracyjny oznacza tolerancję rozwiązania ogólnego problemu wartości własnych obejmującego zdefiniowane wektory Lanczosa i nie może być mniejsza niż 1.0e—04.

  Im większa Liczba postaci zostanie uwzględniona, tym bliższe odpowiednim wartościom własnym będą małe wektory Ritza. Suma mas modalnych będzie wtedy bardziej dokładna.

PCG_Ritz

PCG_Ritz jest to metoda Ritza, w której podejście gradientu z zastosowaniem ‘preconditioningu’ używane jest do generacji zbioru wektorów bazowych (metoda gradientu Ritza [5]). Stosowanie metody PCG_Ritz jest zalecane w celu przybliżonej, szybkiej definicji par własnych podczas analizy sejsmicznej i spektralnej. Konieczne jest wybranie metody wielopoziomowej. Zaleca się przypisanie jednego poziomu agregacji — metoda ta będzie skuteczna w przypadku problemów średniej wielkości (do 60 000 równań). Dostępne są wszystkie typy ‘preconditioningu’ zdefiniowane dla analizy statycznej (Narzędzia > Preferencja zadania > Iteracyjny > Parametry).

• Wymagane parametry

  Typ macierzy mas (skupiona z rotacjami lub rozłożona) i liczba postaci. Precyzja obliczeń uzależniona jest od Liczby postaci.

PCG

PCG jest metodą gradientu sprzężonego z zastosowaniem ‘preconditioningu’ [1—5]. Zalecana jest w przypadku definiowania małej liczby postaci własnych. Na przykład metoda PCG może być bardzo przydatna podczas przykładania obciążeń wiatrem lub przy sprawdzaniu niewielkiej liczby małych postaci otrzymanych metodą PCG_Ritz. Dostępne są wszystkie typy ‘preconditioningu’ (okno dialogowe: Narzędzia > Preferencje zadania > Iteracyjny > Parametry) zdefiniowane dla analizy statycznej. Mogą być stosowane wszystkie typy macierzy mas (rozłożona, skupiona z rotacjami, skupiona bez rotacji).

• Wymagane parametry:

  Liczba postaci; Tolerancja — kryteria precyzji dotyczące zatrzymania iteracji; Liczba iteracji — maksymalna dopuszczalna liczba iteracji dla każdej postaci (proces iteracji dla każdej postaci jest zatrzymywany, gdy aktualny parametr tolerancji jest mniejszy niż Tolerancja lub gdy aktualna liczba iteracji przekracza Liczbę iteracji); Przesunięcie — umożliwia wykorzystanie techniki przesunięcia dla przyspieszenia zbieżności; Liczba powtórzeń — parametr ten określa liczbę powtórzeń (dla każdej postaci algorytm dokonuje iteracji określonych przez Liczbę iteracji, poprawia wartość przesunięcia i powtarza iteracje określone Liczbą iteracji taką ilość razy, jaką określa Liczba powtórzeń).

• Zalecane parametry:

  Zalecane parametry: metoda wielopoziomowa lub niewielopoziomowa z podejściem ICCF (okno dialogowe: Narzędzia / Preferencje zadania / Iteracyjny / Parametry); liczba postaci £ 5; Tolerancja = 0.01; Liczba iteracji = 100 dla metody niewielopoziomowej; Przesunięcie — wyłączony

  • Typ macierzy mas
  • Parametry (liczba postaci, tolerancja, liczba iteracji, tłumienie).
  • Przesunięcie (z liczbą iteracji).

Zapobieganie nieprawidłowym ustawieniom solwera interacyjnego

W programie został wprowadzony system kontroli, który pozwala zapobiec błędnemu ustawieniu parametrów analizy modalnej dla solwera iteracyjnego. Jest uruchamiany po wciśnięciu przycisku OK w powyższym oknie dialogowym. Na ekranie pojawia się komunikat dotyczący parametrów analizy. Naciśnięcie przycisku Tak powoduje zaakceptowanie wartości parametrów określonych w oknie dialogowym. W przeciwnym razie (po wciśnięciu przycisku Nie) następuje powrót do okna dialogowego Parametry analizy modalnej, aby można było poprawić wartości parametrów.

Jeżeli w obliczeniach używany jest solwer iteracyjny w trybie Sejsmiczny (pseudomodalny), to:

1. Liczba poziomów agregacji powinna być równa 1 (parametr jest podawany w oknie dialogowym Preferencje zadania > Analiza konstrukcji > Parametry > Iteracyjny)
2. Poszukiwaną liczbę postaci należy wpisać co najmniej trzykrotnie większą niż potrzebna liczba postaci.
3. Zbieżność rozwiązania należy sprawdzić dla liczby postaci podanej w punkcie 2 oraz dwukrotnie większej liczby postaci. W przypadku braku zbieżności (wyraźnie inne wartości własne dla dwukrotnie większej liczby postaci niż dla liczby wyjściowej) należy jeszcze zwiększyć liczbę postaci. Po uzyskaniu zbieżnego rozwiązania można użyć filtrowania postaci w celu ograniczenia ich liczby.

Ponadto w przypadku takiego typu analizy parametr Tolerancja w wynikach dynamiki nie ma praktycznego znaczenia (można go zignorować). W przypadku nieprzestrzegania tych zaleceń wyniki mogą być niedokładne (błąd do kilkudziesięciu procent).

Materiały referencyjne

1. Gambolati G., Pini G., Sartoretto F., An improved iterative optimization technique for the leftmost eigenpairs of large symmetric matrice, J. Comp. Phys., 74: 41 — 60, 1988.
2. Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Phys., 81: 53 — 69, 1989.
3. Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Meth. Appl. Mech. Eng., 62: 195 — 207, 1987.
4. M.Papadrakakis, Solving large—scale problems in mechanics, John Wiley & Sons Ltd., 1993.
5. Fialko S., High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis, CAMES, 7: 537-550, 2000.

Zobacz także:

Założenia przyjmowane w analizie modalnej konstrukcji

Parametry analizy modalnej z uwzględnieniem sił statycznych

Opis analizy modalnej z uwzględnieniem sił statycznych

Opis metody blokowej iteracji podprzestrzennej

Analiza modalna — dokładność obliczeń

Parametry solwera iteracyjnego

Solwery dostępne w programie Robot