Solwery iteracyjne

Istnieje kilka typów solwerów iteracyjnych.

Iteracyjny ICCF

Metoda ta jest zalecana dla dużych problemów z małą liczbą po prawej stronie.

• Użycie pamięci: wysokie.
• Użycie dysku: brak.
• Prędkość szacunkowa: wysoka (dla dobrze uwarunkowanych problemów).
• Liczba równań: 15 000–1 000 000 i więcej równań.
• Obsługiwane analizy: statyka liniowa, analiza modalna, wyboczenia.
• Ograniczenia dostępnych analiz: nie dotyczy.
• Inne ograniczenia:
  • Poprawność ograniczeń konstrukcji nie jest sprawdzana.
  • Wolna zbieżność, jeśli niektóre problemy są nieprawidłowo uwarunkowane.

Przekątna iteracyjna

Metoda ta jest zalecana dla dużych problemów z małą liczbą po prawej stronie.

• Użycie pamięci: minimalne
• Użycie dysku: minimalne
• Prędkość szacunkowa: niska
• Liczba równań: 15 000–1 000 000 i więcej równań.
• Obsługiwane analizy: statyka liniowa, analiza modalna, wyboczenia.
• Ograniczenia dostępnych analiz: nie dotyczy
• Inne ograniczenia:
  • Poprawność ograniczeń konstrukcji nie jest sprawdzana.
  • Wolna zbieżność, jeśli niektóre problemy są nieprawidłowo uwarunkowane.

Iteracyjna metoda Gauss-Cholesky

Ta metoda jest zalecana dla dużych problemów z małą liczbą po prawej stronie, jeśli nie ma wystarczającej ilości pamięci RAM, aby użyć metody ICCF.

Weryfikacja macierzy każdego elementu jest wykonywana za pomocą procedury oszacowania Vinget. ¹².

• Użycie pamięci: minimalne
• Użycie dysku: minimalne
• Prędkość szacunkowa: niska
• Liczba równań: 15 000–1 000 000 i więcej równań.
• Obsługiwane analizy: statyka liniowa, analiza modalna, wyboczenia.
• Ograniczenia dostępnych analiz: nie dotyczy
• Inne ograniczenia:
  • Poprawność ograniczeń konstrukcji nie jest sprawdzana.
  • Wolna zbieżność, jeśli niektóre problemy są nieprawidłowo uwarunkowane.

Iteracyjna wielopoziomowa metoda ICCF

Metoda ta jest zalecana dla dużych problemów z małą liczbą po prawej stronie. Wykazuje szybszą zbieżność niż iteracyjna metoda ICCF.

• Użycie pamięci: wysokie
• Użycie dysku: minimalne
• Prędkość szacunkowa: wysoka dla dobrze uwarunkowanych problemów
• Liczba równań: 15 000–1 000 000 i więcej równań.
• Obsługiwane analizy: statyka liniowa, analiza modalna, wyboczenia.
• Ograniczenia dostępnych analiz: dostępne typy konstrukcji: 3D (pręty, powłoki, bryły i wszystkie specjalne elementy skończone), ramy 2D.
• Inne ograniczenia:
  • Poprawność ograniczeń konstrukcji nie jest sprawdzana.
  • Mniej stabilna zbieżność (w kilku przypadkach).

Iteracyjna wielopoziomowa przekątna

Ta metoda jest znacznie wolniejsza niż iteracyjna metoda wielopoziomowa ICCF. Jednakże wymaga znacznie mniej pamięci RAM.

Metoda wygładzania 2 zazwyczaj wymaga mniej iteracji w porównaniu do iteracyjnej wielopoziomowej metody ICCF.

Weryfikacja macierzy każdego elementu jest wykonywana za pomocą procedury oszacowania Vinget ^1,2.

• Użycie pamięci: minimalne
• Użycie dysku: minimalne
• Prędkość szacunkowa: niska
• Liczba równań: 15 000–1 000 000 i więcej równań.
• Obsługiwane analizy: statyka liniowa, analiza modalna, wyboczenia.
• Ograniczenia dostępnych analiz: dostępne typy konstrukcji: 3D (pręty, powłoki, bryły i wszystkie specjalne elementy skończone), ramy 2D.
• Inne ograniczenia:
  • Poprawność ograniczeń konstrukcji nie jest sprawdzana.

Iteracyjna metoda wielopoziomowa Gauss-Cholesky

Ta metoda jest znacznie wolniejsza niż iteracyjna metoda wielopoziomowa ICCF. Jednakże wymaga znacznie mniej pamięci RAM.

Metoda wygładzania 2 zazwyczaj wymaga mniej iteracji w porównaniu do iteracyjnej wielopoziomowej metody ICCF.

Weryfikacja macierzy każdego elementu jest wykonywana za pomocą procedury oszacowania Vinget ^1,2.

• Użycie pamięci: minimalne
• Użycie dysku: minimalne
• Prędkość szacunkowa: średnia (dla dobrze uwarunkowanych problemów)
• Liczba równań: 15 000–1 000 000 i więcej równań.
• Obsługiwane analizy: statyka liniowa, analiza modalna, wyboczenia.
• Ograniczenia dostępnych analiz: dostępne typy konstrukcji: 3D (pręty, powłoki, bryły i wszystkie specjalne elementy skończone), ramy 2D.
• Inne ograniczenia:
  • Poprawność ograniczeń konstrukcji nie jest sprawdzana.

Obliczenia według metody iteracyjnej

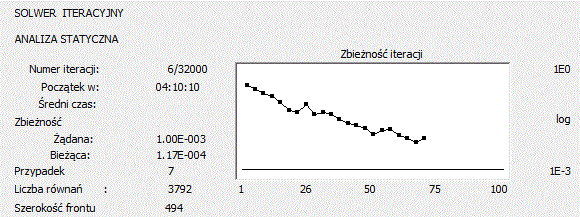
W oknie dialogowym obliczeń dla metody iteracyjnej pokazywany jest proces zbieżności metody iteracyjnej, jeśli zostanie osiągnięty zdefiniowany przez użytkownika poziom dokładności lub jeśli proces jest rozbieżny.

Wykres pokazuje również następujące informacje:

• Liczba aktualnie wykonywanych iteracji / maksymalna liczba iteracji.
• wymagana dokładność,
• dokładność bieżącej iteracji,
• liczba równań,
• szerokość frontu.