Modo de análise de estrutura dinâmica

As características dos modos de análise de estruturas modal, sísmica e sísmica (pseudo) são mostradas abaixo.

Modo modal:

Essa abordagem permite a análise modal da estrutura, definindo os primeiros n valores e vetores próprios da estrutura.

Os métodos de análise disponíveis são: iteração de subespaço, método de Lanczos e método de redução de base.

As iterações serão concluídas se a seguinte condição for atendida:

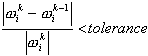
em que: i = 1,2,...,n modos de vibração, k – número de iterações.

O limite superior é o valor do período (pulsação, frequência) que descreve que no intervalo (0, limite superior) os seguintes valores e vetores próprios serão definidos.

A verificação de Sturm, que permite localizar as pulsações ignoradas, é possível.

Modo sísmico

Para a análise de estruturas sísmica e espectral, não é essencial que os valores e vetores próprios sejam organizados em ordem. É importante apenas que os valores e vetores próprios caracterizados por um grande coeficiente de participação de massa (com um efeito significativo na resposta sísmica) sejam considerados.

Nesse modo, são definidos n valores e vetores próprios da estrutura. Os valores definidos não são organizados em ordem e alguns valores e vetores podem ser omitidos.

Métodos de análise disponíveis: método de Lanczos.

Método de convergência:

em que:

Φ _i – i-ésimo vetor próprio

Limite superior em que os limites são ignorados.

A verificação de Sturm não é executada para esse modo de análise de estrutura.

Modo sísmico (pseudomodal)

Esse modo é usado somente para análises espectral e sísmica. Deve ser usado para métodos de análise clássicos com base em resultados de decomposição modal com tempos de análise de estrutura muito demorados. Esse método consiste em apresentar o vetor da solução X como uma sobreposição de determinados vetores de base que não representam a aproximação exata do modo Φ _i .

Métodos de análise disponíveis: método de Lanczos.

A verificação de Sturm não é executada para esse modo de análise de estrutura.

Nota: Para estruturas separadas, não é possível usar o método de Lanczos porque é necessária uma matriz tridiagonal em T que não seja de um tipo consistente, enquanto uma matriz em T de estrutura separada é de um tipo consistente.

Quando o método de Lanczos é selecionado em um programa, o programa altera o método de cálculo para um método de iteração de subespaço. Para usar o método de Lanczos nos cálculos, as estruturas separadas devem ser conectadas de forma que um modelo de estrutura não seja alterado (por exemplo, uma barra entre os apoios deve ser adicionada).