A análise do histórico de tempo obtém a reação da estrutura em pontos de tempo selecionados para uma interação duradoura definida. Isso é contrário a outros tipos de análise disponíveis que mostram a reação da estrutura na forma de amplitudes obtidas por um único momento.
A análise do histórico de tempo consiste em encontrar uma solução para a seguinte equação da variável de tempo “t”:
M * a(t) + C * v(t) + K * d(t) = F(t)
em que os seguintes valores iniciais são conhecidos: d(0)=d0 e v(0)=v0.
onde:
M – matriz de massa.
K –matriz de rigidez.
C = a * M + b * K – matriz de amortecimento.
α – coeficiente definido pelo usuário.
β – coeficiente definido pelo usuário.
d – vetor de deslocamento.
v – vetor de velocidade.
a – vetor de aceleração.
F – vetor de carga.
Todas as expressões que contêm o parâmetro (t) dependem do tempo.
O método Newmark ou o método de decomposição é usado para resolver a tarefa apresentada acima. O método Newmark pertence ao grupo de algoritmos que são incondicionalmente convergentes para parâmetros de método definidos de forma apropriada. Ele usa as seguintes fórmulas para calcular os deslocamentos e a velocidade na próxima etapa de integração.
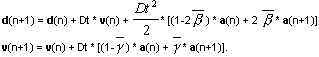
Os parâmetros β e γ controlam a convergência e a precisão dos resultados obtidos por meio do método.
A convergência incondicional é garantida para 0,5 ≤ γ 2≤ * b.
Os valores b = 0,25 e g = 0,5 são adotados. A modificação desses valores será possível, mas somente se a análise linear do histórico de tempo com o método Newmark ou Newmark (aceleração) ativado for usada. Esses valores (TransBeta e TransGama) podem ser alterados no arquivo de preferência *.COV salvo na pasta CFGUSR. Para executar cálculos para diferentes valores dos parâmetros b e g, é necessário alterar os parâmetros TransBeta e TransGama no arquivo *.COV e carregar esse arquivo de preferência.
É aconselhável usar o método Newmark para históricos de curto prazo quando uma carga concentrada é aplicada à estrutura. Tais cargas induzirão um movimento que exigirá um grande número de modos de elevação para ser descrito. Portanto, o método Newmark será mais eficiente do que o método de decomposição modal para esse tipo de tarefa. O método Newmark aproveita as equações iniciais sem qualquer simplificação. A precisão dos resultados obtidos depende da precisão da integração numérica das equações de tempo e é definida pelo valor do intervalo de tempo para os parâmetros selecionados: α, β. O método não requer que o problema próprio seja resolvido para obter os valores próprios e os vetores próprios. Para longos históricos, porém, o método é muito demorado. No caso de tais tarefas, os cálculos devem ser executados para um grande número de intervalos de tempo com a precisão necessária.
O método Hilber-Hughes-Taylor (HHT) implementa o amortecimento numérico de frequências mais altas sem a perda da precisão da solução. Uma forma discreta da equação do histórico de tempo é como segue.
onde:
-1/3 ≤ α ≤ 0
Assumindo:
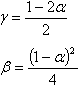
um esquema de integração incondicionalmente estável com precisão de segunda ordem é obtido.
Para o modo de aceleração, os valores de avaliação na etapa de integração n+1 são determinados como segue.
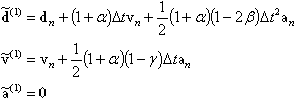
O método HHT é um algoritmo muito eficiente para a integração numérica que permite remover o impacto desfavorável de altas frequências na qualidade de uma solução.
O método de decomposição modal é um método simples de obter a solução necessária. Ele se baseia na representação do movimento da estrutura como uma superposição do movimento das formas não acopladas. Portanto, o método requer que valores próprios e vetores próprios sejam determinados. O método Lanczos é recomendado para esta finalidade, seguido pela verificação Sturm. O método de decomposição modal aproveita a redução de equações não acopladas.
A equação (sem amortecimento) pode ter a seguinte forma:
onde
![]() ,
,
Ng – número de “grupos de carga”, φk(t) – histórico de tempo para o grupo de carga k-th
![]() (2)
(2)
Ao inserir a equação (2) na equação (1) e reconhecer o amortecimento modal e as condições de ortogonal ![]() , é obtida a seguinte equação.
, é obtida a seguinte equação.
em que ![]() , ξ – parâmetros de amortecimento modal, ωi – frequência para a forma i-ésima.
, ξ – parâmetros de amortecimento modal, ωi – frequência para a forma i-ésima.
Cada uma das equações é resolvida numericamente com a precisão da segunda ordem. O vetor de deslocamento resultante X(t) para os pontos de tempo definidos t* = t1, t2, ... é obtido após a introdução de qi(t*), i=1,2,...,m em equações (2).
Vale a pena observar as diferenças entre os tipos de análise disponíveis descritos neste tópico. A movimentação da análise de carga difere da análise do histórico de tempo, pois não reconhece os efeitos dinâmicos. A diferença entre a análise harmônica e a análise do histórico no tempo consiste em determinar a reação da estrutura exclusivamente na forma de amplitudes e não na forma de uma função de tempo.
Consulte também: