Netze

Bei der Finite-Elemente-Methode wird ein reales Objekt in eine Vielzahl (Tausende bis Hunderttausende) von Elementen, z. B. kleine Tetraeder oder Würfel, zerlegt, das sogenannte Netz. Mit festgelegten mathematischen Gleichungen wird das Verhalten der einzelnen Elemente prognostiziert. Der Computer kombiniert die Verhaltensweisen aller einzelnen Elemente, um das Verhalten des gesamten Bauteils oder der Baugruppe zu prognostizieren.

Die Qualität des Flächennetzes und die Formen der Volumenkörperelemente haben Einfluss auf die Genauigkeit der Simulationsergebnisse. Die Dichte des Netzes (d. h. die Anzahl von Elementen pro Volumeneinheit) beeinflusst die Genauigkeit der Ergebnisse ebenfalls. Achten Sie auf die Netzqualität und die lokale Netzverfeinerung, um die Genauigkeit Ihrer Ergebnisse mittels Netzkonvergenz-Techniken zu maximieren.

Autodesk Fusion ermöglicht die automatische Netzgenerierung mit globalen und lokalen Einstellungen für Netzgröße, -qualität, Elementreihenfolge und andere Optionen.

• Netzeinstellungen gelten für alle Komponenten.
• Lokale Netzsteuerungen gelten für ausgewählte Objekte.
• Jede Simulationsstudie hat eigene Netzeinstellungen.

Bei einem guten Netz erfolgt eine Abwägung zwischen Genauigkeit und Berechnungszeit. Hochwertige Netze konvergieren schnell, führen zu genauen Ergebnissen und nicht zu Fehlern. Der Großteil des Netzerstellungsprozesses umfasst die Angabe der gewünschten Netzeinstellungen.

Knoten und Elemente

Vor dem Lösen einer Fusion-Analyse wird die Geometrie in kleine Bestandteile aufgeteilt, die als Elemente bezeichnet werden. Die Ecke jedes Elements wird als Knoten bezeichnet. Die Berechnung wird an den Knoten durchgeführt. Darüber hinaus können Knoten am Mittelpunkt der Kanten der Elemente enthalten sein. Das Netz wird aus diesen Elementen und Knoten gebildet.

Die Lösungsgenauigkeit hängt von einem geeigneten Netz ab. Fusion automatisiert deshalb einen Großteil des Netzerstellungsprozesses, damit Sie ein geeignetes Netz für die Simulation erstellen können.

Ein Knoten ist eine Koordinatenposition im Raum, für die Freiheitsgrade (DOFs) definiert sind. In strukturellen Analysen stellen die Freiheitsgrade die möglichen Bewegungen des Punkts aufgrund der Belastung der Struktur dar. Die Materialdehnung wird durch die relative Bewegung der Knoten bestimmt, und die Spannungen werden basierend auf den Dehnungen und den Materialeigenschaften berechnet. Bei thermischen Analysen ist der einzige Freiheitsgrad die Temperatur an jedem Knoten. Der Wärmestrom wird dann basierend auf der Temperaturverteilung und der thermischen Leitfähigkeit des Materials bestimmt. Die Freiheitsgrade bestimmen auch, welche Kräfte und Momente von einem Element auf das nächste übertragen werden. Die Ergebnisse einer Finite-Element-Methode (Verformungen, Spannungen, Temperaturen und Wärmestromgeschwindigkeit) werden an den Knoten angegeben.

In der realen Welt wird ein Punkt in sechs verschiedene Richtungen bewegt - Verschiebung in X, Y und Z sowie Rotation um X, Y und Z. In FEM kann ein Knoten aus verschiedenen Gründen in den berechneten Bewegungen beschränkt werden. Beispielsweise ist es nicht erforderlich, für ein 2D-Element die Verschiebung außerhalb der Ebene zu berechnen. Es ist kein 2D-Element, wenn die Knoten außerhalb der Ebene verschoben werden können. Darüber hinaus werden Knotendrehungen für Volumenkörper nicht berücksichtigt. Alle Verformungen in Volumenkörperelemente sind ausschließlich das Ergebnis von Knotenübertragungen. Alle planaren und Linienelemente unterstützen in der Regel jedoch Rotationsfreiheitsgrade.

Der Freiheitsgrad eines Knotens bezieht sich darauf, welche Arten von Kräften, Beschränkungen oder Wärmeströmen durch den Knoten auf das Element übertragen werden. Eine Kraft - axial oder Scherung - entspricht einem Freiheitsgrad für Verschiebung, da die Steifheit des Elements bestimmt, wie weit sich ein Knoten bewegt, wenn eine bestimmte Last auf ihn angewendet wird. Ein Moment entspricht einem Rotationsfreiheitsgrad. Um also einen Moment um eine bestimmte Achse zu übertragen, muss der Knoten einen Freiheitsgrad für Drehung um die Achse aufweisen. Wenn ein Punkt nicht über einen Freiheitsgrad für Drehung verfügt, hat das Anwenden eines Moments auf den Knoten keine Auswirkungen auf die Analyse. Auch das Beschränken eines Knotens mit einer Randbedingung für Drehung hat keine Auswirkungen, wenn der Knoten das Moment nicht übertragen kann.

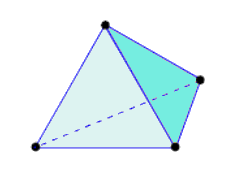
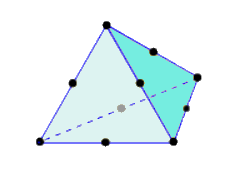
Ein Element ist der Grundstein der Finite-Elemente-Methode. Es gibt verschiedene Elementtypen, und ihre Verwendung hängt vom Modell und vom Analysetyp ab. Aktuell sind alle Volumenkörperelemente in Fusion Tetraederelemente (die jeweils vier dreieckige Flächen und sechs Kanten umfassen). Lineare Tetraederelemente haben vier Knoten. Parabolische Tetraederelemente verfügen außerdem über einen Knoten in der Mitte jeder Kante, sodass sie insgesamt zehn Knoten pro Element aufweisen. Es gibt zwei Varianten der parabolischen Tetraederelemente - mit und ohne gekrümmte Kanten.

Tabelle 1: Varianten von Tetraederelementen.

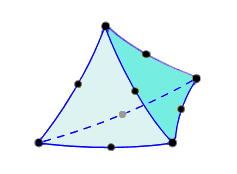Lineares Tetraeder	Parabolisches Tetraeder	Parabolisches Tetraeder mit gekrümmten Kanten
(4 Knoten)	(10 Knoten)	(10 Knoten)

Ein Element ist eine mathematische Beziehung, die definiert, wie sich die Freiheitsgrade eines Knotens auf den nächsten beziehen. Diese mathematische Beziehung definiert auch, wie durch die Verformungen Spannungen erzeugt werden.