You can calculate the intersection between a line and an arc. The line is established by a point, bearing, and offset.
To calculate the intersection of an arc and bearing line in the Survey Command Window
- In Toolspace, on the Survey tab, right-click the network to edit, and click Survey Command Window.
- Click Intersections menu
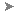Arc/Bearing. - Enter the point identifier of the arc center.
- Enter the radius of the arc.
- Enter the starting point identifier of the line.
- Enter the bearing of the line.
- Enter the quadrant of the line.
- Enter an offset.
- Enter one of the following options:
- N: To select the northern-most intersection.
- S: To select the southern-most intersection.
- E: To select the eastern-most intersection.
- W: To select the western-most intersection.
- R: To select the solution nearest.
- F: To select the solution farthest.
- 1: To select intersection 1.
- 2: To select intersection 2.
- A: To select all the intersections.
- P: To pick the intersection with your pointing device
To calculate the intersection of an arc and bearing line, using the survey command language
- In Toolspace, on the Survey tab, right-click the network to edit, and click Survey Command Window.
- At the Command line, enter:
ARCB [point] [radius] [point 1] [bearing] [quadrant] [offset]
Command Line Example
NE 1 100 100
NE 2 200 200
ARCB 2 200 1 50 1 -50
! INTERSECTION # 1 NORTH:372.285978 EAST:301.575300
! INTERSECTION # 2 NORTH:98.424700 EAST:27.714022
Intersections are located between an arc radius of 200 with its center at point 2 and a bearing of 50.0000 drawn from point 1 with an offset distance of 50 to the left.
Command Syntax
ARCB [point] [radius] [point 1] [bearing] [quadrant] [offset]
| Parameter | Definition |
|---|---|
| point | The radial point. This is an existing point that is used as the center point for the arc. |
| radius | The radial distance. This is the distance in feet or meters from the radial point to the arc. |
| point 1 | The existing point from which a vector extends. It can be any type of point including a figure point. |
| bearing | The bearing of the line from the existing point. A bearing establishes a direction for the vector and is expressed in current angle units. |
| quadrant | The quadrant in which the bearing exists. The possible values are: 1 (NE), 2 (SE), 3 (SW), and 4 (NW). |
| offset | The offset left or right from the vector. This acts as if the line is moved X feet. An offset to the right is a positive number, and an offset to the left is a negative number. If you do not want an offset, then use zero for the offset. |