Durchführen von nichtlinearen Analysen

Siehe auch die Seite Durchführen von Analysen mit Kontakt, wenn die Berechnung irgend eine Art Kontakt umfasst (Fläche-zu-Fläche-Kontakt, Kontakt- oder Kopplungselemente, Aufprallfläche usw.).

Protokolldateien und Konvergenz-Plot für nichtlineare Analysen

Die Hauptfrage bei einer mechanischen Ereignissimulation (MES) und anderen nichtlinearen Analysen ist, ob das Modell konvergiert oder nicht, bzw. wie leicht es konvergiert. Wenn mit der Ausführung der Iterationen begonnen wird, unterstützt Sie die Anzeige des Konvergenzverhaltens bei der Entscheidung, ob Sie die Analyse unterbrechen müssen, um einige Parameter zu ändern.

Auf dieser Seite werden die Spalten beschrieben, aus denen der Konvergenzverlauf besteht und die in der Protokolldatei der Analyse angezeigt werden. Darüberhinaus kann der Konvergenzverlauf grafisch dargestellt werden. Mit der Dropdown-Liste Analyseinformation im Analysefenster können Sie aus den folgenden Optionen auswählen:

Der Konvergenzverlauf wird während der Lösungs-Iterationen in der Protokolldatei gespeichert. Die Spalten, aus denen der Konvergenzverlauf besteht, sind die Folgenden (siehe Tabelle 1):

Insbesondere die aktuelle Zeitschrittgröße DT hängt wie folgt mit der Zeitschrittstufe L zusammen:

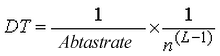
wobei n der Zeitschrittänderungsfaktor ist, der auf der Registerkarte Analysenparameter: Erweitert: Zeitschritt eingegeben wurde. Der Vorgabewert für den Zeitschrittänderungsfaktor ist 2. Um zu errerichen, dass der Zeitschritt schneller reduziert wird (bzw. schneller erhöht wird, wenn das Modell zu konvergieren beginnt), setzen Sie den Zeitschrittänderungsfaktor auf einen größeren Wert.

Zeilennummer Zeit Prozent DT L Iter. Rest
01 0.000000 0.00 0.050000 1 0 0.0000E+00
02 0.050000 2.50 0.050000 1 1 6.3147E-01
03 0.050000 2.50 0.050000 1 2 2.5240E-02
04 0.050000 2.50 0.050000 1 3 4.8034E-04
05 0.050000 2.50 0.050000 1 4 1.3060E-05c
06 0.100000 5.00 0.050000 1 1 1.0000E+00
07 0.075000 3.75 0.025000 2 1  1.5186E-01
08 0.075000 3.75 0.025000 2 2 5.0903E-03
09 0.100000 3.75 0.025000 2 3 1.5940E-05c
10 0.100000 5.00 0.025000 2 1 1.2368E-01
11 0.100000 5.00 0.025000 2 2 3.1349E-03
12 0.100000 5.00 0.025000 2 3 4.5975E-06c
13 0.125000 6.25 0.025000 2 1 1.4627E-01
14 0.125000 6.25 0.025000 2 2 1.2403E-03
15 0.125000 6.25 0.025000 2 3 4.7008E-06c
16 0.150000 7.50 0.025000 2 1  1.8106E-01
17 0.150000 7.50 0.025000 2 2 1.3597E-04
18 0.150000 7.50 0.025000 2 3  4.9347E-07c
19 0.200000 10.00 0.050000 1 1 3.1410E-01
20 0.200000 10.00 0.050000 1 2 5.4314E-03
21 0.200000 10.00 0.050000 1 3 2.5865E-04
22 0.200000 10.00 0.050000 1 4 1.1274E-04
23 0.200000 10.00 0.050000 1 5 2.7762E-05c
Tabelle 1: Beispieltext aus einer Protokolldatei für MES/nichtlineare Spannung

(Die erste Spalte ist nicht Teil der Analyseprotokolldatei. Zeilennummern wurden hinzugefügt, um die folgende Beschreibung übersichtlicher zu machen.)

Vor dem Hintergrund der obigen Erklärung kann die Beispielprotokolldatei wie folgt interpretiert werden:

Anmerkung: Weitere Informationen zur grafischen Darstellung des Konvergenzverlaufs finden Sie auf der Seite Konvergenz-Plot.

Riks-Analyse:

Die Protokolldatei für eine Riks-Analyse ist derjenigen für MES und nichtlineare Spannung (siehe oben) sehr ähnlich. Eine zusätzliche Spalte wird in die Ausgabe angezeigt: die Spalte Laststufe. (Siehe Tabelle 2.) Die Laststufe ist der Multiplikator für alle Knotenkräfte und Momente im Modell.

Zeilennummer Zeit Prozent DT L Iter. Rest Laststufe
01 0.000000 0.00 1.000000 1 0 0.0000E+00  
02 1.000000 0.20 1.000000 1 1 1.0000E+00 1.0000E+00
03 1.000000 0.20 1.000000 1 2 4.0357E-03 1.0000E+00
04 1.000000 0.20 1.000000 1 3 1.0000E-04 1.0000E+00c
05 2.000000 0.40 1.000000 1 1 1.0000E+00 2.0000E+00
06 2.000000 0.40 1.000000 1 2 4.1056E-03 2.0000E+00
07 2.000000 0.40 1.000000 1 3 1.0000E-04 2.0000E+00c
08 3.000000 0.60 1.000000 1 1 1.0000E+00 3.0000E+00
... {Text der Kürze halber entfernt} ...
09 30.000000 6.00 1.000000 1 3 1.0000E-04 3.0000E+01c
10 31.000000 6.20 1.000000 1 1 1.0000E+00 3.1000E+01
11 31.000000 6.20 1.000000 1 2 8.0425E-03 3.1000E+01
12 31.000000 6.20 1.000000 1 3 1.0000E-04 3.1000E+01c
13 32.000000 6.40 1.000000 1 1 1.0000E+00 3.2000E+01
14 32.000000 6.40 1.000000 1 2 8.3103E-03 3.2000E+01
15 32.000000 6.40 1.000000 1 3 1.0000E-04 3.2000E+01c
16 33.000000 6.60 1.000000 1 1 1.0000E+00 3.2693E+01
17 33.000000 6.60 1.000000 1 2 1.0976E-04 1 3.2689E+01
18 33.000000 6.60 1.000000 1 3 1.0000E-04 3.2689E+01c
19 34.000000 6.80 1.000000 1 1 1.0000E+00 3.3373E+01
20 34.000000 6.80 1.000000 1 2 1.1202E-04 3.3369E+01
21 34.000000 6.80 1.000000 1 3 1.0000E-04 3.3369E+01c
22 35.000000 7.00 1.000000 1 1 1.0000E+00 3.4046E+01
23 35.000000 7.00 1.000000 1 2 1.1427E-04 3.4041E+01
24 35.000000 7.00 1.000000 1 3 1.0000E-04 3.4041E+01c
Tabelle 2: Beispieltext aus einer Riks-Analyse-Protokolldatei

(Die erste Spalte ist nicht Teil der Analyseprotokolldatei. Zeilennummern wurden hinzugefügt, um die folgende Beschreibung übersichtlicher zu machen.)

In diesem Beispiel wird der Lastmultiplikator anfangs nach jedem konvergierten Zeitschritt linear um 1 erhöht (Zeilen 04, 07, 09 und 12), basierend auf der vom Benutzer eingegebenen Erhöhung des anfänglichen Lastfaktors von 1. Der nächste Zeitschritt konvergiert ebenfalls in drei Iterationen (Zeile 15). Die Laststufe für den nächsten konvergierten Schritt (Zeile 18) wurde nur um 0.689 (= 32.689-32.000) erhöht. Die nachfolgenden konvergierten Schritte zeigen, dass die Änderungsrate der Laststufe weiter fällt (in den Zeilen 21 und 24 finden sich Erhöhungen um 0.680 bzw. 0.672). Wenn das Modell sich dem Beulen oder Durchbrechen nähert, kann die Laststufe auf 0 fallen und negativ werden.

Häufige Fehlermeldungen bei der nichtlinearen Analyse:

Bei der Ausführung der Analyse können Sie unter Umständen eine Fehler- oder Warnmeldung von den Prozessoren erhalten. Im Folgenden finden Sie eine Liste der häufigen Prozessormeldungen mit einer kurzen Erläuterung.

Tipp: Wenn eine Warnung oder ein Fehler bei ergebnisbasierten Lastkurven auftritt, liegt das häufig daran, dass die Lastkurvenvariablen nicht ordnungsgemäß eingerichtet sind. Viele dieser Fehler sind die Folge von Fehlern in der Gleichung des Suchlaufwerts. Zum Bearbeiten der Gleichung gehen Sie zu Analyse: Parameter und wählen die entsprechende Lastkurve aus. Wählen Sie dann Referenzindizes definieren/bearbeiten, um die Einrichtung des Suchlaufwerts (Referenzindex) zu prüfen.
Fehler (1)
Allgemeiner Fehler, mit dem der Benutzer benachrichtigt wird, dass die Analyse nicht abgeschlossen werden konnte. Gehen Sie von dieser Stelle aus in der Protokolldatei zurück, um einen Hinweis oder sonstigen Text zur Art des Problems zu suchen.
FEHLER: Balkenquerschnitt ist in Bauteil nicht definiert, Nr. = P Abschnitts-ID = L
Ursache: Balkenelemente, die zu einem Abschnittstyp Allgemein (in der Elementdefinition) in Bauteil P zugewiesen wurden, werden auf Schicht Nr. L gezeichnet. Typen des Abschnitts Allgemein unterstützen nur Schicht 1.
Aktion: Ändern Sie alle Zeilen im angegebenen Bauteil zu Schicht 1. (Wählen Sie das Bauteil in der Strukturansicht oder im Anzeigebereich aus, indem Sie Auswahl Auswählen Bauteil verwenden. Klicken Sie dann mit der rechten Maustaste, und wählen Sie Zugehörige auswählen Linien. Ändern Sie die Schichtnummern zu 1, indem Sie mit der rechten Maustaste klicken und Attribute bearbeiten wählen.)
FEHLER: Geteilt durch Null in ergebnisbasierter Lastkurve.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Eine Division durch Null ist beim Auswerten der Gleichung für den Suchlaufwert aufgetreten. Überprüfen Sie die Gleichung auf Genauigkeit und passen Sie sie ggf. an, um zu verhindern, dass ein Wert von Null im Nenner steht.
FEHLER: Leere Klammern in ergebnisbasierter Lastkurve gefunden: Funktion.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Die Syntax der Gleichung für den Suchlaufwert hat ein Problem mit der Gruppierung der Klammern ( ). Überprüfen Sie die Gleichung auf Genauigkeit und korrigieren Sie sie.
FEHLER: mathematischer Fehler, |x| muss kleiner oder gleich 1 in acos(x) sein.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Das Argument der mathematische Funktion liegt außerhalb des zulässigen Bereichs. X muss zwischen -1 und 1 liegen.
FEHLER: mathematischer Fehler, |x| muss kleiner oder gleich 1 in asin(x) sein.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Das Argument der mathematische Funktion liegt außerhalb des zulässigen Bereichs. X muss zwischen -1 und 1 liegen.
FEHLER: mathematischer Fehler, undefiniertes Ergebnis 0**0.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Ein undefinierter Ausdruck wird in der Gleichung des Suchlaufwerts ausgewertet.
FEHLER: mathematischer Fehler, x muss in log(x) positiv sein.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Das Argument der mathematische Funktion liegt außerhalb des zulässigen Bereichs.
FEHLER: mathematischer Fehler, x muss in log10(x) positiv sein.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Das Argument der mathematische Funktion liegt außerhalb des zulässigen Bereichs.
FEHLER: mathematischer Fehler, x muss in sqrt(x) positiv sein.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Das Argument der mathematische Funktion liegt außerhalb des zulässigen Bereichs.
Fehler: negatives aktives Intervall erkannt, Intervallnummer: N
Ursache: Eine Zwangsverschiebung hat einen Beendigungszeitpunkt, der vor oder beim Ursprungszeitpunkt liegt. Der Fehler tritt für Verschiebungen auf, die der aktiven Bereichsnummer N zugewiesen sind.
Aktion: Bearbeiten Sie eine der Zwangsverschiebungen im FEM-Editor und klicken Sie auf die Schaltfläche Daten für das Feld Aktiver Bereich. (Die Tabellenkalkulation Aktiver Bereich wird von allen Zwangsverschiebungen gemeinsam genutzt, sodass es keine Rolle spielt, welche geändert wird.) Die Index-Zeilen entsprechen den aktiven Bereichen aller Zwangsverschiebungen. Ändern Sie für die in der Fehlermeldung angegebene Zeile die Ursprungs- und Beendigungszeitpunkte, sodass die Beendigungszeit nach der Ursprungszeit liegt. Bestätigen Sie auch, dass eine Indexzeile für jeden definierten aktiven Bereich für alle Zwangsverschiebungen vorhanden ist.
FEHLER: ergebnisbasierte Lastkurve unterstützt keine Zwangsverschiebung.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Zwangsverschiebungen und Antriebselemente können keiner ergebnisbasierten Lastkurve zugewiesen werden. Sie müssen einer zeitbasierten Kurve zugewiesen werden.
FEHLER: Abschnitt Typ 1 kann nicht in einem nichtlinearen Bauteil verwendet werden.
Siehe oben: FEHLER: Balkenquerschnitt ist in Bauteil nicht definiert.
FEHLER: Abschnittstyp muss zwischen 2 und 7 liegen. Elementgruppennummer = P, Abschnitts-ID = L
Siehe oben: FEHLER: Balkenquerschnitt ist in Bauteil nicht definiert.
FEHLER: Ungleiche Klammern in ergebnisbasierter Lastkurve gefunden: Funktion.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Die Syntax der Gleichung für den Suchlaufwert hat ein Problem mit der Gruppierung der Klammern ( ). Überprüfen Sie die Gleichung auf Genauigkeit und korrigieren Sie sie.
FEHLER: Unbekannte Eingabe in ergebnisbasierter Lastkurve: Funktion.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Die Gleichung für den Suchlaufwert enthält nicht erkannten Text. Überprüfen Sie die Gleichung, und vergleichen Sie sie mit der oben angegebenen Tabelle der zulässigen Operatoren und Funktionen.
FEHLER: Unbekannter Operator in ergebnisbasierter Lastkurve: Funktion.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Die Gleichung für den Suchlaufwert enthält nicht erkannten Text. Überprüfen Sie die Gleichung, und vergleichen Sie sie mit der oben angegebenen Tabelle der zulässigen Operatoren und Funktionen.
FEHLER: Unbekannte Variable in ergebnisbasierter Lastkurve.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Die Gleichung für den Suchlaufwert enthält nicht erkannten Text. Jede Variable in der Gleichung muss in der Variablen-Tabellenkalkulation definiert sein. Überprüfen Sie die Gleichung auf Genauigkeit und korrigieren Sie sie erforderlichenfalls.
Fehler: Verwendung inkompatibler Modi in einem Modell mit linearen und nichtlinearen Elementbauteilen
Ursache: Verschiedene Eingaben können dazu führen, dass ein Bauteil durch den Prozessor sowohl als linear als auch als nichtlinear behandelt wird. (Zu den Einstellungen, die diese Auswirkung haben können, gehören Druckbelastung, die Analyseart Kleine Verschiebungen oder Große Verschiebungen im Dialogfeld Elementdefinition, das Materialmodell usw.) Diese Fehlermeldung weist darauf hin, dass der Prozessor das Modell nicht auflösen kann, da einige Bauteile linear und einige nichtlinear sind.
Aktion: Lösungen für das Problem sind Folgende:
  1. Legen Sie die Analyseart aller Bauteile auf die gleiche Auswahl fest, also entweder Kleine Verschiebungen oder Große Verschiebungen. (Elementdefinition, Registerkarte Allgemein)
  2. Lassen Sie die Analyseart wie festgelegt, ändern Sie jedoch die Kompatibilität zu Erzwingen für alle Bauteile. (Elementdefinition, Registerkarte Erweitert.)
Keine positive Diagonale!
Ursache: Die Steifigkeitsmatrix enthält einen Wert Null auf der Diagonalen. Solche Matrizen können nicht gelöst werden und weisen auf ein Problem bei der Einrichtung des Modells hin.
Aktion: Prüfen Sie für nicht lineare statische Spannungsanalyse, dass jede Unterbaugruppe im Modell in allen Richtungen eingeschränkt ist. Bei Kontaktmodellen müssen ggf. künstliche Federn hinzugefügt werden, um in den Iterationen, in denen die Bauteile nicht in Kontakt sind, Stabilität zu geben. (Die Bauteile sollten zwar theoretisch in Kontakt sein, die Gleichgewichtsiterationen können aber an einen Punkt gelangen, an dem sich die Bauteile nicht in Kontakt befinden.) Prüfen Sie für die MES-Analyse, dass jede Unterbaugruppe eine Masse (für die Translationssteifigkeit) und Trägheitsmoment um Drehachsen (für die Drehsteifigkeit) hat. Überprüfen Sie die Materialeigenschaften (sowohl im FEM-Editor als auch in der Analyseübersichtsdatei), um zu bestätigen, dass alle Eigenschaften eingegeben wurden.
Anmerkung: Die Iterationsmethode wurde zu Volles Newton ohne Zeilensuche geändert, da Große Festkörperrotation für Bauteil N ausgewählt ist.
Wenn für ein Balkenelement die Option Große Festkörperrotation aktiviert ist, muss der Prozessor die iterative Lösungsmethode Volles Newton ohne Zeilensuche verwenden. Dieser Hinweis gibt an, dass der Prozessor zu diesem Gleichungslöser aufgrund des Wechsels bei der Festkörperrotation gewechselt ist. Weiter ist keine Aktion erforderlich. Weitere Informationen finden Sie unter Erweiterte Parameter für Balkenelemente auf der Seite Balkenelemente.
Autotm-Grenze erreicht.
Ursache: Die Analyse hat den Zeitschritt 18 Mal verringert (L=19) und ist nicht konvergiert. Da der Zeitschritt jetzt sehr klein ist, ist es wahrscheinlich, dass das Modell Stabilitätsprobleme hat.
Aktion: Wenn die Zeitschrittstufe direkt von 1 zu 19 geht, dann fehlt dem Modell Steifigkeit. Nachfolgend sind einige allgemeine Probleme aufgeführt, die zu Steifigkeitsproblemen führen:
  • Eine nichtlineare statische Analyse, in der das Modell nicht statisch stabil ist.
  • In vollständigen Analysen im Mechanischen Ereignissimulator können Steifigkeitsprobleme auftreten, wenn ein Bauteil keine Masse hat und nicht statisch stabil ist. (Ohne Masse oder Steifigkeit kann das Bauteil sich bei jeder Kraft in einem unendlichen Abstand bewegen.)
  • Wenn das Modell Dichtungselemente enthält, prüfen Sie, ob die oberen und unteren Flächen der Dichtung definiert wurden. (Weitere Informationen finden Sie im Absatz Grundlegende Schritte für die Verwendung von 3D-Dichtungselementen auf der Seite 3D-Dichtungselemente.)
Wenn das Modell eine Zeitlang konvergiert, dann aber die Zeitschrittstufe L auf L=19 abfällt, dann ist es möglich, dass das Modell instabil oder zu steif geworden ist. Wenn zum Beispiel das Materialmodell für armierten Beton verwendet wird, hat möglicherweise der Betonquerschnitt vollständig versagt; prüfen Sie den Fehlerstatus in der Ergebnisanzeige. Aufgrund der großen Verformungseffekte ist das Modell vielleicht von einem stabilen Zustand in einen instabilen Zustand (wie Durchbrechen oder Beulen) übergegangen.
Bei einem Fläche-zu-Fläche-Kontakt kann der Zeitschritt zum Kontaktzeitpunkt auf einen geringen Wert reduziert werden (L auf einen großen Wert erhöht), wenn die Kontaktsteifigkeit zu groß ist. Der Prozessor verringert dann den Zeitschritt von keiner Steifigkeit vor dem Kontakt zu großer Steifigkeit direkt nach dem Kontakt.
Wenn die Analyse langsam konvergiert und das Modell Brickelemente enthält, dann bestehen die beiden Optionen, ein gröberes Quadernetz zu verwenden oder das Netz zu einem Tetraedernetz zu ändern. (Bei beiden Optionen muss das Modell neu vernetzt werden.) Das Ziel besteht in der Verbesserung der Form der Elemente, was zu einer Verbesserung der Konvergenz führen kann. Ggf. muss daher nur die Netzqualität einiger bestimmter Bauteile verbessert werden. Wenn auch das Problem ernsthaft genug sein kann, um eine Warnung über ein verzerrtes Element zu generieren, können die Methoden auf der Seite Kraftschlüssige Jacobimatrix-Fehler oder verformte Elemente auch zum Prüfen und Verbessern der Netzqualität in dieser Situation verwendet werden. Beachten Sie, dass die Volumenkörpernetzstatistik, die auf dieser Seite beschrieben wird, sich auf die unverformte Form bezieht; die Verformung, die während der Analyse auftritt, kann zu zusätzlicher Verzerrung führen.
STOPP: nichtlineare Bauteilnummer überschritten
Ursache: Verschiedene Eingaben können dazu führen, dass ein Bauteil durch den Prozessor sowohl als linear als auch als nichtlinear behandelt wird. (Zu den Einstellungen, die diese Auswirkung haben können, gehören Druckbelastung, die Analyseart Kleine Verschiebungen oder Große Verschiebungen im Dialogfeld Elementdefinition, das Materialmodell usw.) Diese Fehlermeldung weist darauf hin, dass der Prozessor das Modell nicht auflösen kann, da einige Bauteile linear und einige nichtlinear sind.
Aktion: Lösungen für das Problem sind Folgende:
  1. Legen Sie die Analyseart aller Bauteile auf die gleiche Auswahl fest, also entweder Kleine Verschiebungen oder Große Verschiebungen. (Elementdefinition, Registerkarte Allgemein)
  2. Lassen Sie die Analyseart wie festgelegt, ändern Sie jedoch die Kompatibilität zu Erzwingen für alle Bauteile. (Elementdefinition, Registerkarte Erweitert.)
Stopp: Temperatur außerhalb des Eingabebereichs für Materialeigenschafttemperaturen!
Gefundene Temperatur = T
Sollte innerhalb des Bereichs liegen: (Tmin Tmax)
Ursache: Das Materialmodell für ein Bauteil ist für die Verwendung von temperaturabhängigen Materialeigenschaften festgelegt. Eine berechnete Temperatur T liegt jedoch nicht im Temperaturbereich (Tmin bis Tmax), der in den Materialeigenschaften eingegeben wurde. Da der Prozessor die Materialeigenschaften nicht extrapoliert, kann die Analyse nicht fortgesetzt werden.
Aktion: Das Problem mit diesen Fehler ist, dass die berechnete Temperatur T häufig nicht mit den vom Benutzer eingegebenen Temperaturen zusammenzuhängen scheint, vor allem, wenn Mittelknoten verwendet werden. Dies liegt am Verhalten von FEM. Die berechneten Temperaturen T liegen bei den Integrationspunkten, und aus theoretischen Gründen liegen diese Temperaturen häufig nicht zwischen den Temperaturen an den Knoten. So können z. B. Temperaturen von 60, 40 und 70 am Eckknoten, versetzten Mittelknoten und der entgegengesetzten Ecke theoretisch zu Temperaturen von 35 an den Integrationspunkten führen, und dies ist die Temperatur, für die keine Materialeigenschaften vorliegen. Überprüfen Sie die folgenden Objekte im Modell:
  1. Vergewissern Sie sich, dass die Temperaturen an allen Knoten definiert wurden (einschließlich der Mittelknoten, falls zutreffend) und akzeptabel sind.
  2. Erweitern Sie die Materialeigenschaften über den Bereich der Eingabetemperaturen hinaus, um die intern berechneten Temperaturen abzudecken. Das Erweitern der Materialeigenschaften und Wiederholen der Analyse kann das Problem lösen, das beim ersten Lauf auftrat, doch es kann ein anderes Element vorliegen, bei dem die interne Temperatur weiter außerhalb des erwarteten Bereichs liegt, was zur gleichen Fehlermeldung mit einer anderen berechneten Temperatur T führt.

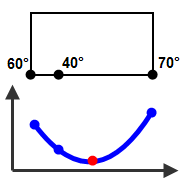
    Die Interpolation der Temperaturkurve (blaue Punkte) ergibt ein Minimum (roter Punkt), das kleiner als alle benutzerdefinierten Temperaturen ist.

STOPP: Betonmaterialkonstanten (C0,A1,A2,A3) können aus den angegebenen Betonstärken nicht bestimmt werden. Prüfen Sie die Eingaben oder geben Sie Materialkonstanten direkt ein. Elementgruppennummer = X
Ursache: Die für den armierten Beton eingegebenen Materialeigenschaften wurden zum Berechnen der Fehlerparameter verwendet (C0, A1, A2, A3), doch die Lösung für die Gleichungen für diese Parameter konnte nicht gefunden werden. (Die Bauteil- oder die Gruppennummer wird in der Fehlermeldung angegeben.)
Aktion: Da diese Parameter anhand der Stärken berechnet werden, die auf der Registerkarte Stärken der Materialeigenschaften eingegeben wurden, überprüfen Sie, dass die Stärken richtig eingegeben wurden.
Wenn die Parameter bekannt sind, können sie auch direkt in den Materialeigenschaften eingegeben werden (Registerkarte Erweitert), anstatt sie vom Prozessor berechnen zu lassen. Anweisungen zum Ableiten der Konstanten aus den Testdaten finden Sie auf der Seite Armierter Beton - Theoretische Beschreibung. Auch wenn die Parameter nicht bekannt sind, kann der Versuch, sie zu berechnen, möglicherweise klären, weshalt sie nicht vom Prozessor berechnet werden können. Welche Eingabe ist das Problem?
Zeitschrittreduzierung aufgrund von: tttt
Wenn die Gleichgewichtsiterationen konvergieren, gibt der Buchstabe c nach der Restzahl die Konvergenz an. Nach diesem Punkt in der Lösung werden andere Kriterien überprüft, um festzustellen, ob sie die Konvergenz erfüllen. Wenn irgend einer dieser weiteren Faktoren verletzt wird, dann wird für den zuerst gefundenen Fehler diese Meldung mit der Erläuterung (tttt) ausgegeben, z. B. Zeitschrittreduzierung aufgrund von: Kontaktdurchdringung.
Warnung: Bedingung in der ergebnisbasierten Lastkurve ist nicht in der Datenbank angegeben.
Fehler bei einer ergebnisbasierten Last (siehe Tipp unten). Der Bedingungstext in den Analysenparametern enthält Suchlaufwerte, die nicht definiert wurden. Überprüfen Sie die Bedingung auf Genauigkeit und korrigieren Sie sie, oder definieren Sie die Variablen, die im Bedingungstext verwendet werden. Der Bedingungstext kann auch leer sein, was akzeptabel ist und kein Problem darstellt.
Warnung: verformtes Element N in Bauteil P, behält Integrität bei!
Wenn ein Element stark verformt ist, sodass die Determinante des Elements kleiner als 0 ist, kann die Lösung nicht gefunden werden. Theoretisch sollte die Analyse anhalten. Die Warnung kann aber während einer Zwischeniteration auftreten, und in einer späteren Iteration kann es zu einer Wiederherstellung kommen. Die letzte Iteration, bei der der Zeitschritt konvergiert, enthält möglicherweise begrenzte Elementverzerrung und kann daher akzeptabel sein. Diese Warnmeldung weist auf folgendes Szenario hin: Die Elementnummer N in Bauteilnummer P war verformt. Zum Fortsetzen der Analyse wurde die Steifigkeit angepasst, um eine Lösung zu erhalten.
Anmerkungen:
  • Die Vorgabemethode für eine übermäßige Elementverzerrung besteht in der Reduktion des Zeitschritts. Dieser Fehler wird nur dann angezeigt, wenn die Option Bei verzerrten Elementen Zeitschrittreduzierung deaktiviert ist. Diese Option ist auf der Registerkarte Zeitschritt im Dialogfeld Analyseparameter Erweitert.
  • Die Anzahl der Warnungen pro Zeitschritt (nicht pro Iteration) kann begrenzt werden. Je nach den Einstellungen zeigt die Protokolldatei möglicherweise nicht an, ob Warnungen während der letzten Iteration aufgetreten sind, bei der der Zeitschritt konvergierte. Weitere Informationen finden Sie unter Steuern der Ausgabedateien.
Warnung: angetriebener Knoten der Scheibe (Bauteilnr.: n) hat die Scheibe erreicht.
Warnung: treibender Knoten der Scheibe (Bauteilnr.: n) hat die Scheibe erreicht.
Ursache: Ein Knoten auf der Scheibe n (entweder Totpunkt oder Antrieb) hat sich soweit bewegt, dass er nun die Scheibe berührt. Wenn der Knoten sich weiterhin in Richtung der Scheibe bewegt, verletzt die Mathematik die physikalische Realität. Die Elemente, die mit dem Scheibenelement verbunden sind, gehen durch den Körper der Scheibe.
Aktion: Definieren Sie die Scheibe neu, und verschieben Sie die Endknoten weiter weg.
Warnung: Fehlendes Dehnungsverfestigungsmodul für Material, ID = n
Ursache: Ein Kunststoffmaterialmodell wurde für Bauteil n festgelegt, aber in den Materialeigenschaften fehlen einige Daten zur Berechnung des Dehnungsverfestigungsmoduls.
Aktion: Bearbeiten Sie die Materialeigenschaften für Bauteil n, und geben Sie die fehlenden Daten ein. Weitere Informationen finden Sie auf der Seite von Mises-Materialeigenschaften.
Warnung: Knotenkoordinate ist kleiner als die global definierte Koordinate der unteren Begrenzungswand
Eine Aufprallfläche ist im Modell vorhanden, und die angegebenen Knoten liegen unterhalb der Aufprallfläche. Verwenden Sie die Ergebnisanzeige zum Suchen der referenzierten Knotennummer (Abfragen: Ergebnisse: Angeben), und korrigieren Sie dann die Position der Aufprallfläche bzw. des Modells, wenn die Warnung kritisch ist. Wenn der Knoten für die Bewegung nicht entscheidend ist, wie z. B. der K-Knoten eines Balkens (in der Regel eine sehr große Koordinate), dann hat die Warnung keine Bedeutung.
WARNUNG! Nichtpositive Hauptstreckung gefunden.
Diese Meldung gibt an, dass eine negative Hauptstreckung in einem hyperelastischen Materialmodell gefunden wurde, und dass der Hauptstreckungswert auf 1 gesetzt wird, um die Integrität des Elements zu erhalten. Negative Hauptstreckungen treten auf, wenn eine starke Verzerrung dazu führt, dass der Jacobi-Wert des Elements negativ wird.
Warnung: Wenn in der Analyse ein (allgemeines) Kontaktelement verwendet wird, wird <MES mit nichtlinearen Materialmodellen> empfohlen.
Ursache: Die Analyse ist auf Statische Spannung mit nichtlinearen Materialmodellen festgelegt und enthält den Elementtyp Kontakt oder Allgemeiner Kontakt. Die Konvergenz dieser Kombinationen kann langsam sein.
Aktion: Stellen Sie zunächst sicher, dass alle Bauteile des Modells statisch stabil sind, ohne die Kontaktelemente zu verwenden. Da nicht garantiert werden kann, dass die Kontaktelemente bei jeder Iteration verwendet werden, ist das Modell möglicherweise nicht in allen Iterationen statisch stabil. Wenn dies der Fall ist, kann die Analyse anhalten oder langsam konvergieren. Fügen Sie ggf. Begrenzungsbedingungen und schwache Federelemente hinzu, um das Modell zu stabilisieren.
Zweitens kann der Wechsel der Analyseart zu Mechanischer Ereignissimulator (MES) zu besserer Konvergenz führen. Da MES die Trägheit der Bauteile berechnet, können sie sich in einem Zeitschrit nicht unendlich bewegen (vorausgesetzt, die Bauteile haben Masse).
Warnung: Wenn ein (allgemeines) Kontaktelement in der Analyse verwendet wird, wird die Lösungsmethode <Volles Newton mit Zeilensuche> empfohlen.
Ursache: Die Analyse enthält den Elementtyp Kontakt oder Allgemeiner Kontakt, und die nichtlineare iterative Lösungsmethode ist nicht auf Volles Newton mit Zeilensuche festgelegt. Die Konvergenz dieser Situationen kann langsam sein.
Aktion: Ändern Sie Analysenparameter: Erweitert: Gleichgewicht: Nichtlineare iterative Lösungsmethode entweder zu Automatisch oder zu Volles Newton mit Zeilensuche. Bei Festlegen von Automatisch wählt der Prozessor die beste Lösungsmethode.

Themen in diesem Abschnitt
Übergeordnetes Thema: Nichtlineare Analysen