Характеристики Модального, Сейсмического и Сейсмического псевдомодального методов расчета конструкции представлены ниже.
Модальный расчет
Модальный расчет конструкции позволяет установить первые n собственных значений и собственных векторов конструкции.
Доступные методы расчета: метод итераций в подпространствах, метод Ланцоша и метод редукции базиса.
Итерации будут завершены, когда будет выполнено следующее условие:
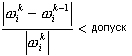
где, i = 1,2,…,n - формы колебаний, k – число итераций.
Верхний предел – это значение периода (круговой частоты, частоты), определяющее диапазон (0, верхний предел) , в котором будут найдены собственные значения и собственные вектора.
Для этого типа расчета конструкции возможна проверка Штурма, которая позволяет находить пропущенные собственные значения.
2. Сейсмический расчет
Для сейсмического и спектрального расчетов конструкции нет необходимости определять упорядоченную систему собственных значений и собственных векторов. Для этих типов расчета важны только те n собственных значений и собственных векторов конструкции, которые характеризуются большим коэффициентом участия масс.
Эти значения не должны быть упорядочены, некоторые собственные значения и собственные вектора могут быть проигнорированы.
Доступные методы анализа: метод Ланцоша.
Метод сходимости:
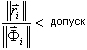
где,
Φ i - i-й собственный вектор
Верхний предел: предельные значения игнорируются.
Для этого типа расчета проверка Штурма не выполняется.
Сейсмический псевдомодальный расчет
Этот режим используется только при спектральном и сейсмическом расчетах. Он должен использоваться в случае, если классические методы расчета, основанные на модальной декомпозиции, приводят к очень длительному расчету. Этот метод состоит в представлении вектора X в виде суперпозиции определенных основных векторов, которые не являются точным приближением формы Φ i .
Доступные методы анализа: метод Ланцоша.
Для этого типа расчета проверка Штурма не выполняется.
Если выбран метод Ланцоша, метод вычислений в программе изменяется на метод итераций в подпространствах. Тем не менее, если требуется использовать в расчетах метод Ланцоша, то разделенные конструкции должны быть связаны таким образом, чтобы модель конструкции была неизменна (например, должен быть добавлен стержень на опорах).