二维单元是必须在整体 Y-Z 平面中输入的 3 节点或 4 节点等参三角形或四边形。图 1 显示了一些典型的二维单元。如图 2 中所示,该单元可以表示平面或轴对称实体。在这两种情况下,每个单元节点均有两个平动自由度。如果该单元用于表示轴对称实体或壳,则整体 Z 轴为旋转轴。所有单元均必须位于以 Y 为半径轴的 +Y 半平面中。图 2 说明了这些约定。
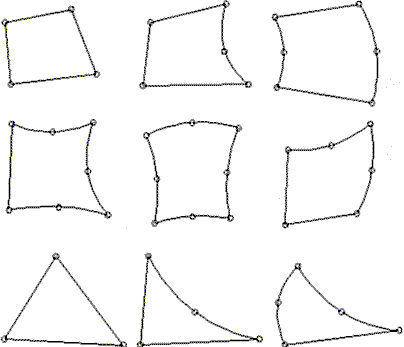
图 1:二维单元的节点配置
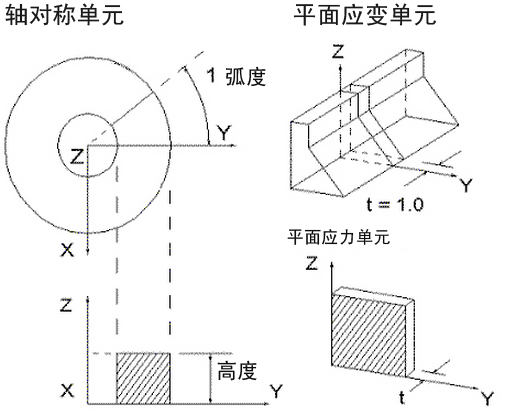
图 2:二维单元的应用
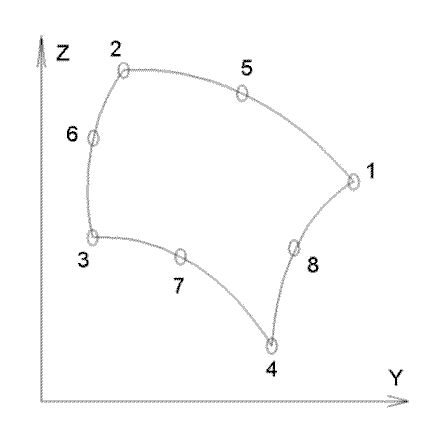
图 3:二维单元示例
选择二维单元的类型
有三种类型的二维单元可用于非线性分析。可以在“单元定义”对话框“常规”选项卡上的“几何类型”下拉框中选择这些单元。
- 轴对称:对于使用围绕 Z 轴的几何、载荷和边界条件对称来对实体进行建模的单元,请选择此几何类型。Y 坐标不得为负。如果节点倾向旋转轴(Z 轴),则必须约束 Y 方向上的平动。使用圆中的弧度数(载荷除以弧度)标准化节点载荷。

图 1:二维轴对称模型
- “平面应变”:选择此几何类型可创建实体模型(不显示垂直于 YZ 平面的变形)。由于假定 X 方向上没有变形,因此该分析假定厚度为 1 个单位;您可以输入厚度,但此厚度仅用于“结果”环境中的三维可视化。所有输入载荷和结果均基于 1 个单位的厚度。
图 2:二维平面应变
- 平面应力:选择此几何类型可创建指定厚度垂直于 YZ 平面的实体模型(不显示垂直于 YZ 平面的应力)。您可修改本构关系,使应力垂直于 YZ 平面零。所有载荷沿厚度均匀分布。
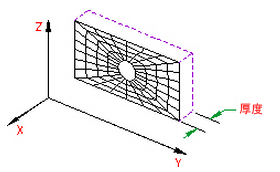
图 3:二维平面应力模型
二维单元参数
首先,从“单元定义”对话框“常规”选项卡上的列表框中指定“材料模型”。许多附加输入参数取决于选定材料模型。可用的材料模型分为以下几类。(有关各个材料模型的详细信息,请参考材料属性页面下的相应页面。)
-
弹性
- “各向同性”:此材料模型选项用于那些仅在应力-应变曲线的弹性区域中出现变形的部件。若要使用此材料模型,这些部件必须在所有方向具有相同的材料属性。单个弹性模量和泊松比将是所需的材料属性。
- “正交各向异性”:此材料模型选项用于那些仅在应力-应变曲线的弹性区域中出现变形的部件。部件可能在特定的方向具有不同的材料属性。具体而言,材料属性可能在直角坐标系的一个或三个正交方向上均存在差异。
- “可变切线”:此材料模型选项用于地质材料分析。此模型描述了各向同性材料,该类材料的体积模量和剪切模量是应力和应变不变量的函数。
- “曲线”:此材料模型选项也用于地质材料分析。在此模型中,瞬时体积模量和剪切模量由当前体积应变的分段线性函数定义。
- “含截止的曲线”:此材料模型选项类似于上述曲线材料模型,但不同的是,在分析某些问题时,所施载荷产生的拉伸应力不可以超过重力压力。在这种情况下,可使用此材料模型来模拟拉伸截止,例如,该材料模型可表示在拉伸应力超过重力压力值时,拉伸应力方向上刚度的降低情况。
- “温度相关各向同性”:此材料模型用于对那些不仅在应力-应变曲线的弹性区域出现变形、而且由于温差而产生应力的材料进行建模。
- “Duncan-Chang 土体”:Duncan-Chang (1970) 模型用于模拟土体。它基于三轴土体测试并假设存在应力/应变双曲线关系。使用此材料模型时,“几何类型”不能为“平面应力”,并且需要将“高级”选项卡上的“分析公式”设置为“仅材料非线性”。
-
超弹性
- Mooney-Rivlin:此材料模型用于对橡胶等超弹性材料进行建模。
- Arruda-Boyce:此材料模型是用于对橡胶材料进行建模的超弹性材料模型。该材料模型符合体积守恒变形模式下的 Ogden 材料性能。
- Ogden:此材料模型用于对橡胶等超弹性材料进行建模。
- Yeoh:此材料模型用于对橡胶等近似不可压缩(体积守恒)的超弹性材料进行建模。仅可使用“完全拉格朗日”分析公式。
- Neo-Hookean:此材料模型用于对橡胶等近似不可压缩(体积守恒)的超弹性材料进行建模。仅可使用“完全拉格朗日”分析公式。
- Van der Waals:此材料模型用于对橡胶等近似不可压缩(体积守恒)的超弹性材料进行建模。仅可使用“完全拉格朗日”分析公式。
-
泡沫
- Blatz-Ko:此材料模型涉及体积部件与非体积部件之间的强耦合,如体积模量,而体积模量不可以单独确定,这一点与其他超弹性材料模型不同。
- 超弹泡沫:此材料模型用于超弹性材料,这与 Ogden 材料模型类似。此材料模型用于表示材料的可压缩性。这不适用于平面应变单元。
-
粘弹性
- 粘弹性 Mooney-Rivlin:Mooney-Rivlin(超弹性)材料模型的粘弹性变化。
- 热蠕变粘弹性:此材料模型用于对那些不仅在应力-应变曲线的弹性区域中发生变形、而且出现蠕变的材料进行建模。模型在恒定载荷作用一段时间后发生变形的现象即蠕变。有关设置用于此材料模型的蠕变定律的信息,请参见“定义二维单元的热属性”段落。
- 粘弹性 Arruda-Boyce:Arruda-Boyce(超弹性)材料模型的粘弹性变化。
- 粘弹性 Blatz-Ko:Blatz-Ko (超弹泡沫)材料模型的粘弹性变化。
- 粘弹性 Ogden:Ogden(超弹性)材料模型的粘弹性变化。
- 粘弹性超弹泡沫:超弹泡沫材料模型的粘弹性变化。
- 线性粘弹性各向同性:这是一种材料呈现出弹性实体和粘性流体属性的粘弹性材料模型。粘弹性属性基于 Prony 序列。这些属性在所有方向上均相同(各向同性)且与温度无关。
- 线性粘弹性正交各向异性:这是一种材料呈现出弹性实体和粘性流体属性的粘弹性材料模型。粘弹性属性基于 Prony 序列。这些属性在三个垂直方向上不同(正交各向异性)且与温度无关。
- 线性热粘弹性各向同性:这是一种材料呈现出弹性实体和粘性流体属性的粘弹性材料模型。粘弹性属性基于 Prony 序列。这些属性在所有方向上均相同(各向同性)且与温度相关。
- 粘弹性 Neo-Hookean:这是 Neo-Hookean(超弹性)材料模型的粘弹性变化。
- 粘弹性 Yeoh:这是 Yeoh(超弹性)材料模型的粘弹性变化。
- 粘弹性 Van der Waals:这是 Van der Waals(超弹性)材料模型的粘弹性变化。
-
塑性
- von mises 多线性等向强化:此材料模型选项用于那些可能会在分析过程中发生塑性变形的部件。您需定义双线性曲线来控制应力-应变关系。
- von mises 双线性随动强化:此材料模型选项也用于那些可能会在分析过程中发生塑性变形的部件。您需定义双线性曲线来控制应力-应变关系。当模型承受循环载荷时,应首选此材料模型选项,而不是“von mises 多线性等向强化”材料模型选项
- von mises 多线性等向强化:此材料模型选项用于那些可能会在分析过程中发生塑性变形的部件。您将能够使用多个数据点指定应力-应变曲线来控制应力-应变关系。
- von mises 多线性随动强化:此材料模型选项用于那些可能会在分析过程中发生塑性变形的部件。您将能够使用多个数据点指定应力-应变曲线来控制应力-应变关系。当模型承受循环载荷(包辛格效应)时,应首选此材料模型选项,而不是“von mises 多线性等向强化”材料模型选项。
- 温度相关塑性:此材料模型用于对那些不仅在分析过程中发生塑性变形、而且由于温差而产生应力的材料进行建模。
-
粘塑性
- 热蠕变粘塑性:此材料模型用于对那些发生塑性变形和蠕变的材料进行建模。模型在恒定载荷作用一段时间后发生变形的现象即蠕变。有关设置用于此材料模型的蠕变定律的信息,请参见“定义二维单元的热属性”段落。
- Drucker-Prager:此材料模型类似于 von mises 材料模型,但增加了屈服函数。该模型假设屈服函数受体积应变影响。这种情况可在混凝土和岩石等材料中出现。
几何类型:使用“几何类型”下拉框指定几何类型。如果使用平面应力或平面应变几何类型,则必须在“单元定义”对话框的“厚度”字段中定义部件的厚度。
对于此部件中要激活中节点的二维单元,请在“中节点”下拉框中选择“包括”选项。选择此选项后,二维单元将在每条边的中点处定义更多节点。这会将 4 节点二维单元更改为 8 节点二维单元。带有中节点的单元有助于更精确地计算梯度。但是,带有中节点的单元会增加处理时间。若网格足够小,则中节点无法显著提高精确度。
使用“分析类型”下拉菜单,可设置预期的位移类型。“小位移”适用于未发生运动且应变较小的部件,并将忽略因大变形而产生的非线性几何效应。(它还会将“高级”选项卡上的“分析公式”设置为“仅材料非线性”。)“大位移”适用于发生运动和/或大应变的部件。(还应根据分析需要设置“高级”选项卡上的“分析公式”。)
- 系统始终输出中节点处的位移。仅当用户在运行分析之前激活该选项以输出这些结果时,系统才会输出中节点处的应力和应变。该选项位于“输出”选项卡上的“设置”
 “模型设置”
“模型设置” “参数”
“参数” “高级”对话框下。(有关详细信息,请参见控制输出文件页面。)
“高级”对话框下。(有关详细信息,请参见控制输出文件页面。) - 使用

 “选项”
“选项” “分析”选项卡,并设置“使用大位移作为非线性分析默认值”选项,控制“分析类型”是默认为小位移还是大位移。
“分析”选项卡,并设置“使用大位移作为非线性分析默认值”选项,控制“分析类型”是默认为小位移还是大位移。
控制二维单元的方向
二维单元有两组轴:单元轴和材料轴。在此段落中,单元轴指定为 Elem1 和 Elem2,而材料轴指定为 Mat1 和 Mat2。该文档的其他部分可能称之为轴 1 和轴 2。
对于常规的 FEA 分析,您可以忽略单元方向(Elem1 和 Elem2)。能够定位单元,这对采用正交各向异性材料模型的单元非常有用。可在“单元定义”对话框的“方向”选项卡中完成此操作。“方法”下拉框包含三个选项,可用于指定单元的哪一边为 ij 边。如果选择“默认”选项,则具有最大表面编号的单元边将选择作为 ij 边。如果选择“定位 I 节点”选项,则必须在“Y 坐标”和“Z 坐标”字段中定义坐标。单元上最靠近此点的节点将指定为 i 节点。j 节点将是单元上下一个逆时针旋转的节点(+X 轴的右手法则)。如果选择“定位 IJ 边”选项,则必须在“Y 坐标”和“Z 坐标”字段中定义坐标。单元上最靠近此点的边将指定为 ij 边。i 和 j 节点均会指定,以便沿单元从 i 节点逆时针旋转达到 j 节点。
一旦确定 ij 边,系统会将单元轴 Elem1 设置为平行于 ij 边。绕 X 轴顺时针旋转 90 度即可得到轴 Elem2。请参见图 1。
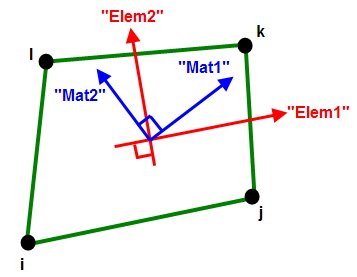
图 1:单元轴和材料轴
单元轴 Elem1 平行于单元的 ij 边。
材料轴 Mat1 可从单元轴偏移。
“材料轴方向”:当二维单元使用正交各向异性材料模型时,请定义三条材料轴。材料轴 Mat1 和 Mat2 位于单元的平面中,Mat3 平行于 X 轴。
在“单元定义”对话框的“常规”选项卡中,可以使用两种方法定义材料轴。第一种是使用“Y 方向”和“Z 方向”字段定义矢量。材料轴 1 平行于总体矢量。材料轴 2 将是 X 轴与材料轴 1 的叉积。图 2 和 3 阐述了此方法。如果未在“Y 方向”或“Z 方向”字段中指定值,则“材料轴转动角度”字段中的值将用于定位相对于单元轴 Elem1 的材料轴。如果将部件从原始片体压模制成具体形状,这非常有用。转动角度 β 对应于材料轴 1 相对于每个单元的单元轴 1 的角度。请参见图 4。
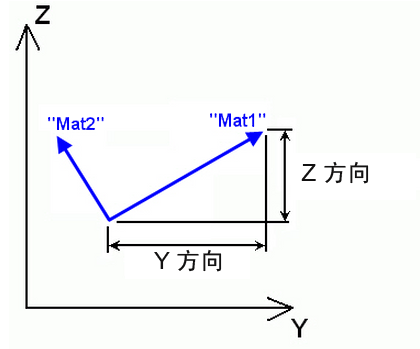
图 2:材料轴方向的 Y 和 Z 方向定义
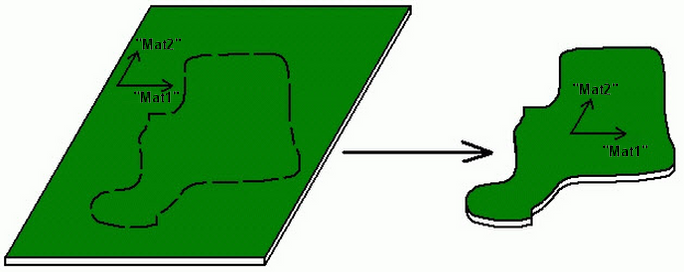
图 3:剪自正交各向异性材料的部件
尽管网格具有随机性,从而生成随机的单元轴,但材料轴是一致的。

图 4:材料轴方向的转动角度定义
定义二维单元的热属性
“热”部分:
如果二维单元部件使用具有热效应的材料模型,则必须在“单元定义”对话框“热”选项卡上的“无应力参考温度”字段中指定一个值。此值将用作参考温度,使用节点温度的双线性插值计算与热增长约束关联的、基于单元的载荷。
“蠕变”部分:
如果二维单元部件使用包含蠕变的材料模型,请在“蠕变定律”下拉框中选择该选项。此选项将用于计算分析过程中的蠕变效应。可用的蠕变定律如下:
- 无蠕变:选择此选项后,分析中不包含蠕变效应。
- 幂律:此选项也称为“单轴蠕变定律”。方程为
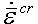 = C
1
x
= C
1
x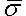 C2
x t
C3
。
C2
x t
C3
。 - Garofalo:此选项也称为“双曲正弦蠕变定律”。方程为
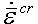 = A
0
x [sinh(A
1
x
= A
0
x [sinh(A
1
x 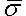 )]
A2
。
)]
A2
。 - 双幂率:此选项类似于幂律,但是增加了一项,可在高应力条件下生成更接近实验结果的结果。方程为
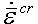 = C
1
x
= C
1
x 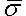 C
2
x t
C3
+ C
4
x
C
2
x t
C3
+ C
4
x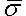 C5
x t
C6
。
C5
x t
C6
。
其中,![]() 是有效的蠕变应变率,
是有效的蠕变应变率,![]() 是有效应力。有关输入材料属性的重要信息,另请参考热蠕变粘弹性材料属性页面。
是有效应力。有关输入材料属性的重要信息,另请参考热蠕变粘弹性材料属性页面。
若要根据尺寸均匀的时间步分区计算蠕变,请在“时间积分方法”下拉框中选择“固定子步”选项。若要根据尺寸可变的时间步分区计算蠕变,请选择“可变子步”选项。这两种方法均基于时间硬化,并使用显式时间积分方法。在某些载荷条件下,这些方法可能会变得不稳定。使用“热蠕变粘弹性”材料模型时,“时间积分方法”下拉框中将提供一个附加选项:“Alpha 方法”。此方法使用隐式时间积分方案改善蠕变行为,且无条件稳定。
在“无应力参考温度”字段中,指定不存在热应力时的温度。
“蠕变应变定义”下拉框中的“有效的”选项适用于非循环载荷分析。
在分析期间,将蠕变计算作为每个时间步的子步迭代执行。可以在“最大子步数”字段中控制单个时间步允许的子步数。此外,还可以在“子步中的最大迭代次数”字段中指定单个子步可执行的迭代次数。在每次子步迭代后,将蠕变应力和应变与上一次迭代进行比较。如果该值超出在“蠕变应变计算容差”和“蠕变应力计算容差”字段中指定的容差,则需要执行另一次迭代。
使用“Alpha 方法”作为“时间积分”方法时,需要指定“时间积分参数”。若要对时间积分方案使用全显式方法(但是不同于固定/可变子步的显式方法),请在“时间积分参数”字段中键入 0.0。若要使用全隐式方法,请在“时间积分参数”字段中键入 1.0。当“时间积分参数”大于 0.5 时,此方法无条件稳定。
高级二维单元参数
在“高级”选项卡的“分析公式”下拉框中,选择要用于二维单元的公式方法。
- 如果选择“仅材料非线性”选项,则将考虑非线性材料模型效应,但是基于未变形几何体执行所有计算。因此,此公式适用于应变较小且没有运动的部件。如果将“常规”选项卡上的“分析类型”设置为“小位移”,这将是唯一可用的选项。
- “完全拉格朗日”选项中的所有静态变量和运动变量均参考模型的初始未变形配置。此公式适用于发生运动且应变较小的部件。请注意,材料属性应与工程应力和应变相关。
- “更新拉格朗日”中的所有静态变量和运动变量均参考模型的最后计算配置。此公式适用于发生运动且应变较大的部件。请注意,材料属性应该与实际应力和应变相关。
接下来,在“积分阶次”下拉框中选择将对此部件中的二维单元使用的积分阶次。对于矩形单元,请选择“2 阶”选项。对于中度扭曲的单元,请选择“3 阶”选项。对于极度扭曲的单元,请选择“4 阶”选项。单元刚度公式的计算时间将以积分阶次的三次方增加。因此,为缩短处理时间,应使用将生成可接受结果的最低积分阶次。
如果将材料模型(在“常规”选项卡中)设置为以下塑性材料模型之一,则使用“应力更新方法”:
- von mises 多线性等向强化
- von mises 双线性随动强化
- von mises 多线性等向强化
- von mises 多线性等向强化
在材料趋于塑性时,此选项可控制用于求本构方程积分的数值算法(应力/应变定律)。适用于“应力更新方法”的选项如下:
- “显式”:(原始方法)。此选项使用显式子增量 Forward Euler 方法求本构方程的积分。“显式”选项最适合于简单问题(如简单拉伸),因为该方法的运行速度更快。但是,它受载荷与时间步长的影响更大。
- “广义中点”:此选项使用隐式方法求本构方程的积分。它可减少累积误差,并确保应力更新过程无条件稳定。因此,该选项更适合于复杂分析,如接触问题和重度塑性。
如果将“应力更新方法”设置为“广义中点”,则使用“广义中点参数”输入。此输入的可接受范围是 0 到 1(含)。如果将“参数”设置为等于 0,则生成的算法将是算法系列的全部显式成员(类似于“应力更新方法”的“显式”选项);但是,解并非无条件稳定。如果“参数”为 0.5 或更大,则该方法无条件稳定。如果将“参数”设置为 0.5,则求解称为中点算法;如果设置为 1,则求解称为完全 Backward Euler 或最近点算法,并采用全隐格式。值 1 比其他值更精确,对于较大的时间步尤其如此。
如果将“材料模型”(在“常规”选项卡中)设置为“各向同性”,并将“分析公式”设置为“更新拉格朗日”,则使用“应变测量”。这些选项用于改善“更新拉格朗日”方法的收敛。适用于“应变测量”的选项如下:
- “阿尔曼西应变”:(原始方法)。此选项对本构关系使用柯西应力和阿尔曼西应变,但仅限于小应变工况。
- “对数应变”:此选项对本构关系使用柯西应力和虚拟对数应变(增量应变)。它在所有工况下均可接受,包括大应变。这是一种超弹性模型,其缺点是对可压缩材料的适用性逊于不可压缩材料(泊松比 = 0.5)。原因在于,剪切模量假定为常数,但实际上它随不同的体积发生变化。
如果激活“允许重叠单元”复选框,则直线解码成单元时允许创建重叠单元。对单元进行建模时,可能必须重叠单元。这对那些局限于平面运动的问题尤其如此。
若要在分析期间的每个时间步将每个单元的应力结果写入文本日志文件,请激活“详细应力输出”复选框。这可能会导致大量输出。
如果已选择 von mises 材料模型之一,则可选择在每个时间步输出角节点和/或积分点处的当前材料状态(弹性或塑料)、当前屈服应力限制、当前等效应力限制和等效塑性应变。为此,请在“附加输出”下拉框中选择相应选项。
定义土体条件
如果选择“Duncan-Chang”材料模型,则启用“土体”选项卡。根据需要输入以下分析输入。此输入与土体的初始状态相关;有关信息,另请参见 Duncan-Chang 理论描述页面。
- 叠加静水压力:激活之后,在随附字段中输入的恒定静水压力将产生初始应力。在这种情况下,静水压力同等作用于所有方向,不要将其与随深度而增加的压力混淆。压力值必须大于 0。
- 叠加自重:激活之后,模拟土体的重量将产生初始应力。
- 表面上的参考点:指定 X、Y、Z 坐标。这是在因土体重量而产生的压力为零的情况下建立的。如果模型是土体深地的截面,则参考点可以位于模拟部件之上。
- 侧向土压力系数:大多数土体都不会产生真正的静水应力(在所有方向相等)。通常,水平方向上的应力是垂直法向应力的一部分。侧向/垂直应力之比定义侧向土压力系数。输入应介于 0 到 1 之间。
- 重力加速度:若要创建由于自重而引起的应力分布,请输入重力常数和重力作用方向以创建应力分布。该方向通常与分析中的重力作用方向相同。但是,如果模型表示初始应力的产生时间与模型的当前方向之间不同方向上的土体,则可使用不同方向。土体被移动。
定义损伤分析类型
如果“材料模型”为“正交各向异性”,且“几何类型”为“平面应力”,则将启用“损伤”选项卡。
损伤模型可模拟弹脆性正交各向异性材料的损伤出现和渐进增长情况。该模型主要用于模拟纤维增强复合材料。有关计算的其他详细信息,请参见损伤理论描述页面。
损伤模型适用于“仅材料非线性”和“完全拉格朗日”分析公式,但不适用于“更新拉格朗日”方法。
您可选择以下损伤萌生条件:
- 无:不执行任何损伤计算。
- 损伤萌生:计算部件是否发生损伤以及损伤位置,但是不计算损伤萌生后发生的情况。计算拉伸纤维准则 (fI)、压缩纤维准则 (fII)、拉伸矩阵准则 (fIII) 和压缩矩阵准则 (fIV)。
- 损伤萌生和演变:计算损伤萌生后发生的情况。发生损伤后,单元刚度缩减。除了计算得出的上述值以外,还会计算拉伸纤维损伤 (dft)、压缩纤维损伤 (d fc )、拉伸矩阵损伤 (dmt)、压缩矩阵损伤 (dmc) 和损伤能密度 (ΔED)。
- 损伤萌生和稳定演变:如果需要损伤后效应,则首选前种方法;但是,如果由于刚度骤失而发生损伤,则分析可能不稳定。选择此方法可在一定程度上增强粘性正规化 (Duvaut-Lions),从而帮助稳定求解。由于这是一种人工方法,因此应该使用获得稳定解所需的最小粘度。分析之后,将损伤能密度结果与粘性能密度结果进行比较。粘性能密度应远远小于损伤能密度,粘性效应才可忽略不计。除了计算得出的上述值以外,还会计算粘性能密度 (ΔE
V
)。选择此选项后,还将在“损伤稳定性的粘度参数”部分启用以下输入:
- 局部坐标轴 1 (拉伸):纤维拉伸模式的粘度系数 (ηft)
- 局部坐标轴 1 (压缩):纤维压缩模式的粘度系数 (ηfc)
- 局部坐标轴 2 (拉伸):矩阵拉伸模式的粘度系数 (ηmt)
- 局部坐标轴 2 (压缩):矩阵压缩模式的粘度系数 (ηmc)
使用二维单元的基本步骤
- 确保已定义单位制。
- 确保模型使用非线性分析类型。
- 对于要成为二维单元的部件,请在其“单元类型”标题上单击鼠标右键。 提示: 可用于将三维模型转换为二维模型的命令包括:“绘制”
 “图案”
“图案” “重新定位和缩放”、“绘制”
“重新定位和缩放”、“绘制” “图案”
“图案” “转动或复制”和“绘制”
“转动或复制”和“绘制”  “修改”
“修改” “投影到平面”。例如,您可能会无意中在 XY 平面中创建网格。您可以使用“重新定位和缩放”或“转动”命令将网格转动到 YZ 平面。由于舍入,某些节点的 X 坐标值可能较小,从而防止将单元类型设置为“二维”。在这种情况下,请使用“投影到平面”将节点精确捕捉到 YZ 平面。
“投影到平面”。例如,您可能会无意中在 XY 平面中创建网格。您可以使用“重新定位和缩放”或“转动”命令将网格转动到 YZ 平面。由于舍入,某些节点的 X 坐标值可能较小,从而防止将单元类型设置为“二维”。在这种情况下,请使用“投影到平面”将节点精确捕捉到 YZ 平面。 - 选择“二维”命令。
- 在“单元定义”标题上单击鼠标右键。
- 选择“编辑单元定义”命令。
- 在“常规”选项卡的“材料模型”下拉框中,选择合适的材料模式。
- 在“几何类型”下拉框中选择合适的几何类型。
- 如果在“几何类型”下拉框中选择了“平面应力”或“平面应变”选项,请输入二维单元的厚度。
- 如果选择了包含热或蠕变/粘弹性效应的材料模型,请在“热”选项卡中指定必要信息。
- 按“确定”按钮。