Analyse des chaînes de cotes 1D
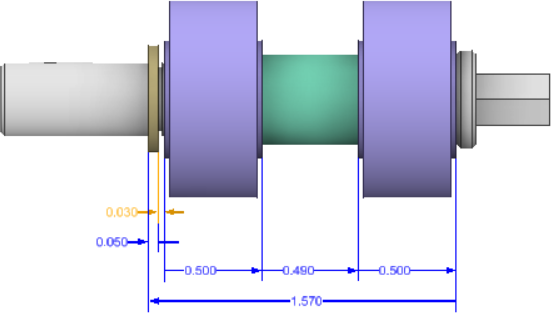
- Gérer toutes les spécifications de produit en même temps
- Utiliser les cotes et les tolérances partagées pour chaque pièce impliquée dans plusieurs chaînes de cotes
- Calculer précisément les effets des tolérances géométriques
- Inclure automatiquement les effets des dégagements autour des attaches et des broches, ce qui entraîne le basculement et la variation d'un ensemble de l'emplacement d'une pièce par rapport à une autre
- Calculer précisément les résultats statistiques
L'analyse de la tolérance d'Inventor remplace la méthode de la feuille de calcul en automatisant ces tâches et celles de la chaîne de cotes.
Concepts de base pour l'analyse de la chaîne de cotes
Les informations suivantes expliquent l'importance de l'analyse de la tolérance, les différences entre les problèmes d'analyse 1D, 2D et 3D, et les différents types d'analyse de la tolérance. Si vous connaissez déjà l'utilisation des chaînes de cotes, vous pouvez ignorer cette section et accéder directement à la rubrique Définition et modification de chaînes de cotes.
Lorsque vous concevez une pièce dans un système CAO, la représentation est parfaite. En réalité, lors de la fabrication de pièces, chaque pièce est légèrement différente. L'objectif de la conception de tolérance est de prendre en compte les variations autorisées de chaque pièce afin de déterminer si les exigences d'ingénierie sont respectées lorsque les pièces sont assemblées.
Pour déterminer le niveau de tolérance autorisé, vous devez prendre en considération l'accumulation, la chaîne de cotes ou la variation de chaque cote. Les variations dimensionnelles des pièces s'associent pour produire une variation à une distance critique, généralement entre deux différentes pièces d'un ensemble. Pour chaque distance critique, vous devez déterminer ce qui constitue une plage acceptable de valeurs dans laquelle le système fonctionne comme souhaité.
L'analyse de la chaîne de cotes permet de comprendre la relation entre la variation dimensionnelle et les exigences fonctionnelles.
L'analyse de la tolérance d'Inventor permet de résoudre les problèmes de chaîne de cotes à une dimension (1D), mais pas les problèmes de chaîne de cotes 2D et 3D. Dans de nombreux cas, l'analyse est capable de reconnaître les influences 2D ou 3D dans la chaîne de cotes définie et émet un avertissement. La section suivante définit la différence entre les chaînes de cotes 1D, 2D et 3D afin de vous aider à comprendre pourquoi le message s'affiche.
Une chaîne de cotes 1D signifie que la distance analysée et toutes les cotes contribuant à la variation de distance agissent dans la même direction linéaire. La variation linéaire des surfaces de chaque côté de la direction de la chaîne de cotes est prise en compte, mais pas la variation angulaire des surfaces relatives les unes par rapport aux autres. Parfois, les effets de la variation angulaire sont ignorés, et l'analyse est considérée comme étant en 1D. Toutefois, lorsque les surfaces de la chaîne de cotes ont des tailles drastiquement différentes, la variation angulaire sur les petites surfaces peut avoir un effet plus important que prévu sur les arêtes des plus grandes surfaces. Si ces dernières suivent l'orientation des petites surfaces, elles font des allers-retours dans la direction de l'analyse au-delà des capacités d'une translation simple des surfaces. L'analyse de la tolérance vous avertit lorsque cette situation, et d'autres avec le même effet, se produit.
Lors d'un problème de sensibilité 1D, la distance globale de la chaîne de cotes de chaque cote impliquée est égale à 1.0 ou -1.0 pour les cotes standard. La sensibilité aux cotes de taille, par exemple, au diamètre ou à la largeur, peut être 0.5 ou -0.5.
Dans la chaîne de cotes 2D, la distance est analysée et toutes les cotes qui contribuent à la variation de cette distance peuvent être représentées dans un seul plan. Une chaîne de cotes 3D peut contenir des cotes pour toutes les directions. Ces deux chaînes de cotes impliquent des calculs trigonométriques poussés qui déterminent la sensibilité des mesures de chaque cote dans l'ensemble.
Types d'analyse de la tolérance
La fonctionnalité d'analyse de la tolérance d'Inventor prend en charge les méthodes d'analyse Pire des cas, Statistique et Somme des racines carrées (RSS). La méthode d'analyse statistique RSS est un cas particulier et est décrite dans la section Statistique.
L'analyse de la tolérance Pire des cas est le type d'analyse classique pour le calcul de la chaîne de cotes. Les variables individuelles sont toutes placées aux limites maximales ou minimales pour que la distance de la chaîne de cotes soit la plus grande ou la plus petite possible.
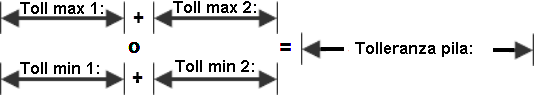
La méthode Pire des cas ne prend pas en compte la distribution des variables individuelles. Au lieu de cela, elle part du principe que toutes les pièces ont été produites à la limite maximale acceptée lorsqu'elles sont assemblées. Cette méthode permet de prévoir les limites supérieures et inférieures absolues de la distance de la chaîne de cotes qui peuvent être atteintes.
Réaliser une conception en respectant les exigences de la tolérance Pire des cas signifie que toutes les pièces produites dans leurs limites extrêmes s'assemblent et fonctionnent correctement. Le principal inconvénient de cette méthode est qu'elle nécessite des tolérances de composants individuels très précises. Cela peut causer des processus de fabrication et de contrôle très coûteux et des taux de déchets plus élevés.
Les clients exigent souvent d'assigner une tolérance qui respecte les exigences des méthodes d'analyse Pire des cas pour les interfaces mécaniques stratégiques et de remplacement des pièces de rechange. Lorsque le tolérancement Pire des cas n'est pas exigé, un tolérancement Statistique correctement réalisé peut permettre d'assurer une élasticité d'ensemble acceptable avec des tolérances de composant accrues et des coûts de fabrication faibles.
La méthode d'analyse statistique tire parti des principes statistiques pour assouplir les tolérances des composants sans sacrifier la qualité. Chaque distribution statistique est considérée comme possédant une dimension impliquée. Ces distributions sont combinées pour évaluer la distribution de la distance de la chaîne de cotes d'ensemble. L'analyse statistique prédit donc une distribution de la distance de la chaîne de cotes au lieu des limites extrêmes déterminées par la méthode Pire des cas. L'analyse statistique fournit une flexibilité de conception accrue pour la conception à un niveau de qualité quelconque, et non uniquement à cent pour cent. La différence entre l'analyse statistique et la méthode Somme des racines carrées est qu'elle ne considère pas que le niveau de qualité de l'ensemble doit être identique au niveau de qualité la pièce.
L'écart type calculé pour la distribution normale de chaque cote est calculé d'après la formule suivante pour la capacité des processus :

Résolution pour l'élasticité de l'écart type :
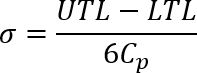
L'hypothèse la plus commune de Cp=1.0 provient de l'hypothèse d'un processus de fabrication qui place les tolérances définies à un écart type de plus ou moins 3 depuis le centre de la zone de tolérance, considéré comme la moyenne, pour que la probabilité qu'une pièce respecte les tolérances requises soit de 99,7 %. Pour les analyses statistiques, la fonctionnalité d'analyse de la tolérance part du principe que le processus de fabrication cible le milieu de la plage de tolérance, et donc que la valeur moyenne correspond à ce milieu.
L'analyse Somme des racines carrées, ou RSS, utilise les principes de la méthode d'analyse statistique générale précédemment décrite, mais en utilisant des hypothèses simplifiées afin de permettre des calculs avec des tolérances plutôt que des écarts type. L'une des principales hypothèses est que le rapport de chaque tolérance par rapport aux écarts type associés des cotes et les résultats de la chaîne de cotes sont identiques. L'analyse de la tolérance RSS utilise une capacité des processus de 1.0 pour toutes les cotes et les limites de chaîne de cotes obtenues.