Analisi della pila di tolleranza 1D
- Gestire tutti i requisiti di prodotto contemporaneamente.
- Utilizzare quote e tolleranze comuni per ciascuna parte presente in più pile.
- Calcolare con precisione gli effetti delle tolleranze geometriche.
- Includere automaticamente gli effetti delle distanze intorno a fissaggi e perni, i quali possono comportare uno spostamento dell'assieme e una variazione nel posizionamento di una parte in relazione ad un'altra parte.
- Calcolare con precisione i risultati statistici.
Analisi di tolleranza di Inventor sostituisce il metodo basato sul foglio di calcolo automatizzando queste e molte delle comuni operazioni delle pile di tolleranza.
Nozioni di base sull'analisi della pila di tolleranza
Le informazioni riportate di seguito spiegano perché l'analisi di tolleranza è importante, le differenze tra i problemi di analisi 1D, 2D e 3D e i diversi tipi di analisi della tolleranza. Gli utenti che hanno familiarità con l'esecuzione delle pile di tolleranza possono saltare questa sezione e passare direttamente a Definizione e modifica delle pile di tolleranza
La progettazione di una parte in un sistema CAD produce una rappresentazione perfetta della parte. In realtà, quando viene prodotta, ogni parte sarà leggermente diversa dalle altre. La progettazione della tolleranza consiste nel considerare la variazione consentita in ciascuna parte, in modo da determinare se i requisiti di progettazione risultano soddisfatti quando le parti vengono assemblate.
Per determinare il grado di tolleranza consentito, è necessario considerare la somma (o pila) della variazione nelle singole quote. Le variazioni di quota nelle parti si combinano per produrre la variazione in una distanza critica, in genere compresa tra due parti distinte di un assieme. Per ogni distanza critica, è necessario determinare un intervallo di valori accettabile entro il quale il sistema continua a funzionare come previsto.
L'analisi della pila di tolleranza è un modo per comprendere la relazione tra la variazione di quote e i requisiti funzionali.
Con Analisi di tolleranza di Inventor è possibile risolvere i problemi della pila unidimensionale (1D), ma non i problemi della pila 2D o 3D. Spesso, è possibile riconoscere le influenze 2D o 3D sulla pila definita e fornire un avviso all'utente. La seguente sezione indica la differenza tra pile 1D, 2D e 3D e consente di comprendere il motivo per cui il messaggio viene visualizzato.
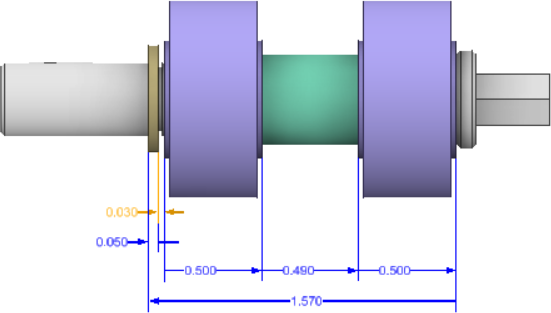
Una pila di tolleranza 1D indica la distanza che viene analizzata e tutte le quote che contribuiscono alla variazione della distanza che agiscono nella stessa direzione lineare. Viene considerata la variazione lineare delle superfici su entrambi i lati della direzione di pila; non viene considerata la variazione angolare delle superfici l'una rispetto all'altra. Talvolta gli effetti della variazione angolare vengono ignorati e l'analisi è considerata 1D. Tuttavia, laddove esistano differenze significative nella dimensione delle superfici incluse nella pila, la variazione angolare sulle superfici più piccole può avere un effetto più importante di quanto previsto sugli spigoli delle superfici più grandi. Se le superfici più grandi seguono l'orientamento delle superfici più piccole, si spostano in avanti e all'indietro nella direzione dell'analisi più di quanto sarebbe consentito dalla semplice traslazione delle superfici. Analisi di tolleranza avvisa l'utente quando rileva questo scenario e altri senari con effetti simili.
In un problema 1D, le sensibilità della distanza della pila complessiva da ciascuna quota partecipante è in genere di 1.0 o -1.0 per le quote standard. Le sensibilità per le quote dimensionali, quali diametro o larghezza, può essere di 0.5 o -0,5.
In una pila di tolleranza 2D, la distanza analizzata e tutte le quote che contribuiscono alla variazione di quella distanza possono essere rappresentate in un unico piano. La pila di tolleranza 3D può avere quote partecipanti in ogni direzione. Entrambe prevedono in genere calcoli trigonometrici complessi per determinare la sensibilità della misurazione di ciascuna quota nell'assieme.
Tipi di analisi di tolleranza
Analisi di tolleranza di Inventor supporta i metodi di analisi del caso peggiore, della statistica generale e della somma quadrati radice (RSS). L'RSS è un metodo di analisi statistica particolare ed è descritto dopo la sezione sull'analisi statistica.
L'analisi di tolleranza del caso peggiore è il tipo di calcolo della pila di tolleranza tradizionale. Le singole variabili sono portate tutte ai limiti massimo o minimo per ottenere la distanza di pila massima e minima possibile.
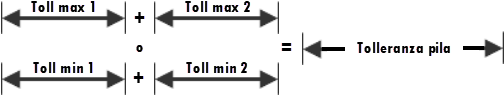
Il metodo del caso peggiore non tiene conto della distribuzione delle singole variabili. Presume invece che tutte le parti siano state prodotte al limite estremo dell'accettabile quando vengono assemblate. Questo metodo consente di prevedere i limiti superiore e inferiore assoluti della distanza di pila che è possibile realizzare.
La progettazione in base ai requisiti di tolleranza del caso peggiore implica che tutte le parti prodotte ai loro limiti estremi (ma non oltre) possono essere assemblate e funzionano correttamente. Il principale svantaggio del metodo del caso peggiore è che spesso richiede tolleranze ridotte per i singoli componenti. Questo può avere come risultato processi di produzione e ispezione costosi e un'elevata percentuale di scarti.
Spesso viene richiesto di assegnare una tolleranza che soddisfi i metodi di analisi del caso peggiore per le interfacce meccaniche critiche e le interfacce di sostituzione delle parti di ricambio. Quando la tolleranza del caso peggiore non è un requisito contrattuale, una tolleranza statistica adeguatamente applicata garantisce risultati di assieme accettabili, con tolleranze di componente più flessibili e costi di produzione inferiori.
Il metodo di analisi statistica sfrutta i principi della statistica per distendere le tolleranze di componente senza compromettere la qualità. Presume che ogni quota partecipante abbia una distribuzione statistica. Queste distribuzioni sono combinate per prevedere la distribuzione della distanza di pila dell'assieme. L'analisi statistica è in grado di prevedere una distribuzione della distanza di pila, anziché i limiti estremi come per il metodo del caso peggiore. L'analisi statistica offre una maggiore flessibilità di progettazione a qualsiasi livello di qualità, non soltanto al 100%. L'analisi statistica differisce dal metodo RSS poiché non presuppone che il livello di qualità dell'assieme sia lo stesso del livello di qualità della parte.
La deviazione standard calcolata per la distribuzione normale di ogni quota viene calcolata in base alla seguente formula per Cp:

Risoluzione per i risultati di deviazione standard:
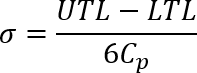
Il presupposto più comune di Cp=1.0 deriva dal presupposto di un processo di produzione ove le tolleranze definite sono posizionate a deviazioni standard di +/- 3 dal centro della zona di tolleranza, la quale è considerata la media; in questo modo, la probabilità che una parte soddisfi le tolleranze richieste è pari al 99,7%. Per tutte le analisi statistiche, Analisi di tolleranza presume che la produzione miri al punto medio dell'intervallo di tolleranza; pertanto, la media è considerata il punto medio dell'intervallo di tolleranza.
L'analisi della somma quadrati radice (RSS) è basata sui principi del metodo di analisi statistica generale descritto nella sezione precedente, ma con alcuni presupposti semplificativi che permettono i calcoli con le tolleranze, al posto delle deviazioni standard. Uno dei presupposti principali è che i rapporti di ciascuna tolleranza rispetto alle deviazioni standard associate sulle quote e il risultato di pila siano uguali. In un'analisi RSS, Analisi di tolleranza presume un Cp di 1.0 per tutte le quote e per i limiti di pila risultanti.