Para definir os parâmetros de análise modal para novos casos dinâmicos na estrutura, execute um dos seguintes procedimentos:
- Selecione um caso de análise modal na caixa de diálogo Novo caso e clique em OK.
- Selecione um caso de análise modal na caixa de diálogo Tipo de análise e clique em Definir parâmetros.
Recomenda-se aplicar um solver iterativo para resolver problemas em larga escala, pois ele fornece três métodos para resolver problemas de valor próprio. Para fazer isso, selecione Solver iterativo na caixa de diálogo Análise estrutural em Preferências do trabalho.
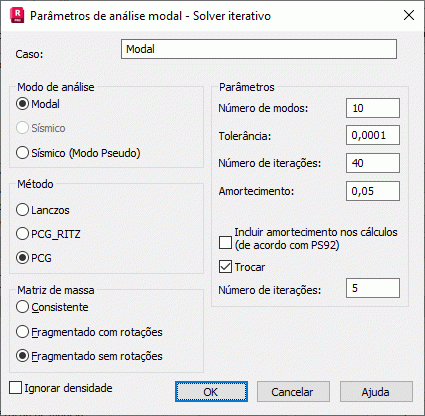
Modo de análise
Atualmente, os modos modal e sísmico (pseudo) estão disponíveis para o solver iterativo. O modo modal somente está acessível para o gradiente conjugado pré-condicionado (PCG) [1-4]. O modo sísmico (pseudo) está acessível para o Lanczos modificado e gradiente de Ritz(PCG_Ritz).
Método
Método de Lanczos
Lanczos é um Método de Lanczos modificado que evita a fatoração de uma matriz em larga escala. O gradiente conjugado pré-condicionado (PCG) gera uma coleção de vetores de Lanczos em vez de executar novamente a resolução da matriz de rigidez fatorada. Todos os tipos de pré-condicionamento definidos para análise estática estão disponíveis (Ferramentas > Preferências do trabalho > Iterativo > Parâmetros).
O Lanczos modificados é preferível na análise sísmica e espectral de estruturas grandes quando muitos modos são necessários.
- Parâmetros requeridos
Tipo de matriz de massa (fragmentada com rotações ou consistente) e número de modos.
A precisão do cálculo depende da tolerância presumida de cálculo de vetores de Lanczos e do Número de modos. A tolerância é atribuída em Ferramentas > Preferências do trabalho > Iterativo > Parâmetros e é a mesma dos casos estáticos. A tolerância na caixa de diálogo Parâmetros de análise modal – Solver iterativo indica uma tolerância para uma solução de um problema de valor próprio generalizado, incluindo vetores de Lanczos definidos e não pode ser menor que 1,0e-04.
Quanto maior o Número de modos, mais próximos os vetores de Ritz baixos estarão dos valores próprios adequados. A soma das massas modais será mais exata.
PCG_Ritz
PCG_Ritz é um método de Ritz no qual a abordagem de gradiente pré-condicionado é usada para gerar uma coleção de vetores de base (método gradiente de Ritz [5]). O método PCG_Ritz é preferível para definições rápidas aproximadas de pares próprios durante a análise sísmica e espectral. É necessário selecionar um método de vários níveis. Também é recomendável atribuir um nível de agregação. Esse método será eficaz para problemas de médio porte (até 60.000 equações). Todos os tipos de pré-condicionamento definidos para análise estática estão disponíveis (Ferramentas > Preferências de trabalho > Iterativo > Parâmetros).
- Parâmetros necessários
Tipo de matriz de massa (fragmentada com rotações ou consistente) e número de modos. A precisão dos cálculos depende do Número de modos.
PCG
PCG é um método de gradiente conjugado pré-condicionado [1-5] que é preferível quando um pequeno número de modos próprios é definido. Por exemplo, o método PCG pode se revelar muito útil ao aplicar cargas de vento ou ao verificar um pequeno número de modos baixos obtidos por meio do método PCG_Ritz. Todos os tipos de pré-condicionamento definidos para análise estática estão disponíveis (Ferramentas > Preferências de trabalho > Iterativo > Parâmetros). Todos os tipos de matriz de massa (consistente, fragmentado com rotações, fragmentado sem rotações) podem ser aplicados.
- Parâmetros necessários:
Número de modos; Tolerância – critérios de precisão relativos a iterações de interrupção; Número de iterações – número máximo permitido de iterações para cada modo (o processo de iteração para cada modo será interrompido, se um parâmetro de tolerância atual for menor que a Tolerância ou se um número de iterações atual exceder o Número de iterações); Deslocamento – aproveita a técnica de mudança para a aceleração de convergência; Número de repetições – determina um número de repetições (para cada modo o algoritmo executa iterações determinadas pelo número de iterações, corrige um valor de deslocamento e repete as iterações determinadas pelo número de iterações pelo número de vezes definido pelo Número de repetições).
- Parâmetros recomendados:
Método multinível ou não multinível com abordagem ICCF (Ferramentas > Preferências do trabalho > Iterativo > Parâmetros); nModos £ 5; Tolerância = 0,01; Número de iterações = 100 para um método não multinível; Deslocamento – desativado
- Tipo de matriz de massa.
- Parâmetros (número de modos, tolerância, número de iterações, amortecimento).
- Deslocamento (com o número de iterações).
Evitar configurações incorretas do solver iterativo
Um sistema de controle evita configurações incorretas de parâmetros de análise modal para solvers iterativos. Ele é ativado quando o botão OK é clicado para iniciar a análise modal. Um prompt de parâmetros de análise é exibido. Clique em Sim para aceitar os valores de parâmetro determinados na caixa de diálogo. Clique em Não para retornar à caixa de diálogo Parâmetros de análise modal e fazer correções.
Se um solver iterativo no modo Sísmico (Pseudo) for usado em cálculos, faça o seguinte.
- O número de níveis de agregação deve ser igual a 1 (Preferências do trabalho > Estrutura de análise/Parâmetros > Iterativo)
- O número do modo pesquisado deve ser inserido com valor pelo menos três vezes maior que o necessário.
- Uma convergência de solução deve ser verificada quanto ao número do modo apresentado no ponto 2 e um número de modo duas vezes maior. Se houver falta de convergência (valores próprios claramente diferentes para o número do modo duas vezes maior que para o número inicial), o número de modos deverá ser aumentado. Uma vez obtida a solução convergente, a filtragem de modo pode ser aplicada para limitar o número do modo.
Para um tipo de análise desse tipo, o parâmetro Tolerância nos resultados da análise dinâmica não tem significado prático e pode ser ignorado. Se essas recomendações não forem seguidas, o erro poderá atingir uma porcentagem com valor de várias dezenas.
Referências
- Gambolati G., Pini G., Sartoretto F., An improved iterative optimization technique for the leftmost eigenpairs of large symmetric matrices, J. Comp. Phys., 74: 41 – 60, 1988.
- Sartoretto F., Pini G., Gambolati G., Accelerated simultaneous iterations for large finite element eigenproblems, J. Comp. Phys., 81: 53 – 69, 1989.
- Papadrakakis. A partial preconditioned conjugate gradient method for large eigenproblems, Comp. Meth. Appl. Mech. Eng., 62: 195 – 207, 1987.
- M.Papadrakakis, Solving large -scale problems in mechanics, John Wiley & Sons Ltd., 1993.
- Fialko S., High-performance aggregation element-by-element Ritz-gradient method for structure dynamic response analysis, CAMES, 7: 537-550, 2000.
Consulte também:
Parâmetros de análise modal que reconhecem forças estáticas
Descrição da análise modal que reconhece forças estáticas
Descrição do método de iteração de subespaço do bloco
Análise modal – Precisão dos cálculos