Solvers iterativos

Há vários tipos de solvers iterativos.

ICCF iterativo

Esse método é recomendado para problemas de larga escala com um pequeno número de laterais direitas.

• Uso de memória: alto.
• Uso de disco: não usado.
• Estimativa de velocidade: rápida (para problemas bem condicionados).
• Quantidade de equações: 15.000 – 1.000.000 equações e mais.
• Análises suportadas: estáticas lineares, análise modal, flambagem.
• Limitações de análise disponíveis: N/D.
• Outras limitações:
  • Não é verificada a correção das restrições de estrutura.
  • Convergência lenta se alguns problemas estiverem incorretamente condicionados.

Diagonal iterativa

Esse método é recomendado para problemas de larga escala com um pequeno número de laterais direitas.

• Uso de memória: mínimo
• Uso de disco: mínimo
• Estimativa de velocidade: baixa
• Quantidade de equações: 15.000 – 1.000.000 equações e mais.
• Análises suportadas: estáticas lineares, análise modal, flambagem.
• Limitações de análise disponíveis: N/D.
• Outras limitações:
  • Não é verificada a correção das restrições de estrutura.
  • Convergência lenta se alguns problemas estiverem incorretamente condicionados.

Gauss-Cholesky iterativo

Esse método é recomendado para problemas de larga escala com um pequeno número de laterais direitas, quando não há RAM suficiente para usar o método ICCF.

A verificação de cada matriz de elemento é realizada por meio do procedimento de regularização de Vinget ¹².

• Uso de memória: mínimo
• Uso de disco: mínimo
• Estimativa de velocidade: baixa
• Quantidade de equações: 15.000 – 1.000.000 equações e mais.
• Análises suportadas: estáticas lineares, análise modal, flambagem.
• Limitações de análise disponíveis: N/D.
• Outras limitações:
  • Não é verificada a correção das restrições de estrutura.
  • Convergência lenta se alguns problemas estiverem incorretamente condicionados.

ICCF multinível iterativo

Esse método é recomendado para problemas de larga escala com um pequeno número de laterais direitas. Ele apresenta uma convergência mais rápida do que o método ICCF iterativo.

• Uso de memória: alto
• Uso de disco: mínimo
• Estimativa de velocidade: rápida para problemas bem condicionados
• Quantidade de equações: 15.000 – 1.000.000 equações e mais.
• Análises suportadas: estáticas lineares, análise modal, flambagem.
• Limitações de análise disponíveis: tipos de estrutura disponíveis: 3D (barra, casca, sólido e todos os elementos finitos especiais), estrutura 2D.
• Outras limitações:
  • Não é verificada a correção das restrições de estrutura.
  • Convergência menos estável em alguns casos.

Diagonal iterativa multinível

Esse método é consideravelmente mais lento do que o ICCF multinível iterativo. No entanto, exige muito menos memória RAM.

O método de Suavização 2 normalmente exige menos iterações em comparação com o método ICCF multinível iterativo.

A verificação de cada matriz de elemento é realizada por meio do procedimento de regularização de Vinget ^1,2.

• Uso de memória: mínimo
• Uso de disco: mínimo
• Estimativa de velocidade: baixa
• Quantidade de equações: 15.000 – 1.000.000 equações e mais.
• Análises suportadas: estáticas lineares, análise modal, flambagem.
• Limitações de análise disponíveis: tipos de estrutura disponíveis: 3D (barra, casca, sólido e todos os elementos finitos especiais), estrutura 2D.
• Outras limitações:
  • Não é verificada a correção das restrições de estrutura.

Gauss-Cholesky iterativo e multinível

Esse método é consideravelmente mais lento do que o ICCF multinível iterativo. No entanto, exige muito menos memória RAM.

O método de Suavização 2 normalmente exige menos iterações em comparação com o método ICCF multinível iterativo.

A verificação de cada matriz de elemento é realizada por meio do procedimento de regularização de Vinget ^1,2.

• Uso de memória: mínimo
• Uso de disco: mínimo
• Estimativa de velocidade: média (para problemas bem condicionados)
• Quantidade de equações: 15.000 – 1.000.000 equações e mais.
• Análises suportadas: estáticas lineares, análise modal, flambagem.
• Limitações de análise disponíveis: tipos de estrutura disponíveis: 3D (barra, casca, sólido e todos os elementos finitos especiais), estrutura 2D.
• Outras limitações:
  • Não é verificada a correção das restrições de estrutura.

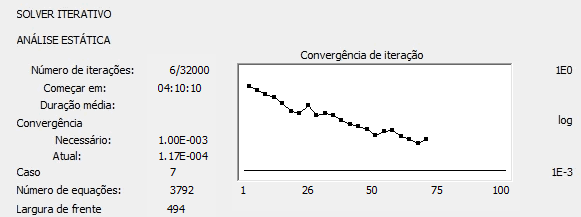
Cálculos do método iterativo

A caixa de diálogo de cálculos do método iterativo mostrará o processo de convergência do método iterativo se o nível de precisão definido pelo usuário for alcançado ou se o processo for divergente.

O diagrama também mostra as seguintes informações:

• Número da iteração atual/número máximo de iterações.
• Precisão necessária.
• Precisão da iteração atual.
• Número de equações.
• Largura de frente.