O método de iteração de subespaço do bloco é recomendado para o cálculo de estruturas grandes com uma quantidade excessiva de modos a serem calculados.
Os métodos de iteração de subespaço resolvem o sistema de equações de problemas de valor próprio Kφ - λBφ = 0.
Normalmente, esse método é mais rápido do que o método de Lanczos.
A tolerância (convergência necessária) da solução de problema próprio é determinada pela fórmula:
![]()
O parâmetro de tolerância (tol) é definido na caixa de diálogo Parâmetros de análise modal. A precisão dos cálculos pode ser aumentada ao reduzir o valor de tolerância tol. Isso resulta no aumento do número de iterações.
Cálculos
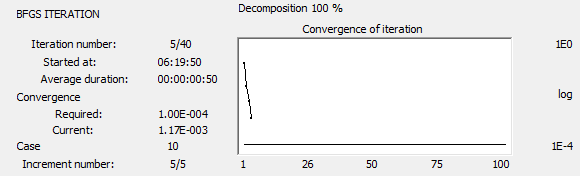
A caixa de diálogo de cálculos para o Método de iteração de subespaço mostra as seguintes fases:
- Número da iteração atual/número máximo de iterações.
- Precisão necessária (tolerância).
- Precisão da iteração atual.
- Número de modos necessários.
Consulte também: