Bifrost includes basic nodes and data types for dealing with transformations like scaling, rotation, and translation. These include vectors, matrices, and quaternions of type float amd double.

• 3D vectors are often used to represent positions, translation offsets, and normals. They can also be used to represent non-uniform scaling factors, as well as other triples like color values.
• Matrices are mathematical structures that can represent transformations.
  • 3×3 matrices can represent combined scaling and rotation.
  • 4×4 matrices can represent scaling, rotation, and translation using homogeneous coordinates.
• Quaternions are 4D vectors that can represent rotation if they are normalized. In Bifrost, the components are XYZW with the real component W in the last place.

Multiply matrices and vectors

Use the matrix_multiply node to multiply matrices, as well as to multiply matrices and vectors. Using the regular multiply node with matrices yields the element-wise product instead of the matrix product, similar to the Python NumPy library.

Bifrost uses column vectors — this means that to multiply a matrix and a vector, the matrix is first and the vector is last (post-multiplied). If p is a position with respect to an object's reference frame, L is the object's local transform matrix, and W is the object's parent's world transform matrix, then the position in world coordinates is given by:

W × L × p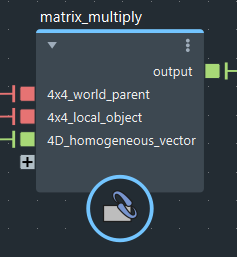

When implementing formulas from sources that use row vectors, you need to reverse the order of multiplication. You may also need to transpose the matrices, if they haven't been transposed already — matrix inputs and outputs to and from the host scene are automatically transposed if necessary.

Compose and decompose matrices

Use the SRT_to_matrix compound to create a matrix based on:

• A 3D vector (float or double-precision) of possibly non-uniform scaling factors in XYZ. If you want to force the scaling to be uniform, connect a single value that gets promoted to 3D vector.
• A quaternion (4D vector) representing a rotation. The input is automatically normalized to represent a rotation in 3D.
• A 3D vector for the translation.

The output of SRT_to_matrix is a 4×4 matrix, suitable for multiplying a vector in homogeneous coordinates. To convert a 3D vector to homogeneous coordinates and back, use vector3_to_vector4 and vector4_to_vector3 — set the input w to 1 to transform as a position or to 0 to transform as length and direction only.

Alternatively, if you require a 3×3 matrix, explode SRT_to_matrix and use the output of the matrix_multiply node.

The order of operations is scaling first, then rotation, and finally translation. If these operations were represented by separate matrices S, R, and T, then the mathematical order of operations is:

T × R × S × p

To convert the other way, use matrix_to_SRT to break a matrix apart into its constituent scale, rotation, and translation. The transform input is a 4×4 matrix, but you can still connect a 3×3 matrix (in which case, the translation output is always the zero vector). Note that shear and perspective are not considered — if these are present in the matrix, then the results will be incorrect.

Construct and deconstruct matrices

Use value nodes to construct or deconstruct a matrix based on its individual columns and values.

1. In the parameter editor, click More (...) and select a matrix type.
2. Use the +/– icons on the ports to access its elements.