Fiber breakage model for long-fiber composites
The option to calculate fiber breakage when performing a fiber orientation analysis using a long-fiber composite material has been implemented.
The fiber breakage model implemented was first proposed by Phelps and Tucker [1] as a statistical model which describes the probability of a fiber breaking due to buckling and shearing forces in a flow field.
A fiber buckles and breaks under the hydrodynamic compression force, described by Dinh and Armstrong [2]. The probability of breaking under the hydrodynamic forces can be expressed as:
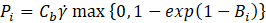
and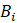 
is determined by the ratio of the actual fiber length to the unbreakable length 
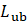[3]
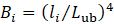
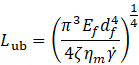
where other variables are the properties of the fiber and matrix, except for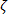 
which is the drag factor.
The fibers, broken or not, have to follow a conservation law because they cannot disappear nor can they grow in a flow field. This conservation law can be expressed as:
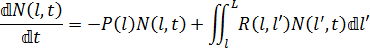
where L is the initial fiber length, N(l,t) is number of fibers with length l at time t, P(l)is the scalar probability function of fiber length l, and R(l,l') is the probability function of fiber length l breaking to form a fiber of length l' (where l'<\l). It can be expressed as a Gaussian breakage profile, such as:
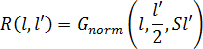
where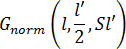 
is the Gaussian normal probability density function for the variable l with mean l'/2 and standard deviation Sl'. S is a dimensionless fitting parameter that can be used to control the shape of the Gaussian breakage profile.
References
- Phelps, J.H., Processing-microstructure Models for Short- and Long-fiber Thermoplastic Composites. Ph.D. thesis, University of Illinois at Urbana-Champaign (2009).
- Dinh, S.M. and Armstrong, R.C., A Rheological Equation of State for Semi-Concentrated Fiber Suspensions. J. Rheol., 28(3):207-227 (1984).
- Phelps, J.H., Abd El-Rahman, A.I, Kunc, V. and Tucker, C.L, A Model for Fiber Length Attrition in Injection-Molded Long-Fiber Composites. Composites Part A: Applied Science and Manufacturing, 51:11-21 (2013).