Thermal stress 01: hollow cylinder with thick walls and temperature gradient
A thick-walled cylindrical vessel under uniform logarithmic temperature gradient throughout the thickness is analyzed for thermal stress.
Case Description
The model is an eighth-symmetry representation of the cylinder. There is a temperature difference of ΔT between the outside face and the inside face of the cylinder, with the inside face colder than the outside face. The ends of the cylinder are not constrained. The solution is valid away from the ends of the cylinder. The internal temperature distribution is logarithmic throughout the thickness (that is, a steady-state temperature distribution). For this example, an outside radius of 2" and an inside radius of 1" were used with a temperature difference of 10˚F.
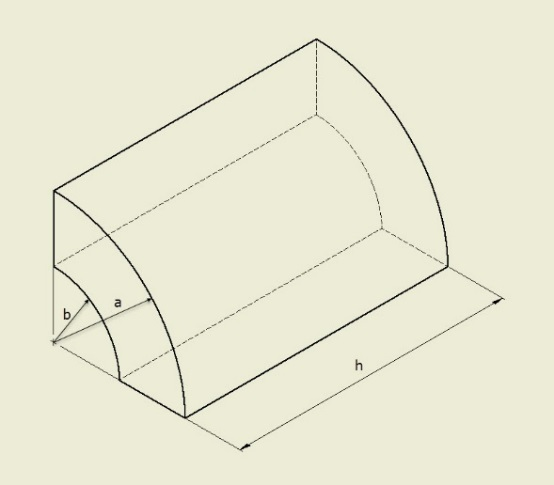
Dimensions
- a = 2 inches
- b = 1 inch
- h = 4 inches
Study Type
- Thermal Stress
Mesh Parameters
- Mesh Type = Solid, Tetrahedral
- Mesh Size = 0.2 inch, absolute
- Element Order = Parabolic
- Adaptive Mesh Refinement: None
Material Properties
- Modulus of Elasticity = 3 X 107 psi
- Poisson's ratio (v) = 0.3
- Coefficient of Thermal Expansion (α) = 6 x 10-6/°F
Constraints
- Frictionless Constraints at the following three faces:
- Face that lies in the XY plane (at the -Z end of the model)
- Face that lies in the YZ plane
- Face the lies in the XZ plane
Loads
- Applied Temperature at inner face of the cylinder = -10° F
- Applied Temperature at outer face of the cylinder = 0° F
Comparison of Results
Normal YY Stress Tensors (psi) at the two corners indicated in the following image. These corners are at the intersection of two planes of symmetry. Therefore, they represent points mid-way along the length of the full cylinder, well removed from the open ends. The Normal YY Stress corresponds to the tangential (hoop) stress of the cylinder.
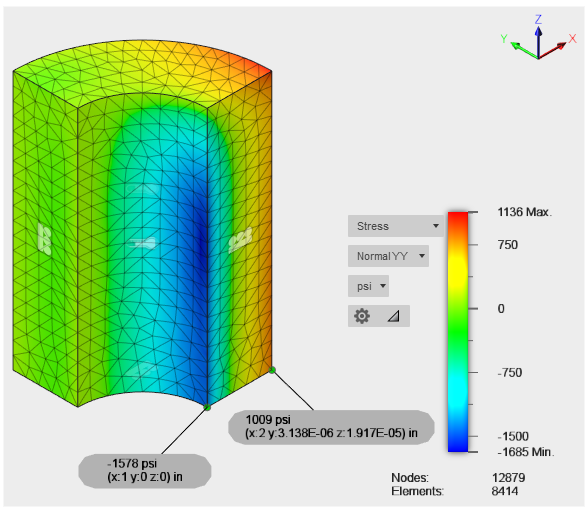
| Location | Roark and Young | Fusion | % Difference |
|---|---|---|---|
| Inner Corner | -1574 psi | -1578 psi | 0.25 % |
| Outer Corner | 998 psi | 1009 psi | 1.10 % |
Reference
Roark, R. J. and Young, W. C., Roark's Formulas for Stress and Strain, Fifth Edition, New York: McGraw-Hill, 1975, page 585, Section 15.6, Case 16.
