Um diesen Prozess weiter zu verfeinern, kann auch eine Standardfehlerellipse gezeichnet werden. Mit einer F-Verteilung aus den angewendeten Statistiken wird eine Fehlerellipse mit einer 95%igen oder einer 99%igen Wahrscheinlichkeit erstellt. Die Ellipse verfügt über Bogen, die die Seiten des Fehlerrechtecks berühren; die Ausrichtung wird durch einen Winkel (t) und rechtwinklige U-V-Hilfsachsen bestimmt. Auch hier werden Werte von der Kovarianzmatrix herangezogen, um den Winkel t sowie die zugehörige große und kleine Halbachse zu berechnen.
Bestimmen Sie zunächst drei Variablen, die in Gleichungen verwendet werden sollen, die die große und kleine Halbachse ermitteln: K, Quu und Qvv.
Die folgenden Formeln werden verwendet:
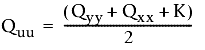
und
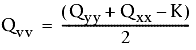
Dabei gilt
- Qxx, Qyy und Qxy sind Werte aus der Kovarianzmatrix.
Anhand dieser Werte werden dann zwei Gleichungen zur Bestimmung von Su, der Länge der großen Halbachse, und Sv, der Länge der kleinen Halbachse, aufgestellt:
und
Dabei gilt
- So = Standardabweichung der Gewichtung
Der Winkel t, der von der U- und der Y-Achse gebildet wird, wird durch folgende Gleichung bestimmt:
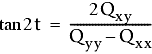
Der angepasste Punkt befindet sich mit einer 95%igen oder einer 99%igen Wahrscheinlichkeit innerhalb dieser Ellipse.