Расчет поведения конструкции во времени позволяет определить реакцию конструкции на определенное воздействие нагрузки в заданные моменты времени в отличие от других типов анализа, используемых в Robot, которые показывают реакцию конструкции в форме амплитуд, полученных для отдельного момента.
Исследование поведения конструкции во времени состоит в нахождении решения следующего уравнения относительно переменных, зависящих времени t
M * a(t) + C * v(t) + K * d(t) = F(t)
где известны следующие исходные значения: d(0) =d0 и v(0) =v0,
где
M - матрица масс;
K - матрица жесткости;
C = a * M + b * K - матрица затухания;
α - коэффициент, определенный пользователем;
β - коэффициент, определенный пользователем;
d - вектор перемещения;
v - вектор скорости;
a - вектор ускорения;
F - вектор нагрузки.
Все выражения, содержащие параметр t, зависят от времени.
Для решения задачи программа использует метод Ньюмарка или метод декомпозиции. Метод Ньюмарка относится к группе алгоритмов, которые безусловно сходятся при задании определенных параметров. Для вычисления перемещений и скорости на следующем шаге интегрирования метод использует следующие формулы:
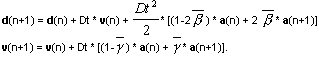
Параметры β и γ контролируют сходимость и точность результатов, полученных с помощью данного метода.
Безусловная сходимость обеспечивается для 0.5 ≤ γ 2≤* b.
В программе по умолчанию принимаются следующие два значения параметров: b = 0,25 и g = 0,5. Изменять эти величины можно только в том случае, когда используется расчет колебаний с активизированным методом Ньюмарка или Ньюмарка (ускорение). Эти величины (параметры TransBeta и TransGamma) можно изменить в файле настроек *.COV, сохраненном в папке CFGUSR; для выполнения расчета для различных величин параметров b и g, необходимо изменить параметры TransBeta и TransGamma в файле *.COV, а затем загрузить этот файл настроек в Robot.
Метод Ньюмарка целесообразно использовать для исследования поведения конструкции под воздействием сосредоточенной нагрузки в течение короткого времени. Такие нагрузки вызывают движения, для описания которых требуется большое количество собственных форм. Поэтому для этого типа задач метод Ньюмарка более эффективен, чем метод разложения по формам. Метод Ньюмарка использует начальные уравнения без каких-либо упрощений. Точность полученных результатов зависит от точности численного интегрирования временной формулы, и определяется значением временного шага для выбранных параметров α, β. Метод не требует определения собственных значений и собственных векторов. Тем не менее, при исследовании длительных процессов данный метод требует больших затрат времени, поскольку для достижения необходимой точности такие расчеты должны быть выполнены с использованием большого количества шагов по времени.
Метод Гильбера-Хьюджеса-Тэйлора (HHT) позволяет осуществлять многочисленные демпфирования высокой частоты, сохраняя при этом точность решения. Дискретная форма уравнения колебаний выглядит следующим образом:
где
-1/3 ≤ α ≤ 0
Принимая:
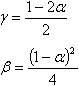
получается безусловно устойчивая схема интегрирования с точностью второго порядка.
Для формы ускорения, ‘пробнойґ величины на n+1 шаге интегрирования определяются следующим образом:
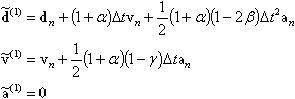
Метод HHT является очень эффективными алгоритмом для числового интегрирования, который позволяет устранить неблагоприятное влияние высоких частот на качество решения.
Метод разложения по формам является более простым методом достижения требуемого результата. Этот метод основан на представлении движения конструкции в виде суперпозиции движения отдельных форм. Поэтому метод требует определения собственных значений и собственных векторов. Для этой цели рекомендуется использовать метод Ланцоша, который должен следовать за проверкой Штурма. Метод разложения по формам использует разделенные сокращенные уравнения.
Уравнение без учета затухания принимает следующую форму:
, где
![]() ,
,
Ng – число "групп нагрузки", φk(t) – история процесса для k-той группы нагрузки;
![]() (2)
(2)
После подстановки уравнения (2) в уравнение (1), а также задания затухания формы и условий ортогональности ![]() , получаем следующее уравнение:
, получаем следующее уравнение:
где ![]() , ξ - параметр затухания формы, ωi – частота i-той формы.
, ξ - параметр затухания формы, ωi – частота i-той формы.
Каждое уравнения решается численно с точностью второго порядка. Результирующий вектор смещения X(t) для определения временных точек t* = t1, t2, ..., получен после введения qi (t*), i=1,2,..., m в формулы (2).
Гораздо более важные различия существуют между расчетом колебаний и близкими к нему типами расчета. Так тип расчета "Временная нагрузка" в принципе отличается от типа расчета "Колебаний" тем, что первый тип исследований не учитывает динамических эффектов. Различие между Гармоническим анализом и "Анализом во времени" состоит в том, что первый тип анализа определяет реакцию конструкции исключительно в форме амплитуд, в то время как второй тип расчета представляет результат в виде функций времени.
См. также: