Для дальнейшего уточнения этого процесса можно построить эллипс среднеквадратической ошибки. Эллипс ошибки с вероятностью 95% или 99% создается с помощью F-распределения применяемых статистических данных. Дуги эллипса являются касательными к сторонам прямоугольника ошибки, его ориентация определяется углом t и дополнительными ортогональными осями u-v. Значения из ковариационной матрицы используются для вычисления угла t и соответствующих большой и малой полуосей.
Сначала вычислим три переменных для использования в уравнениях, определяющих большую и малую оси: K, Quu и Qvv.
Используются формулы:
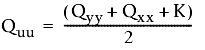
и

где:
- Qxx, Qyy и Qxy - значения из ковариационной матрицы.
Затем полученные значения используются для решения двух уравнений и определения Su - длины большой полуоси, и Sv - длины малой полуоси:
и
где:
- So = среднеквадратическое отклонение весового коэффициента единиц
Наконец, по следующей формуле вычисляется угол t между осями u и Y:
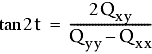
Скорректированная точка вероятнее всего находится в пределах этого эллипса со степенью достоверности 95% или 99%.