Pro další zpřesnění procesu je možné nakreslit také standardní chybovou elipsu. Pomocí distribuce F z aplikované statistiky se vytvoří buď 95%, nebo 99% pravděpodobnostní chybová elipsa. Tato elipsa má tečny oblouků ke stranám chybového obdélníku s orientací, která je určena úhlem t a pomocnými ortogonálními osami u-v. Hodnoty z kovarianční matice se opět použijí pro výpočet úhlu t a související hlavní a vedlejší poloosy.
Nejprve vyřešte tři proměnné v rovnici, které určují hlavní a vedlejší poloosu: K, Quu a Qvv.
Použijí se tyto rovnice:
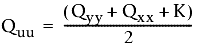
a
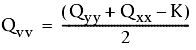
kde
- Qxx, Qyy a Qxy jsou hodnoty z kovarianční matice.
Dále se tyto hodnoty použijí k vyřešení dvou rovnic za účelem určení délky hlavní poloosy Su a délky vedlejší poloosy Sv:
a
kde
- So = směrodatná odchylka jednotkové váhy
Nakonec se pomocí následující rovnice vyřeší úhel t, který svírají osa u a osa Y:
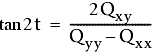
Upravený bod se s největší pravděpodobností nalézá v rámci této elipsy s 95% nebo 99% úrovní spolehlivosti.